|
Kochanek–Bartels Spline
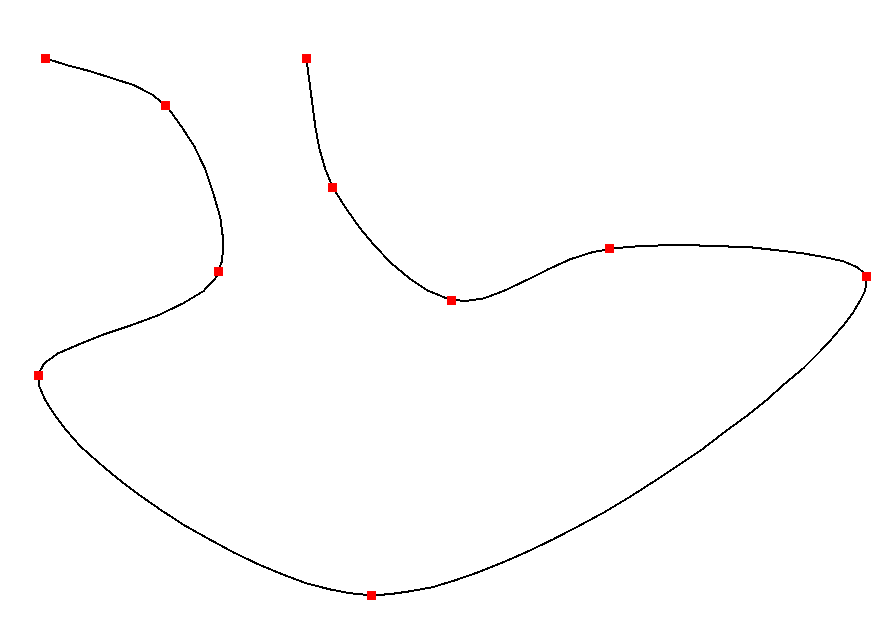
In mathematics, a Kochanek–Bartels spline or Kochanek–Bartels curve is a cubic Hermite spline with tension, bias, and continuity parameters defined to change the behavior of the tangents. Given ''n'' + 1 knots, :p0, ..., p''n'', to be interpolated with ''n'' cubic Hermite curve segments, for each curve we have a starting point p''i'' and an ending point p''i''+1 with starting tangent d''i'' and ending tangent d''i''+1 defined by :\mathbf_i = \frac(\mathbf_i-\mathbf_) + \frac(\mathbf_-\mathbf_i) :\mathbf_ = \frac(\mathbf_-\mathbf_) + \frac(\mathbf_-\mathbf_) where... Setting each parameter to zero would give a Catmull–Rom spline. Thsource code found hereof Steve Noskowicz in 1996 actually describes the impact that each of these values has on the drawn curve: The code includes matrix summary needed to generate these splines in a BASIC BASIC (Beginners' All-purpose Symbolic Instruction Code) is a family of general-purpose, high-level programming languages des ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Kochanek Bartels Spline
Christopher Kochanek is an American astronomer. He works in the fields of cosmology, gravitational lensing, and supernovae. Kochanek currently is an Ohio Eminent Scholar at Ohio State University as well as an Elected Fellow of the American Association for the Advancement of Science. In 2020, he was the recipient of the Beatrice M. Tinsley Prize with Krzysztof Stanek for their leadership of the All-Sky Automated Survey for Supernovae ASAS-SN), in addition to the Dannie Heineman Prize for Astrophysics The Dannie Heineman Prize for Astrophysics is jointly awarded each year by the American Astronomical Society and American Institute of Physics for outstanding work in astrophysics Astrophysics is a science that employs the methods and princi .... References Year of birth missing (living people) Living people Fellows of the American Association for the Advancement of Science Ohio State University faculty American astronomers California Institute of Technology alumni ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mathematics
Mathematics is an area of knowledge that includes the topics of numbers, formulas and related structures, shapes and the spaces in which they are contained, and quantities and their changes. These topics are represented in modern mathematics with the major subdisciplines of number theory, algebra, geometry, and analysis, respectively. There is no general consensus among mathematicians about a common definition for their academic discipline. Most mathematical activity involves the discovery of properties of abstract objects and the use of pure reason to prove them. These objects consist of either abstractions from nature orin modern mathematicsentities that are stipulated to have certain properties, called axioms. A ''proof'' consists of a succession of applications of deductive rules to already established results. These results include previously proved theorems, axioms, andin case of abstraction from naturesome basic properties that are considered true starting poin ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Cubic Hermite Spline
In numerical analysis, a cubic Hermite spline or cubic Hermite interpolator is a spline where each piece is a third-degree polynomial specified in Hermite form, that is, by its values and first derivatives at the end points of the corresponding domain interval. Cubic Hermite splines are typically used for interpolation of numeric data specified at given argument values x_1,x_2,\ldots,x_n, to obtain a continuous function. The data should consist of the desired function value and derivative at each x_k. (If only the values are provided, the derivatives must be estimated from them.) The Hermite formula is applied to each interval (x_k, x_) separately. The resulting spline will be continuous and will have continuous first derivative. Cubic polynomial splines can be specified in other ways, the Bezier cubic being the most common. However, these two methods provide the same set of splines, and data can be easily converted between the Bézier and Hermite forms; so the names are o ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Tangent
In geometry, the tangent line (or simply tangent) to a plane curve at a given point is the straight line that "just touches" the curve at that point. Leibniz defined it as the line through a pair of infinitely close points on the curve. More precisely, a straight line is said to be a tangent of a curve at a point if the line passes through the point on the curve and has slope , where ''f'' is the derivative of ''f''. A similar definition applies to space curves and curves in ''n''-dimensional Euclidean space. As it passes through the point where the tangent line and the curve meet, called the point of tangency, the tangent line is "going in the same direction" as the curve, and is thus the best straight-line approximation to the curve at that point. The tangent line to a point on a differentiable curve can also be thought of as a ''tangent line approximation'', the graph of the affine function that best approximates the original function at the given point. Similarly ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Spline (mathematics)
In mathematics, a spline is a special function defined piecewise by polynomials. In interpolating problems, spline interpolation is often preferred to polynomial interpolation because it yields similar results, even when using low degree polynomials, while avoiding Runge's phenomenon for higher degrees. In the computer science subfields of computer-aided design and computer graphics, the term ''spline'' more frequently refers to a piecewise polynomial ( parametric) curve. Splines are popular curves in these subfields because of the simplicity of their construction, their ease and accuracy of evaluation, and their capacity to approximate complex shapes through curve fitting and interactive curve design. The term spline comes from the flexible spline devices used by shipbuilders and draftsmen to draw smooth shapes. Introduction The term "spline" is used to refer to a wide class of functions that are used in applications requiring data interpolation and/or smoothing. The dat ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Catmull–Rom Spline
In numerical analysis, a cubic Hermite spline or cubic Hermite interpolator is a spline where each piece is a third-degree polynomial specified in Hermite form, that is, by its values and first derivatives at the end points of the corresponding domain interval. Cubic Hermite splines are typically used for interpolation of numeric data specified at given argument values x_1,x_2,\ldots,x_n, to obtain a continuous function. The data should consist of the desired function value and derivative at each x_k. (If only the values are provided, the derivatives must be estimated from them.) The Hermite formula is applied to each interval (x_k, x_) separately. The resulting spline will be continuous and will have continuous first derivative. Cubic polynomial splines can be specified in other ways, the Bezier cubic being the most common. However, these two methods provide the same set of splines, and data can be easily converted between the Bézier and Hermite forms; so the names are o ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
BASIC
BASIC (Beginners' All-purpose Symbolic Instruction Code) is a family of general-purpose, high-level programming languages designed for ease of use. The original version was created by John G. Kemeny and Thomas E. Kurtz at Dartmouth College in 1963. They wanted to enable students in non-scientific fields to use computers. At the time, nearly all computers required writing custom software, which only scientists and mathematicians tended to learn. In addition to the program language, Kemeny and Kurtz developed the Dartmouth Time Sharing System (DTSS), which allowed multiple users to edit and run BASIC programs simultaneously on remote terminals. This general model became very popular on minicomputer systems like the PDP-11 and Data General Nova in the late 1960s and early 1970s. Hewlett-Packard produced an entire computer line for this method of operation, introducing the HP2000 series in the late 1960s and continuing sales into the 1980s. Many early video games trace their ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Splines (mathematics)
Spline may refer to: Mathematics * Spline (mathematics), a mathematical function used for interpolation or smoothing * Smoothing spline, a method of smoothing using a spline function Devices * Spline (mechanical), a mating feature for rotating elements * Flat spline, a device to draw curves * Spline drive, a type of screw drive * Spline cord, a type of thin rubber cord used to secure a window screen to its frame * Spline (or star filler A star filler (also known as cross filler, splines, separators and crossweb fillers) is a type of plastic insert in Cat 5 and Cat 6 cable which separates the individual stranded pair sets from each other while inside of the cable. It increases t ...), a type of plastic cable filler for CAT cable Other * Spline (alien beings), in Stephen Baxter's Xeelee Sequence novels See also * {{disambiguation ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |