|
Klein–Nishina Formula
In particle physics, the Klein–Nishina formula gives the differential cross section (i.e. the "likelihood" and angular distribution) of photons scattered from a single free electron, calculated in the lowest order of quantum electrodynamics. It was first derived in 1928 by Oskar Klein and Yoshio Nishina, constituting one of the first successful applications of the Dirac equation. The formula describes both the Thomson scattering of low energy photons (e.g. visible light) and the Compton scattering of high energy photons (e.g. x-rays and gamma-rays), showing that the total cross section and expected deflection angle decrease with increasing photon energy. Formula For an incident unpolarized photon of energy E_\gamma, the differential cross section is: : \frac = \frac r_e^2 \left(\frac\right)^ \left frac + \frac - \sin^2(\theta)\right where * r_e is the classical electron radius (~2.82 Femtometre, fm, r_e^2 is about 7.94 × 10−30 m2 or 79.4 Barn (unit), mb) * \lambda/\l ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
X-ray
An X-ray, or, much less commonly, X-radiation, is a penetrating form of high-energy electromagnetic radiation. Most X-rays have a wavelength ranging from 10 picometers to 10 nanometers, corresponding to frequencies in the range 30 petahertz to 30 exahertz ( to ) and energies in the range 145 eV to 124 keV. X-ray wavelengths are shorter than those of UV rays and typically longer than those of gamma rays. In many languages, X-radiation is referred to as Röntgen radiation, after the German scientist Wilhelm Conrad Röntgen, who discovered it on November 8, 1895. He named it ''X-radiation'' to signify an unknown type of radiation.Novelline, Robert (1997). ''Squire's Fundamentals of Radiology''. Harvard University Press. 5th edition. . Spellings of ''X-ray(s)'' in English include the variants ''x-ray(s)'', ''xray(s)'', and ''X ray(s)''. The most familiar use of X-rays is checking for fractures (broken bones), but X-rays are also used in other ways. ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
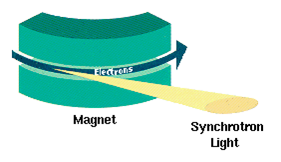
Synchrotron Radiation
Synchrotron radiation (also known as magnetobremsstrahlung radiation) is the electromagnetic radiation emitted when relativistic charged particles are subject to an acceleration perpendicular to their velocity (). It is produced artificially in some types of particle accelerators, or naturally by fast electrons moving through magnetic fields. The radiation produced in this way has a characteristic polarization and the frequencies generated can range over a large portion of the electromagnetic spectrum. Synchrotron radiation is similar to bremsstrahlung radiation, which is emitted by a charged particle when the acceleration is parallel to the direction of motion. The general term for radiation emitted by particles in a magnetic field is ''gyromagnetic radiation'', for which synchrotron radiation is the ultra-relativistic special case. Radiation emitted by charged particles moving non-relativistically in a magnetic field is called cyclotron emission. For particles in the mild ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Fine Structure Constant
In physics, the fine-structure constant, also known as the Sommerfeld constant, commonly denoted by (the Greek letter ''alpha''), is a fundamental physical constant which quantifies the strength of the electromagnetic interaction between elementary charged particles. It is a dimensionless quantity, independent of the system of units used, which is related to the strength of the coupling of an elementary charge ''e'' with the electromagnetic field, by the formula . Its numerical value is approximately , with a relative uncertainty of The constant was named by Arnold Sommerfeld, who introduced it in 1916 Equation 12a, ''"rund 7·" (about ...)'' when extending the Bohr model of the atom. quantified the gap in the fine structure of the spectral lines of the hydrogen atom, which had been measured precisely by Michelson and Morley in 1887. Definition In terms of other fundamental physical constants, may be defined as: \alpha = \frac = \frac , where * is the elementar ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Monotonic Function
In mathematics, a monotonic function (or monotone function) is a function between ordered sets that preserves or reverses the given order. This concept first arose in calculus, and was later generalized to the more abstract setting of order theory. In calculus and analysis In calculus, a function f defined on a subset of the real numbers with real values is called ''monotonic'' if and only if it is either entirely non-increasing, or entirely non-decreasing. That is, as per Fig. 1, a function that increases monotonically does not exclusively have to increase, it simply must not decrease. A function is called ''monotonically increasing'' (also ''increasing'' or ''non-decreasing'') if for all x and y such that x \leq y one has f\!\left(x\right) \leq f\!\left(y\right), so f preserves the order (see Figure 1). Likewise, a function is called ''monotonically decreasing'' (also ''decreasing'' or ''non-increasing'') if, whenever x \leq y, then f\!\left(x\right) \geq f\!\left(y\r ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Compton Wavelength
The Compton wavelength is a quantum mechanical property of a particle. The Compton wavelength of a particle is equal to the wavelength of a photon whose energy is the same as the rest energy of that particle (see mass–energy equivalence). It was introduced by Arthur Compton in 1923 in his explanation of the scattering of photons by electrons (a process known as Compton scattering). The standard Compton wavelength of a particle is given by \lambda = \frac, while its frequency is given by f = \frac, where is the Planck constant, is the particle's proper mass, and is the speed of light. The significance of this formula is shown in the derivation of the Compton shift formula. It is equivalent to the de Broglie wavelength with v = \frac . The CODATA 2018 value for the Compton wavelength of the electron is . Other particles have different Compton wavelengths. Reduced Compton wavelength The reduced Compton wavelength (barred lambda) is defined as the Compton wavelength di ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Electronvolt
In physics, an electronvolt (symbol eV, also written electron-volt and electron volt) is the measure of an amount of kinetic energy gained by a single electron accelerating from rest through an electric potential difference of one volt in vacuum. When used as a unit of energy, the numerical value of 1 eV in joules (symbol J) is equivalent to the numerical value of the charge of an electron in coulombs (symbol C). Under the 2019 redefinition of the SI base units, this sets 1 eV equal to the exact value Historically, the electronvolt was devised as a standard unit of measure through its usefulness in electrostatic particle accelerator sciences, because a particle with electric charge ''q'' gains an energy after passing through a voltage of ''V.'' Since ''q'' must be an integer multiple of the elementary charge ''e'' for any isolated particle, the gained energy in units of electronvolts conveniently equals that integer times the voltage. It is a common unit of energy with ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Four-momentum
In special relativity, four-momentum (also called momentum-energy or momenergy ) is the generalization of the classical three-dimensional momentum to four-dimensional spacetime. Momentum is a vector in three dimensions; similarly four-momentum is a four-vector in spacetime. The contravariant four-momentum of a particle with relativistic energy and three-momentum , where is the particle's three-velocity and the Lorentz factor, is p = \left(p^0 , p^1 , p^2 , p^3\right) = \left(\frac E c , p_x , p_y , p_z\right). The quantity of above is ordinary non-relativistic momentum of the particle and its rest mass. The four-momentum is useful in relativistic calculations because it is a Lorentz covariant vector. This means that it is easy to keep track of how it transforms under Lorentz transformations. The above definition applies under the coordinate convention that . Some authors use the convention , which yields a modified definition with . It is also possible to define c ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Barn (unit)
A barn (symbol: b) is a metric unit of area equal to (100 fm2). Originally used in nuclear physics for expressing the cross sectional area of nuclei and nuclear reactions, today it is also used in all fields of high-energy physics to express the cross sections of any scattering process, and is best understood as a measure of the probability of interaction between small particles. A barn is approximately the cross-sectional area of a uranium Uranium is a chemical element with the symbol U and atomic number 92. It is a silvery-grey metal in the actinide series of the periodic table. A uranium atom has 92 protons and 92 electrons, of which 6 are valence electrons. Uranium is weak ... nucleus. The barn is also the unit of area used in nuclear quadrupole resonance and nuclear magnetic resonance to quantify the interaction of a nucleus with an electric field gradient. While the barn never was an SI unit, the International Bureau of Weights and Measures, SI standards bod ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Femtometre
The magnitudes_.html" ;"title="Magnitude_(mathematics).html" ;"title="atom.html" ;"title="helium helium_atom_and_perspective_Magnitude_(mathematics)">magnitudes_">Magnitude_(mathematics).html"_;"title="atom.html"_;"title="helium_atom">helium_atom_and_perspective_Magnitude_(mathematics)">magnitudes_ The_femtometre_(American_spelling_femtometer)_symbol_fm_derived_from_the_ helium_atom_and_perspective_Magnitude_(mathematics)">magnitudes_">Magnitude_(mathematics).html"_;"title="atom.html"_;"title="helium_atom">helium_atom_and_perspective_Magnitude_(mathematics)">magnitudes_ The_femtometre_(American_spelling_femtometer)_symbol_fm_derived_from_the_Danish_language">Danish_and_ helium_atom_and_perspective_Magnitude_(mathematics)">magnitudes_">Magnitude_(mathematics).html"_;"title="atom.html"_;"title="helium_atom">helium_atom_and_perspective_Magnitude_(mathematics)">magnitudes_ The_femtometre_(American_spelling_femtometer)_symbol_fm_derived_from_the_Danish_language">Danish_and_Norwegian_ ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Classical Electron Radius
The classical electron radius is a combination of fundamental physical quantities that define a length scale for problems involving an electron interacting with electromagnetic radiation. It links the classical electrostatic self-interaction energy of a homogeneous charge distribution to the electron's relativistic mass–energy. According to modern understanding, the electron is a point particle with a point charge and no spatial extent. Nevertheless, it is useful to define a length that characterizes electron interactions in atomic-scale problems. The classical electron radius is given as :r_\text = \frac\frac = 2.817 940 3227(19) \times 10^ \text = 2.817 940 3227(19) \text , where e is the elementary charge, m_ is the electron mass, c is the speed of light, and \varepsilon_0 is the permittivity of free space. This numerical value is several times larger than the radius of the proton. In cgs units, the permittivity factor and \frac do not enter, but the classical electron ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Gamma-ray
A gamma ray, also known as gamma radiation (symbol γ or \gamma), is a penetrating form of electromagnetic radiation arising from the radioactive decay of atomic nuclei. It consists of the shortest wavelength electromagnetic waves, typically shorter than those of X-rays. With frequencies above 30 exahertz (), it imparts the highest photon energy. Paul Villard, a French chemist and physicist, discovered gamma radiation in 1900 while studying radiation emitted by radium. In 1903, Ernest Rutherford named this radiation ''gamma rays'' based on their relatively strong penetration of matter; in 1900 he had already named two less penetrating types of decay radiation (discovered by Henri Becquerel) alpha rays and beta rays in ascending order of penetrating power. Gamma rays from radioactive decay are in the energy range from a few kiloelectronvolts ( keV) to approximately 8 megaelectronvolts ( MeV), corresponding to the typical energy levels in nuclei with reasonably long lifet ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |