|
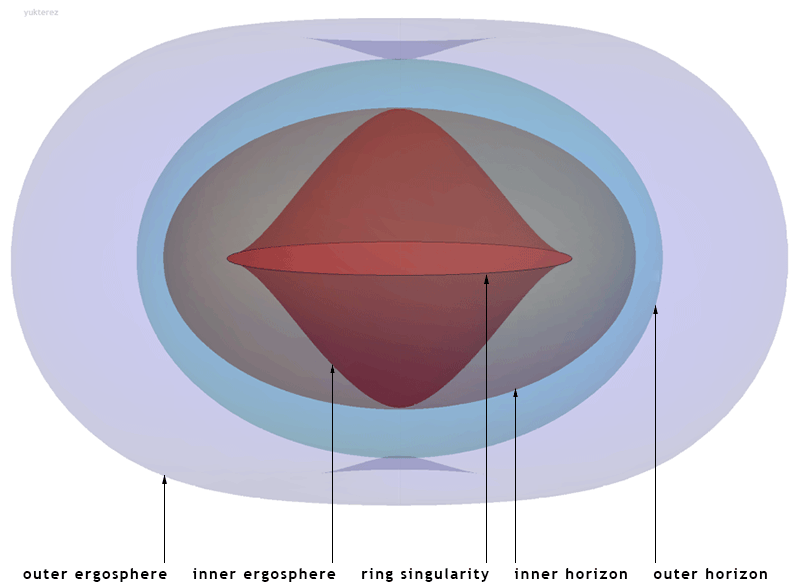
Kerr Spacetime
The Kerr metric or Kerr geometry describes the geometry of empty spacetime around a rotating uncharged axially symmetric black hole with a quasispherical event horizon. The Kerr metric is an exact solution of the Einstein field equations of general relativity; these equations are highly non-linear, which makes exact solutions very difficult to find. Overview The Kerr metric is a generalization to a rotating body of the Schwarzschild metric, discovered by Karl Schwarzschild in 1915, which described the geometry of spacetime around an uncharged, spherically symmetric, and non-rotating body. The corresponding solution for a ''charged'', spherical, non-rotating body, the Reissner–Nordström metric, was discovered soon afterwards (1916–1918). However, the exact solution for an uncharged, ''rotating'' black hole, the Kerr metric, remained unsolved until 1963, when it was discovered by Roy Kerr.Melia, Fulvio (2009). "Cracking the Einstein code: relativity and the birth of black h ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Spacetime
In physics, spacetime is a mathematical model that combines the three dimensions of space and one dimension of time into a single four-dimensional manifold. Spacetime diagrams can be used to visualize relativistic effects, such as why different observers perceive differently where and when events occur. Until the 20th century, it was assumed that the three-dimensional geometry of the universe (its spatial expression in terms of coordinates, distances, and directions) was independent of one-dimensional time. The physicist Albert Einstein helped develop the idea of spacetime as part of his theory of relativity. Prior to his pioneering work, scientists had two separate theories to explain physical phenomena: Isaac Newton's laws of physics described the motion of massive objects, while James Clerk Maxwell's electromagnetic models explained the properties of light. However, in 1905, Einstein based a work on special relativity on two postulates: * The laws of physics are invariant ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Lense–Thirring Precession
In general relativity, Lense–Thirring precession or the Lense–Thirring effect (; named after Josef Lense and Hans Thirring) is a Theory of relativity, relativistic correction to the precession of a gyroscope near a large rotating mass such as the Earth. It is a gravitomagnetism, gravitomagnetic frame-dragging effect. It is a prediction of general relativity consisting of secular variation, secular precessions of the longitude of the ascending node and the argument of pericenter of a test particle freely orbiting a central spinning mass endowed with angular momentum S. The difference between de Sitter precession and the Lense–Thirring effect is that the de Sitter effect is due simply to the presence of a central mass, whereas the Lense–Thirring effect is due to the rotation of the central mass. The total precession is calculated by combining the de Sitter precession with the Lense–Thirring precession. According to a 2007 historical analysis by Herbert Pfister, the effect ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Ernst Equation
In mathematics, the Ernst equation is an integrable non-linear partial differential equation, named after the American physicist . The Ernst equation The equation reads: \Re(u)(u_+u_r/r+u_) = (u_r)^2+(u_z)^2. For its Lax pair and other features see e.g. and references therein. Usage The ''Ernst equation'' is employed in order to produce the exact solutions of the Einstein's equations in the general theory of relativity General relativity, also known as the general theory of relativity and Einstein's theory of gravity, is the differential geometry, geometric scientific theory, theory of gravitation published by Albert Einstein in 1915 and is the current descr .... References Partial differential equations General relativity Integrable systems {{theoretical-physics-stub ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Newman–Penrose Formalism
The Newman–Penrose (NP) formalism The original paper by Newman and Penrose, which introduces the formalism, and uses it to derive example results.Ezra T Newman, Roger Penrose. ''Errata: An Approach to Gravitational Radiation by a Method of Spin Coefficients''. Journal of Mathematical Physics, 1963, 4(7): 998. is a set of notation developed by Ezra T. Newman and Roger Penrose for general relativity (GR). Their notation is an effort to treat general relativity in terms of spinor notation, which introduces complex forms of the usual variables used in GR. The NP formalism is itself a special case of the tetrad formalism, where the tensors of the theory are projected onto a complete vector basis at each point in spacetime. Usually this vector basis is chosen to reflect some symmetry of the spacetime, leading to simplified expressions for physical observables. In the case of the NP formalism, the vector basis chosen is a null tetrad: a set of four null vectors—two real, and a com ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Newman–Janis Algorithm
In general relativity, the Newman–Janis algorithm (NJA) is a complexification technique for finding exact solutions to the Einstein field equations. In 1964, Newman and Janis showed that the Kerr metric could be obtained from the Schwarzschild metric by means of a coordinate transformation and allowing the radial coordinate to take on complex values. Originally, no clear reason for why the algorithm works was known. In 1998, Drake and Szekeres gave a detailed explanation of the success of the algorithm and proved the uniqueness of certain solutions. In particular, the only perfect fluid solution generated by NJA is the Kerr metric and the only Petrov type D solution is the Kerr–Newman metric. The algorithm works well on ''ƒ''(''R'') and Einstein–Maxwell–Dilaton theories, but doesn't return expected results on Braneworld and Born–Infield theories. See also * Birkhoff's theorem (relativity) In general relativity, Birkhoff's theorem states that any spherically s ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
First Observation Of Gravitational Waves
The first direct observation of gravitational waves was made on 14 September 2015 and was announced by the LIGO and Virgo collaborations on 11 February 2016. Previously, gravitational waves had been inferred only indirectly, via their effect on the timing of pulsars in binary star systems. The waveform, detected by both LIGO observatories, matched the predictions of general relativity for a gravitational wave emanating from the inward spiral and merger of a pair of black holes of around 36 and 29 solar masses and the subsequent "ringdown" of the single resulting black hole. The signal was named GW150914 (from ''gravitational wave'' and the date of observation 2015-09-14). It was also the first observation of a binary black hole merger, demonstrating both the existence of binary stellar-mass black hole systems and the fact that such mergers could occur within the current age of the universe. This first direct observation was reported around the world as a remarkable accompl ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Invariant Mass
The invariant mass, rest mass, intrinsic mass, proper mass, or in the case of bound systems simply mass, is the portion of the total mass of an object or system of objects that is independent of the overall motion of the system. More precisely, it is a characteristic of the system's total energy and momentum that is the same in all frames of reference related by Lorentz transformations.Lawrence S. LernerPhysics for Scientists and Engineers, Volume 2, page 1073 1997. If a center-of-momentum frame exists for the system, then the invariant mass of a system is equal to its total mass in that "rest frame". In other reference frames, where the system's momentum is nonzero, the total mass (a.k.a. relativistic mass) of the system is greater than the invariant mass, but the invariant mass remains unchanged. Because of mass–energy equivalence, the rest energy of the system is simply the invariant mass times the speed of light squared. Similarly, the total energy of the system is its tot ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Coordinate System
In geometry, a coordinate system is a system that uses one or more numbers, or coordinates, to uniquely determine the position of the points or other geometric elements on a manifold such as Euclidean space. The order of the coordinates is significant, and they are sometimes identified by their position in an ordered tuple and sometimes by a letter, as in "the ''x''-coordinate". The coordinates are taken to be real numbers in elementary mathematics, but may be complex numbers or elements of a more abstract system such as a commutative ring. The use of a coordinate system allows problems in geometry to be translated into problems about numbers and ''vice versa''; this is the basis of analytic geometry. Common coordinate systems Number line The simplest example of a coordinate system is the identification of points on a line with real numbers using the ''number line''. In this system, an arbitrary point ''O'' (the ''origin'') is chosen on a given line. The coordinate of a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mass
Mass is an intrinsic property of a body. It was traditionally believed to be related to the quantity of matter in a physical body, until the discovery of the atom and particle physics. It was found that different atoms and different elementary particles, theoretically with the same amount of matter, have nonetheless different masses. Mass in modern physics has multiple definitions which are conceptually distinct, but physically equivalent. Mass can be experimentally defined as a measure of the body's inertia, meaning the resistance to acceleration (change of velocity) when a net force is applied. The object's mass also determines the strength of its gravitational attraction to other bodies. The SI base unit of mass is the kilogram (kg). In physics, mass is not the same as weight, even though mass is often determined by measuring the object's weight using a spring scale, rather than balance scale comparing it directly with known masses. An object on the Moon would weigh le ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Coordinate Singularity
A coordinate singularity occurs when an apparent singularity or discontinuity occurs in one coordinate frame that can be removed by choosing a different frame. An example is the apparent (longitudinal) singularity at the 90 degree latitude in spherical coordinates. An object moving due north (for example, along the line 0 degrees longitude) on the surface of a sphere will suddenly experience an instantaneous change in longitude at the pole (i.e., jumping from longitude 0 to longitude 180 degrees). In fact, longitude is not uniquely defined at the poles. This discontinuity, however, is only apparent; it is an artifact of the coordinate system chosen, which is singular at the poles. A different coordinate system would eliminate the apparent discontinuity, e.g. by replacing the latitude/longitude representation with an -vector representation. Stephen Hawking aptly summed this up, when once asking the question, "What lies north of the North Pole?". [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Cosmic Dawn Center
The Niels Bohr Institute (Danish: ''Niels Bohr Institutet'') is a research institute of the University of Copenhagen. The research of the institute spans astronomy, geophysics, nanotechnology, particle physics, quantum mechanics and biophysics. Overview The institute was founded in 1921, as the Institute for Theoretical Physics of the University of Copenhagen, by the Danish theoretical physicist Niels Bohr, who had been on the staff of the University of Copenhagen since 1914, and who had been lobbying for its creation since his appointment as professor in 1916. On the 80th anniversary of Niels Bohr's birth – October 7, 1965 – the Institute officially became the Niels Bohr Institute. Much of its original funding came from the charitable foundation of the Carlsberg brewery, and later from the Rockefeller Foundation. During the 1920s, and 1930s, the institute was the center of the developing disciplines of atomic physics and quantum physics. Physicists from across Europe (and ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
E (mathematical Constant)
The number , also known as Euler's number, is a mathematical constant approximately equal to 2.71828 that can be characterized in many ways. It is the base of the natural logarithms. It is the limit of as approaches infinity, an expression that arises in the study of compound interest. It can also be calculated as the sum of the infinite series e = \sum\limits_^ \frac = 1 + \frac + \frac + \frac + \cdots. It is also the unique positive number such that the graph of the function has a slope of 1 at . The (natural) exponential function is the unique function that equals its own derivative and satisfies the equation ; hence one can also define as . The natural logarithm, or logarithm to base , is the inverse function to the natural exponential function. The natural logarithm of a number can be defined directly as the area under the curve between and , in which case is the value of for which this area equals one (see image). There are various other characteriz ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |