|
Korkine–Zolotarev Lattice Basis Reduction Algorithm
The Korkine–Zolotarev (KZ) lattice basis reduction algorithm or Hermite–Korkine–Zolotarev (HKZ) algorithm is a lattice reduction algorithm. For lattices in \mathbb^n it yields a lattice basis with orthogonality defect at most n^n, unlike the 2^ bound of the LLL reduction. KZ has exponential complexity versus the polynomial complexity of the LLL reduction algorithm, however it may still be preferred for solving multiple closest vector problems (CVPs) in the same lattice, where it can be more efficient. History The definition of a KZ-reduced basis was given by Aleksandr Korkin and Yegor Ivanovich Zolotarev in 1877, a strengthened version of Hermite reduction. The first algorithm for constructing a KZ-reduced basis was given in 1983 by Kannan. The block Korkine-Zolotarev (BKZ) algorithm was introduced in 1987. Definition A KZ-reduced basis for a lattice is defined as follows:Micciancio & Goldwasser, p.133, definition 7.8 Given a basis :\mathbf=\, define its Gram� ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Lattice Reduction
In mathematics, the goal of lattice basis reduction is to find a basis with short, nearly orthogonal vectors when given an integer lattice basis as input. This is realized using different algorithms, whose running time is usually at least exponential in the dimension of the lattice. Nearly orthogonal One measure of ''nearly orthogonal'' is the orthogonality defect. This compares the product of the lengths of the basis vectors with the volume of the parallelepiped they define. For perfectly orthogonal basis vectors, these quantities would be the same. Any particular basis of n vectors may be represented by a matrix B, whose columns are the basis vectors b_i, i = 1, \ldots, n. In the fully dimensional case where the number of basis vectors is equal to the dimension of the space they occupy, this matrix is square, and the volume of the fundamental parallelepiped is simply the absolute value of the determinant of this matrix \det(B). If the number of vectors is less than the dimens ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Algorithm
In mathematics and computer science, an algorithm () is a finite sequence of Rigour#Mathematics, mathematically rigorous instructions, typically used to solve a class of specific Computational problem, problems or to perform a computation. Algorithms are used as specifications for performing calculations and data processing. More advanced algorithms can use Conditional (computer programming), conditionals to divert the code execution through various routes (referred to as automated decision-making) and deduce valid inferences (referred to as automated reasoning). In contrast, a Heuristic (computer science), heuristic is an approach to solving problems without well-defined correct or optimal results.David A. Grossman, Ophir Frieder, ''Information Retrieval: Algorithms and Heuristics'', 2nd edition, 2004, For example, although social media recommender systems are commonly called "algorithms", they actually rely on heuristics as there is no truly "correct" recommendation. As an e ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Lenstra–Lenstra–Lovász Lattice Basis Reduction Algorithm
The Lenstra–Lenstra–Lovász (LLL) lattice basis reduction algorithm is a polynomial time lattice reduction algorithm invented by Arjen Lenstra, Hendrik Lenstra and László Lovász in 1982. Given a basis \mathbf = \ with ''n''-dimensional integer coordinates, for a lattice L (a discrete subgroup of R''n'') with d \leq n , the LLL algorithm calculates an ''LLL-reduced'' (short, nearly orthogonal) lattice basis in time \mathcal O(d^5n\log^3 B) where B is the largest length of \mathbf_i under the Euclidean norm, that is, B = \max\left(\, \mathbf_1\, _2, \, \mathbf_2\, _2, \dots, \, \mathbf_d\, _2\right). The original applications were to give polynomial-time algorithms for factorizing polynomials with rational coefficients, for finding simultaneous rational approximations to real numbers, and for solving the integer linear programming problem in fixed dimensions. LLL reduction The precise definition of LLL-reduced is as follows: Given a basis \mathbf=\, define its Gram– ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Closest Vector Problem
In computer science, lattice problems are a class of optimization problems related to mathematical objects called '' lattices''. The conjectured intractability of such problems is central to the construction of secure lattice-based cryptosystems: lattice problems are an example of NP-hard problems which have been shown to be average-case hard, providing a test case for the security of cryptographic algorithms. In addition, some lattice problems which are worst-case hard can be used as a basis for extremely secure cryptographic schemes. The use of worst-case hardness in such schemes makes them among the very few schemes that are very likely secure even against quantum computers. For applications in such cryptosystems, lattices over vector spaces (often \mathbb^n) or free modules (often \mathbb^n) are generally considered. For all the problems below, assume that we are given (in addition to other more specific inputs) a basis for the vector space ''V'' and a norm ''N''. The norm ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Aleksandr Korkin
Aleksandr Nikolayevich Korkin (; – ) was a Russian mathematician. He made contribution to the development of partial differential equations, and was second only to Chebyshev among the founders of the Saint Petersburg Mathematical School. Among others, his students included Yegor Ivanovich Zolotarev Yegor (Egor) Ivanovich Zolotaryov () (31 March 1847, Saint Petersburg – 19 July 1878, Saint Petersburg) was a Russian mathematician. Biography Yegor was born as a son of Agafya Izotovna Zolotaryova and the merchant Ivan Vasilevich Zolotary .... Some publications * * * References External links * *Korkin's Biography, the St. Petersburg University Pages (in Russian, but with an image) 1837 births 1908 deaths People from Vologda Oblast People from Vologda Governorate 19th-century mathematicians from the Russian Empire Mathematical analysts {{Russia-mathematician-stub ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Yegor Ivanovich Zolotarev
Yegor (Egor) Ivanovich Zolotaryov () (31 March 1847, Saint Petersburg – 19 July 1878, Saint Petersburg) was a Russian mathematician. Biography Yegor was born as a son of Agafya Izotovna Zolotaryova and the merchant Ivan Vasilevich Zolotaryov in Saint Petersburg, Imperial Russia. In 1857 he began to study at the fifth St Petersburg gymnasium, a school which centred on mathematics and natural science. He finished it with the silver medal in 1863. In the same year he was allowed to be an auditor at the physico-mathematical faculty of St Petersburg university. He had not been able to become a student before 1864 because he was too young. Among his academic teachers were Somov, Chebyshev and Aleksandr Korkin, with whom he would have a tight scientific friendship. In November 1867 he defended his Kandidat thesis ''“About the Integration of Gyroscope Equations”'', after 10 months there followed his thesis pro venia legendi ''About one question on Minima''. With this wor ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Hermite Normal Form
In linear algebra, the Hermite normal form is an analogue of reduced echelon form for matrices over the integers \Z. Just as reduced echelon form can be used to solve problems about the solution to the linear system Ax=b where x \in \mathbb^n, the Hermite normal form can solve problems about the solution to the linear system Ax=b where this time x is restricted to have integer coordinates only. Other applications of the Hermite normal form include integer programming, cryptography, and abstract algebra. Definition Various authors may prefer to talk about Hermite normal form in either row-style or column-style. They are essentially the same up to transposition. Row-style Hermite normal form A matrix A \in \mathbb^ has a (row) Hermite normal form H if there is a square unimodular matrix U where H=UA. H has the following restrictions: # H is upper triangular (that is, h_=0 for i>j), and any rows of zeros are located below any other row. # The leading coefficient (the first nonzero e ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Basis (linear Algebra)
In mathematics, a Set (mathematics), set of elements of a vector space is called a basis (: bases) if every element of can be written in a unique way as a finite linear combination of elements of . The coefficients of this linear combination are referred to as components or coordinates of the vector with respect to . The elements of a basis are called . Equivalently, a set is a basis if its elements are linearly independent and every element of is a linear combination of elements of . In other words, a basis is a linearly independent spanning set. A vector space can have several bases; however all the bases have the same number of elements, called the dimension (vector space), dimension of the vector space. This article deals mainly with finite-dimensional vector spaces. However, many of the principles are also valid for infinite-dimensional vector spaces. Basis vectors find applications in the study of crystal structures and frame of reference, frames of reference. De ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
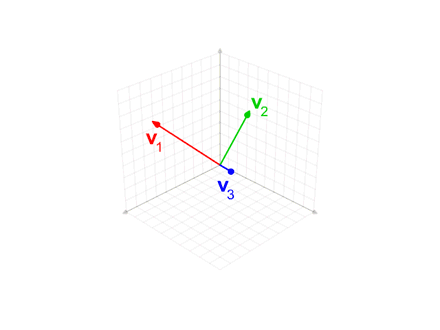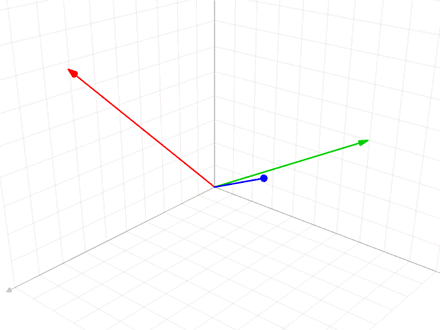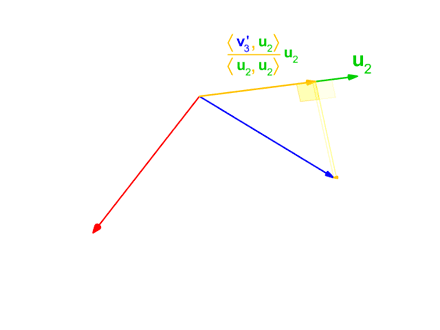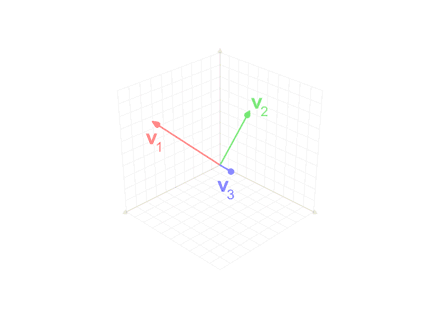
Gram–Schmidt Process
In mathematics, particularly linear algebra and numerical analysis, the Gram–Schmidt process or Gram-Schmidt algorithm is a way of finding a set of two or more vectors that are perpendicular to each other. By technical definition, it is a method of constructing an orthonormal basis from a set of vector (geometry), vectors in an inner product space, most commonly the Euclidean space \mathbb^n equipped with the standard inner product. The Gram–Schmidt process takes a finite set, finite, linearly independent set of vectors S = \ for and generates an orthogonal set S' = \ that spans the same k-dimensional subspace of \mathbb^n as S. The method is named after Jørgen Pedersen Gram and Erhard Schmidt, but Pierre-Simon Laplace had been familiar with it before Gram and Schmidt. In the theory of Lie group decompositions, it is generalized by the Iwasawa decomposition. The application of the Gram–Schmidt process to the column vectors of a full column rank (linear algebra), rank mat ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Theory Of Cryptography
A theory is a systematic and rational form of abstract thinking about a phenomenon, or the conclusions derived from such thinking. It involves contemplative and logical reasoning, often supported by processes such as observation, experimentation, and research. Theories can be scientific, falling within the realm of empirical and testable knowledge, or they may belong to non-scientific disciplines, such as philosophy, art, or sociology. In some cases, theories may exist independently of any formal discipline. In modern science, the term "theory" refers to Scientific theory, scientific theories, a well-confirmed type of explanation of nature, made in a way Consistency, consistent with the scientific method, and fulfilling the Scientific theory#Characteristics of theories, criteria required by modern science. Such theories are described in such a way that scientific tests should be able to provide Empirical evidence, empirical support for it, or Empirical evidence, empirical contradi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Computational Number Theory
In mathematics and computer science, computational number theory, also known as algorithmic number theory, is the study of computational methods for investigating and solving problems in number theory and arithmetic geometry, including algorithms for primality testing and integer factorization, finding solutions to diophantine equations, and explicit methods in arithmetic geometry. Computational number theory has applications to cryptography, including RSA, elliptic curve cryptography and post-quantum cryptography, and is used to investigate conjectures and open problems in number theory, including the Riemann hypothesis, the Birch and Swinnerton-Dyer conjecture, the ABC conjecture, the modularity conjecture, the Sato-Tate conjecture, and explicit aspects of the Langlands program. Software packages * Magma computer algebra system * SageMath * Number Theory Library * PARI/GP * Fast Library for Number Theory Further reading * Michael E. Pohst (1993): ''Computational ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |