|
Kneser's Theorem (combinatorics)
In the branch of mathematics known as additive combinatorics, Kneser's theorem can refer to one of several related theorems regarding the sizes of certain sumsets in abelian groups. These are named after Martin Kneser, who published them in 1953 and 1956. They may be regarded as extensions of the Cauchy–Davenport theorem, which also concerns sumsets in groups but is restricted to groups whose order is a prime number. The first three statements deal with sumsets whose size (in various senses) is strictly smaller than the sum of the size of the summands. The last statement deals with the case of equality for Haar measure in connected compact abelian groups. Strict inequality If G is an abelian group and C is a subset of G , the group H(C):= \ is the ''stabilizer'' of C . Cardinality Let G be an abelian group. If A and B are nonempty finite subsets of G satisfying , A + B, < , A, + , B, and is the stabilizer of [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Additive Combinatorics
Additive combinatorics is an area of combinatorics in mathematics. One major area of study in additive combinatorics are ''inverse problems'': given the size of the sumset is small, what can we say about the structures of and ? In the case of the integers, the classical Freiman's theorem provides a partial answer to this question in terms of multi-dimensional arithmetic progressions. Another typical problem is to find a lower bound for in terms of and . This can be viewed as an inverse problem with the given information that is sufficiently small and the structural conclusion is then of the form that either or is the empty set; however, in literature, such problems are sometimes considered to be direct problems as well. Examples of this type include the Erdős–Heilbronn Conjecture (for a restricted sumset) and the Cauchy–Davenport Theorem. The methods used for tackling such questions often come from many different fields of mathematics, including combinatorics, ergod ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Schnirelmann Density
In additive number theory, the Schnirelmann density of a sequence of numbers is a way to measure how "dense" the sequence is. It is named after Russian mathematician Lev Schnirelmann, who was the first to study it.Schnirelmann, L.G. (1930).On the additive properties of numbers, first published in "Proceedings of the Don Polytechnic Institute in Novocherkassk" (in Russian), vol XIV (1930), pp. 3-27, and reprinted in "Uspekhi Matematicheskikh Nauk" (in Russian), 1939, no. 6, 9–25.Schnirelmann, L.G. (1933). First published asÜber additive Eigenschaften von Zahlen in "Mathematische Annalen" (in German), vol 107 (1933), 649-690, and reprinted asOn the additive properties of numbers in "Uspekhin. Matematicheskikh Nauk" (in Russian), 1940, no. 7, 7–46. Definition The Schnirelmann density of a set of natural numbers ''A'' is defined as :\sigma A = \inf_ \frac, where ''A''(''n'') denotes the number of elements of ''A'' not exceeding ''n'' and inf is infimum.Nathanson (1996) pp.191–19 ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
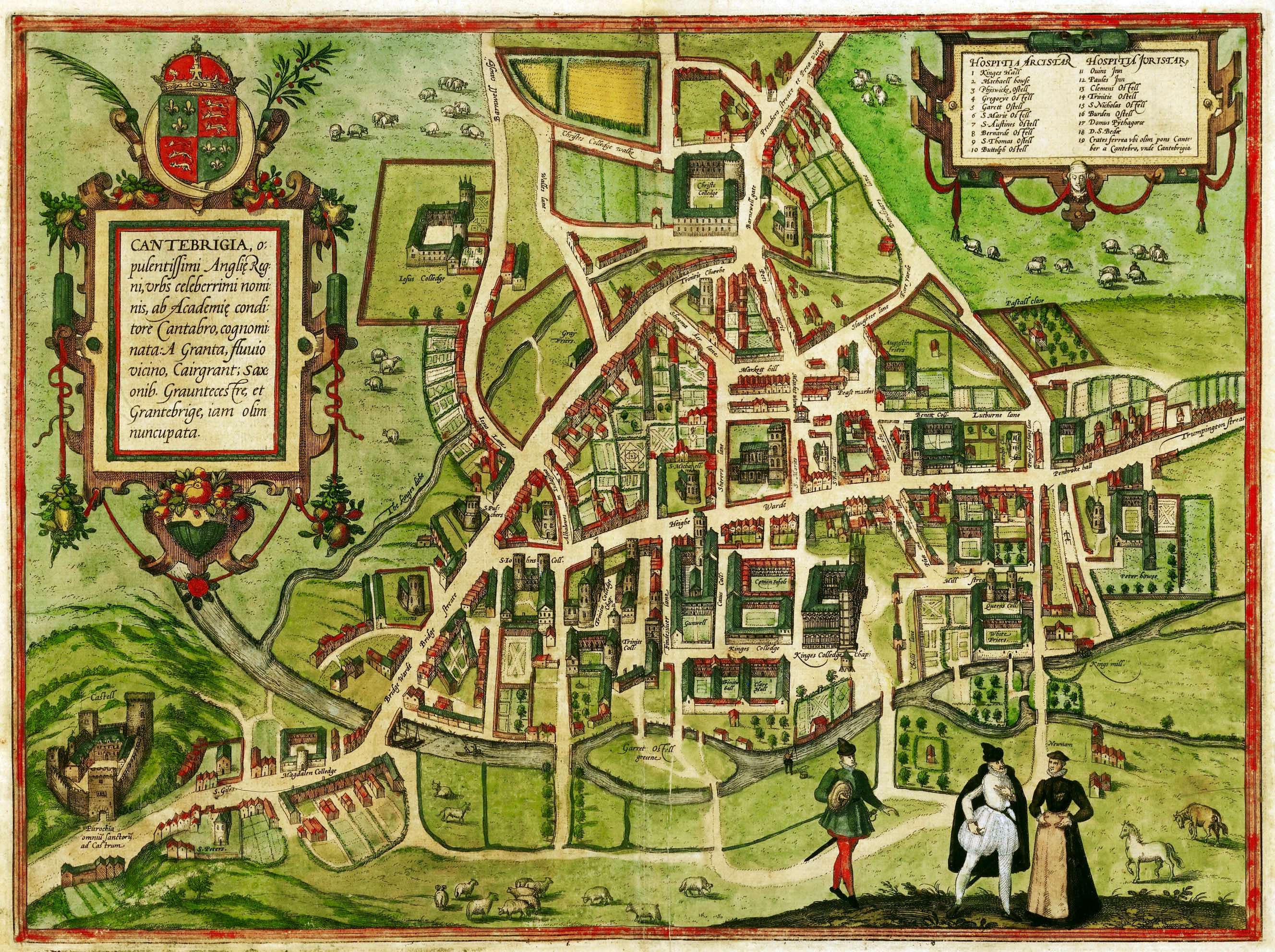
Cambridge
Cambridge ( ) is a List of cities in the United Kingdom, city and non-metropolitan district in the county of Cambridgeshire, England. It is the county town of Cambridgeshire and is located on the River Cam, north of London. As of the 2021 United Kingdom census, the population of the City of Cambridge was 145,700; the population of the wider built-up area (which extends outside the city council area) was 181,137. (2021 census) There is archaeological evidence of settlement in the area as early as the Bronze Age, and Cambridge became an important trading centre during the Roman Britain, Roman and Viking eras. The first Town charter#Municipal charters, town charters were granted in the 12th century, although modern city status was not officially conferred until 1951. The city is well known as the home of the University of Cambridge, which was founded in 1209 and consistently ranks among the best universities in the world. The buildings of the university include King's College Chap ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Cambridge University Press
Cambridge University Press was the university press of the University of Cambridge. Granted a letters patent by King Henry VIII in 1534, it was the oldest university press in the world. Cambridge University Press merged with Cambridge Assessment to form Cambridge University Press and Assessment under Queen Elizabeth II's approval in August 2021. With a global sales presence, publishing hubs, and offices in more than 40 countries, it published over 50,000 titles by authors from over 100 countries. Its publications include more than 420 academic journals, monographs, reference works, school and university textbooks, and English language teaching and learning publications. It also published Bibles, runs a bookshop in Cambridge, sells through Amazon, and has a conference venues business in Cambridge at the Pitt Building and the Sir Geoffrey Cass Sports and Social Centre. It also served as the King's Printer. Cambridge University Press, as part of the University of Cambridge, was a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Springer Science+Business Media
Springer Science+Business Media, commonly known as Springer, is a German multinational publishing company of books, e-books and peer-reviewed journals in science, humanities, technical and medical (STM) publishing. Originally founded in 1842 in Berlin, it expanded internationally in the 1960s, and through mergers in the 1990s and a sale to venture capitalists it fused with Wolters Kluwer and eventually became part of Springer Nature in 2015. Springer has major offices in Berlin, Heidelberg, Dordrecht, and New York City. History Julius Springer founded Springer-Verlag in Berlin in 1842 and his son Ferdinand Springer grew it from a small firm of 4 employees into Germany's then second-largest academic publisher with 65 staff in 1872.Chronology ". Springer Science+Business Media. In 1964, Springer expanded its business internationally, op ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |