|
Kilodegree Extremely Little Telescope
The Kilodegree Extremely Little Telescope (or KELT) is an astronomical observation system formed by two robotic telescopes that are conducting a survey for transiting exoplanets around bright stars. The project is jointly administered by members of Ohio State University Department of Astronomy, the Vanderbilt University Department of Physics and Astronomy Astronomy Group, the Lehigh University Department of Physics, and the South African Astronomical Observatory (SAAO). KELT Telescopes KELT consists of two telescopes, KELT-North in Arizona in the United States, and KELT-South at the SAAO observing station near Sutherland, South Africa. Each KELT telescope consists of a wide field (26 degrees by 26 degrees) medium format telephoto lens with a 4.2 cm aperture, mounted in front of a 4k x 4k Apogee CCD. Each can also be equipped with an alternative narrower field (10.8 degrees by 10.8 degrees) lens with a 7.1 cm aperture for a narrow angle campaign mode. KELT-North u ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Robotic Telescope
A robotic telescope is an astronomical telescope and detector system that makes observations without the intervention of a human. In astronomical disciplines, a telescope qualifies as robotic if it makes those observations without being operated by a human, even if a human has to initiate the observations at the beginning of the night or end them in the morning. It may have software agents using artificial intelligence that assist in various ways such as automatic scheduling. A robotic telescope is distinct from a remote telescope, though an instrument can be both robotic and remote. By 2004, robotic observations accounted for an overwhelming percentage of the published scientific information on asteroid orbits and discoveries, variable star studies, supernova light curves and discoveries, comet orbits and gravitational microlensing observations. All early phase gamma ray burst observations were carried by robotic telescopes. Design Robotic telescopes are complex systems that ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
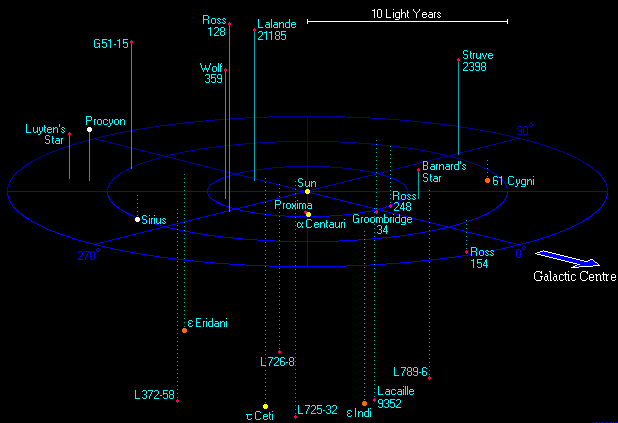
Light Year
A light-year, alternatively spelled light year, is a large unit of length used to express astronomical distances and is equivalent to about 9.46 trillion kilometers (), or 5.88 trillion miles ().One trillion here is taken to be 1012 (one million million, or billion in long scale). As defined by the International Astronomical Union (IAU), a light-year is the distance that light travels in a vacuum in one Julian year (365.25 days). Because it includes the time-measurement word "year", the term ''light-year'' is sometimes misinterpreted as a unit of time. The ''light-year'' is most often used when expressing distances to stars and other distances on a galactic scale, especially in non-specialist contexts and popular science publications. The unit most commonly used in professional astronomy is the parsec (symbol: pc, about 3.26 light-years) which derives from astrometry; it is the distance at which one astronomical unit subtends an angle of one second of arc. Defini ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Degree (angle)
A degree (in full, a degree of arc, arc degree, or arcdegree), usually denoted by ° (the degree symbol), is a measurement of a plane (mathematics), plane angle in which one Turn (geometry), full rotation is 360 degrees. It is not an SI unit—the SI unit of angular measure is the radian—but it is mentioned in the SI Brochure, SI brochure as an Non-SI units mentioned in the SI, accepted unit. Because a full rotation equals 2 radians, one degree is equivalent to radians. History The original motivation for choosing the degree as a unit of rotations and angles is unknown. One theory states that it is related to the fact that 360 is approximately the number of days in a year. Ancient astronomers noticed that the sun, which follows through the ecliptic path over the course of the year, seems to advance in its path by approximately one degree each day. Some ancient calendars, such as the Iranian calendar, Persian calendar and the Babylonian calendar, used 360 days for a year. ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Inclination
Orbital inclination measures the tilt of an object's orbit around a celestial body. It is expressed as the angle between a Plane of reference, reference plane and the orbital plane or Axis of rotation, axis of direction of the orbiting object. For a satellite orbiting the Earth directly above the Equator, the plane of the satellite's orbit is the same as the Earth's equatorial plane, and the satellite's orbital inclination is 0°. The general case for a circular orbit is that it is tilted, spending half an orbit over the northern hemisphere and half over the southern. If the orbit swung between 20° north latitude and 20° south latitude, then its orbital inclination would be 20°. Orbits The inclination is one of the six orbital elements describing the shape and orientation of a celestial orbit. It is the angle between the orbital plane and the plane of reference, normally stated in degree (angle), degrees. For a satellite orbiting a planet, the plane of reference is usually ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Eccentricity (orbit)
In astrodynamics, the orbital eccentricity of an astronomical object is a dimensionless parameter that determines the amount by which its orbit around another body deviates from a perfect circle. A value of 0 is a circular orbit, values between 0 and 1 form an elliptic orbit, 1 is a parabolic escape orbit (or capture orbit), and greater than 1 is a hyperbola. The term derives its name from the parameters of conic sections, as every Kepler orbit is a conic section. It is normally used for the isolated two-body problem, but extensions exist for objects following a rosette orbit through the Galaxy. Definition In a two-body problem with inverse-square-law force, every orbit is a Kepler orbit. The eccentricity of this Kepler orbit is a non-negative number that defines its shape. The eccentricity may take the following values: * circular orbit: ''e'' = 0 * elliptic orbit: 0 < ''e'' < 1 * [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Astronomical Unit
The astronomical unit (symbol: au, or or AU) is a unit of length, roughly the distance from Earth to the Sun and approximately equal to or 8.3 light-minutes. The actual distance from Earth to the Sun varies by about 3% as Earth orbits the Sun, from a maximum (aphelion) to a minimum (perihelion) and back again once each year. The astronomical unit was originally conceived as the average of Earth's aphelion and perihelion; however, since 2012 it has been defined as exactly (see below for several conversions). The astronomical unit is used primarily for measuring distances within the Solar System or around other stars. It is also a fundamental component in the definition of another unit of astronomical length, the parsec. History of symbol usage A variety of unit symbols and abbreviations have been in use for the astronomical unit. In a 1976 resolution, the International Astronomical Union (IAU) had used the symbol ''A'' to denote a length equal to the astronomical ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Semimajor Axis
In geometry, the major axis of an ellipse is its longest diameter: a line segment that runs through the center and both foci, with ends at the two most widely separated points of the perimeter. The semi-major axis (major semiaxis) is the longest semidiameter or one half of the major axis, and thus runs from the centre, through a focus, and to the perimeter. The semi-minor axis (minor semiaxis) of an ellipse or hyperbola is a line segment that is at right angles with the semi-major axis and has one end at the center of the conic section. For the special case of a circle, the lengths of the semi-axes are both equal to the radius of the circle. The length of the semi-major axis of an ellipse is related to the semi-minor axis's length through the eccentricity and the semi-latus rectum \ell, as follows: The semi-major axis of a hyperbola is, depending on the convention, plus or minus one half of the distance between the two branches. Thus it is the distance from the center t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Orbital Period
The orbital period (also revolution period) is the amount of time a given astronomical object takes to complete one orbit around another object. In astronomy, it usually applies to planets or asteroids orbiting the Sun, moons orbiting planets, exoplanets orbiting other stars, or binary stars. For celestial objects in general, the sidereal period ( sidereal year) is referred to by the orbital period, determined by a 360° revolution of one body around its primary, e.g. Earth around the Sun, relative to the fixed stars projected in the sky. Orbital periods can be defined in several ways. The tropical period is more particularly about the position of the parent star. It is the basis for the solar year, and respectively the calendar year. The synodic period incorporates not only the orbital relation to the parent star, but also to other celestial objects, making it not a mere different approach to the orbit of an object around its parent, but a period of orbital relations ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Density
Density (volumetric mass density or specific mass) is the substance's mass per unit of volume. The symbol most often used for density is ''ρ'' (the lower case Greek letter rho), although the Latin letter ''D'' can also be used. Mathematically, density is defined as mass divided by volume: : \rho = \frac where ''ρ'' is the density, ''m'' is the mass, and ''V'' is the volume. In some cases (for instance, in the United States oil and gas industry), density is loosely defined as its weight per unit volume, although this is scientifically inaccurate – this quantity is more specifically called specific weight. For a pure substance the density has the same numerical value as its mass concentration. Different materials usually have different densities, and density may be relevant to buoyancy, purity and packaging. Osmium and iridium are the densest known elements at standard conditions for temperature and pressure. To simplify comparisons of density across different s ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Jupiter Radius
The Jupiter radius or Jovian radius ( or ) has a value of , or 11.2 Earth radii () (one Earth radius equals ). The Jupiter radius is a unit of length used in astronomy to describe the radii of gas giants and some extrasolar planets. It is also used in describing brown dwarfs. In 2015, the International Astronomical Union defined the ''nominal equatorial Jovian radius'' to remain constant regardless of subsequent improvements in measurement precision of . This constant is defined as exactly: :\mathcal^\mathrm N_\mathrm = Similarly, the ''nominal polar Jovian radius'' is defined to be exactly: :\mathcal^\mathrm N_\mathrm = These values correspond to the radius of Jupiter at 1 bar of pressure. The common usage is to refer to the equatorial radius, unless the polar radius is specifically needed. Comparison For comparison, one Solar radius is equivalent to: * 400 Lunar radius() * 109 Earth radius () * 9.735 Jupiter radius () References {{Jupiter Planetary science Units ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Radius
In classical geometry, a radius ( : radii) of a circle or sphere is any of the line segments from its center to its perimeter, and in more modern usage, it is also their length. The name comes from the latin ''radius'', meaning ray but also the spoke of a chariot wheel. as a function of axial position ../nowiki>" Spherical coordinates In a spherical coordinate system, the radius describes the distance of a point from a fixed origin. Its position if further defined by the polar angle measured between the radial direction and a fixed zenith direction, and the azimuth angle, the angle between the orthogonal projection of the radial direction on a reference plane that passes through the origin and is orthogonal to the zenith, and a fixed reference direction in that plane. See also *Bend radius *Filling radius in Riemannian geometry *Radius of convergence * Radius of convexity *Radius of curvature *Radius of gyration ''Radius of gyration'' or gyradius of a body about the axis of r ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Jupiter Mass
Jupiter mass, also called Jovian mass, is the unit of mass equal to the total mass of the planet Jupiter. This value may refer to the mass of the planet alone, or the mass of the entire Jovian system to include the moons of Jupiter. Jupiter is by far the most massive planet in the Solar System. It is approximately 2.5 times as massive as all of the other planets in the Solar System combined. Jupiter mass is a common unit of mass in astronomy that is used to indicate the masses of other similarly-sized objects, including the outer planets, extrasolar planets, and brown dwarfs, as this unit provides a convenient scale for comparison. Current best estimates The current best known value for the mass of Jupiter can be expressed as : :M_\mathrm=(1.89813 \pm 0.00019)\times10^ \text, which is about as massive as the sun (is about ): :M_\mathrm=\frac M_ \approx (9.547919 \pm 0.000002) \times10^ M_. Jupiter is 318 times as massive as Earth: :M_\mathrm = 3.1782838 \times 10^2 M_\oplu ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |