|
Kawasaki's Riemann–Roch Formula
Kawasaki disease (also known as mucocutaneous lymph node syndrome) is a syndrome of unknown cause that results in a fever and mainly affects children under 5 years of age. It is a form of vasculitis, in which medium-sized blood vessels become inflamed throughout the body. The fever typically lasts for more than five days and is not affected by antipyretics, usual medications. Other common symptoms include lymphadenopathy, large lymph nodes in the neck, a rash in the genital area, lips, Palm (hands), palms, or soles of the feet, and red eye (medicine), red eyes. Within three weeks of the onset, the skin from the hands and feet may peel, after which recovery typically occurs. The disease is the leading cause of acquired heart disease in children in developed countries, which include the formation of coronary artery aneurysms and myocarditis. While the specific cause is unknown, it is thought to result from an excessive immune response to particular infections in children who are G ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Pediatrics
Pediatrics (American English) also spelled paediatrics (British English), is the branch of medicine that involves the medical care of infants, children, Adolescence, adolescents, and young adults. In the United Kingdom, pediatrics covers many of their youth until the age of 18. The American Academy of Pediatrics recommends people seek pediatric care through the age of 21, but some pediatric subspecialists continue to care for adults up to 25. Worldwide age limits of pediatrics have been trending upward year after year. A physician, medical doctor who specializes in this area is known as a pediatrician, or paediatrician. The word ''pediatrics'' and its cognates mean "healer of children", derived from the two Ancient Greek, Greek words: (''pais'' "child") and (''iatros'' "doctor, healer"). Pediatricians work in clinics, research centers, universities, general hospitals and children's hospitals, including those who practice pediatric subspecialties (e.g. neonatology requires reso ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Antipyretics
An antipyretic (, from ''anti-'' 'against' and ' 'feverish') is a substance that reduces fever. Antipyretics cause the hypothalamus to override a prostaglandin-induced increase in temperature. The body then works to lower the temperature, which results in a reduction in fever. Most antipyretic medications have other purposes. The most common antipyretics in the US are usually ibuprofen and aspirin, which are nonsteroidal anti-inflammatory drugs (NSAIDs) used primarily as anti-inflammatories and analgesics (pain relievers), but which also have antipyretic properties; and paracetamol (acetaminophen), an analgesic without anti-inflammatory properties. There is some debate over the appropriate use of such medications, since fever is part of the body's immune response to infection. A study published by the Royal Society claims that fever suppression causes at least 1% more influenza deaths in the United States, or 700 extra deaths per year. Non-pharmacological treatment Bathing or ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Aspirin
Aspirin () is the genericized trademark for acetylsalicylic acid (ASA), a nonsteroidal anti-inflammatory drug (NSAID) used to reduce pain, fever, and inflammation, and as an antithrombotic. Specific inflammatory conditions that aspirin is used to treat include Kawasaki disease, pericarditis, and rheumatic fever. Aspirin is also used long-term to help prevent further heart attacks, ischaemic strokes, and blood clots in people at high risk. For pain or fever, effects typically begin within 30 minutes. Aspirin works similarly to other NSAIDs but also suppresses the normal functioning of platelets. One common adverse effect is an upset stomach. More significant side effects include stomach ulcers, stomach bleeding, and worsening asthma. Bleeding risk is greater among those who are older, drink alcohol, take other NSAIDs, or are on other blood thinners. Aspirin is not recommended in the last part of pregnancy. It is not generally recommended in children with infections ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
COVID-19
Coronavirus disease 2019 (COVID-19) is a contagious disease caused by the coronavirus SARS-CoV-2. In January 2020, the disease spread worldwide, resulting in the COVID-19 pandemic. The symptoms of COVID‑19 can vary but often include fever, fatigue, cough, breathing difficulties, anosmia, loss of smell, and ageusia, loss of taste. Symptoms may begin one to fourteen days incubation period, after exposure to the virus. At least a third of people who are infected asymptomatic, do not develop noticeable symptoms. Of those who develop symptoms noticeable enough to be classified as patients, most (81%) develop mild to moderate symptoms (up to mild pneumonia), while 14% develop severe symptoms (dyspnea, hypoxia (medical), hypoxia, or more than 50% lung involvement on imaging), and 5% develop critical symptoms (respiratory failure, shock (circulatory), shock, or organ dysfunction, multiorgan dysfunction). Older people have a higher risk of developing severe symptoms. Some complicati ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Multisystem Inflammatory Syndrome In Children
Multisystem inflammatory syndrome in children (MIS-C), or paediatric inflammatory multisystem syndrome (PIMS / PIMS-TS), or systemic inflammatory syndrome in COVID-19 (SISCoV), is a rare systemic illness involving persistent fever and extreme inflammation following exposure to SARS-CoV-2, the virus responsible for COVID-19. Studies suggest that MIS-C occurred in 31.6 out of 100,000 people under 21 who were infected with COVID-19. MIS-C has also been monitored as a potential, rare pediatric adverse event following COVID-19 vaccination. Research suggests that COVID-19 vaccination lowers the risk of MIS-C, and in cases where symptoms develop after vaccine, is likely extremely rare or related to factors like recent exposure to COVID-19. It can rapidly lead to medical emergencies such as insufficient blood flow around the body (a condition known as shock). Failure of one or more organs can occur. A warning sign is unexplained persistent fever with severe symptoms following exposu ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Scarlet Fever
Scarlet fever, also known as scarlatina, is an infectious disease caused by ''Streptococcus pyogenes'', a Group A streptococcus (GAS). It most commonly affects children between five and 15 years of age. The signs and symptoms include a sore throat, fever, headache, cervical lymphadenopathy, swollen lymph nodes, and a characteristic rash. The face is flushed and the Exanthem, rash is Erythema, red and Blanch (medical), blanching. It typically feels like sandpaper and the tongue may be red and bumpy. The rash occurs as a result of capillary damage by exotoxins produced by ''S.pyogenes''. On darker-pigmented skin the rash may be hard to discern. Scarlet fever develops in a small number of people who have strep throat or streptococcal skin infections. The bacteria are usually spread by people coughing or sneezing. It can also be spread when a person touches an object that has the bacteria on it and then touches their mouth or nose. The diagnosis is typically confirmed by throat ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
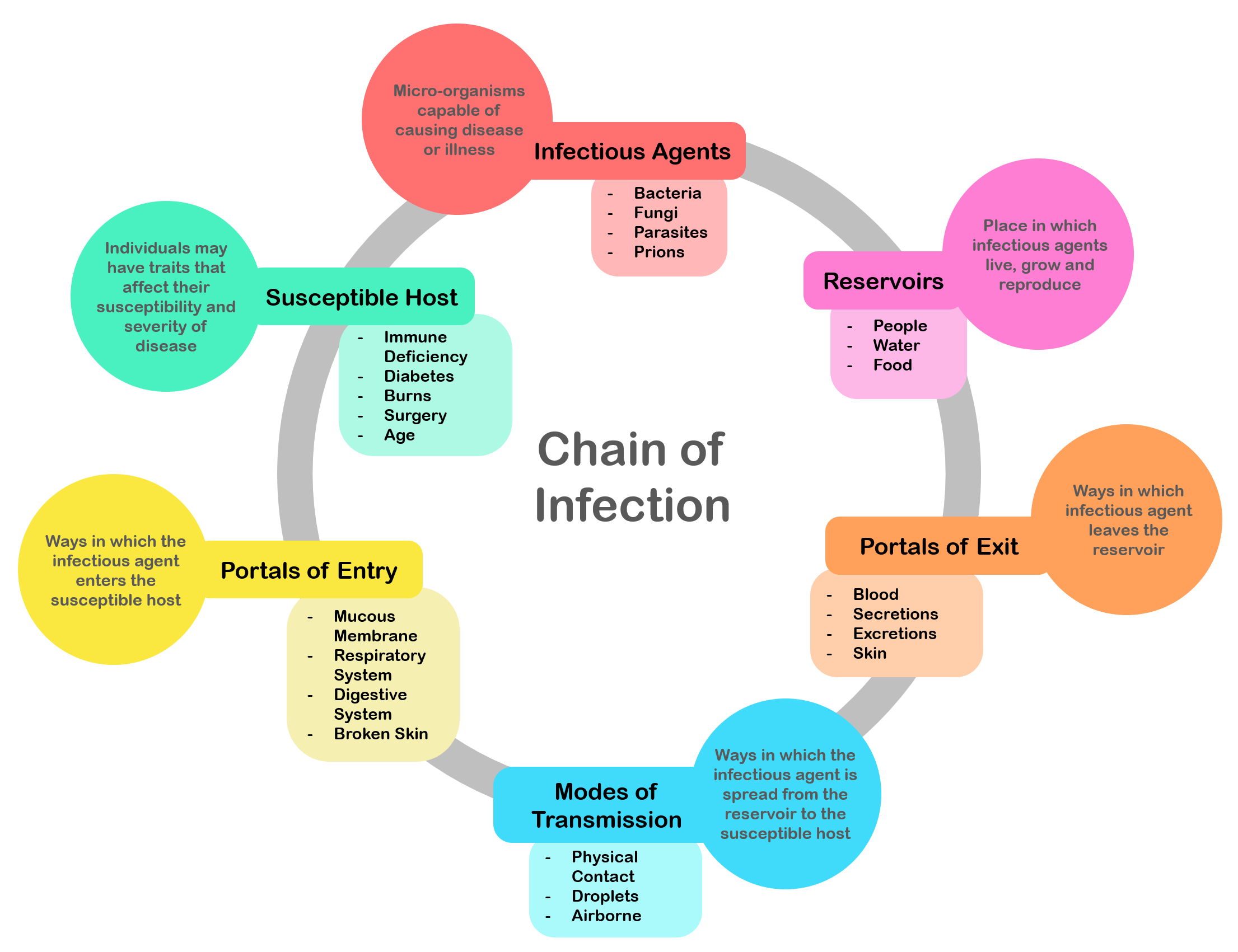
Infectious Disease
An infection is the invasion of tissue (biology), tissues by pathogens, their multiplication, and the reaction of host (biology), host tissues to the infectious agent and the toxins they produce. An infectious disease, also known as a transmissible disease or communicable disease, is an Disease#Terminology, illness resulting from an infection. Infections can be caused by a wide range of pathogens, most prominently pathogenic bacteria, bacteria and viruses. Hosts can fight infections using their immune systems. Mammalian hosts react to infections with an Innate immune system, innate response, often involving inflammation, followed by an Adaptive immune system, adaptive response. Treatment for infections depends on the type of pathogen involved. Common medications include: * Antibiotics for bacterial infections. * Antivirals for viral infections. * Antifungals for fungal infections. * Antiprotozoals for protozoan infections. * Antihelminthics for infections caused by parasi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Genetic Susceptibility
Public health genomics is the use of genomics information to benefit public health. This is visualized as more effective preventive care and disease treatments with better specificity, tailored to the genetic makeup of each patient. According to the Centers for Disease Control and Prevention (U.S.), Public Health genomics is an emerging field of study that assesses the impact of genes and their interaction with behavior, diet and the environment on the population's health. This field of public health genomics is less than a decade old. A number of think tanks, universities, and governments (including the U.S., UK, and Australia) have started public health genomics projects. Research on the human genome is generating new knowledge that is changing public health programs and policies. Advances in genomic sciences are increasingly being used to improve health, prevent disease, educate and train the public health workforce, other healthcare providers, and citizens. Public policy Pu ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Infection
An infection is the invasion of tissue (biology), tissues by pathogens, their multiplication, and the reaction of host (biology), host tissues to the infectious agent and the toxins they produce. An infectious disease, also known as a transmissible disease or communicable disease, is an Disease#Terminology, illness resulting from an infection. Infections can be caused by a wide range of pathogens, most prominently pathogenic bacteria, bacteria and viruses. Hosts can fight infections using their immune systems. Mammalian hosts react to infections with an Innate immune system, innate response, often involving inflammation, followed by an Adaptive immune system, adaptive response. Treatment for infections depends on the type of pathogen involved. Common medications include: * Antibiotics for bacterial infections. * Antivirals for viral infections. * Antifungals for fungal infections. * Antiprotozoals for protozoan infections. * Antihelminthics for infections caused by parasi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Immune Response
An immune response is a physiological reaction which occurs within an organism in the context of inflammation for the purpose of defending against exogenous factors. These include a wide variety of different toxins, viruses, intra- and extracellular bacteria, protozoa, Parasitic worm, helminths, and Fungus, fungi which could cause serious problems to the health of the host organism if not cleared from the body. In addition, there are other forms of immune response. For example, harmless exogenous factors (such as pollen and food components) can trigger allergy; latex and metals are also known allergens. A transplanted tissue (for example, blood) or organ can cause graft-versus-host disease. A type of immune reactivity known as Rh disease can be observed in pregnant women. These special forms of immune response are classified as hypersensitivity. Another special form of immune response is CD4+ T cells and antitumor immunity, antitumor immunity. In general, there are two branches of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Myocarditis
Myocarditis is inflammation of the cardiac muscle. Myocarditis can progress to inflammatory cardiomyopathy when there is associated ventricular remodeling and cardiac dysfunction due to chronic inflammation. Symptoms can include shortness of breath, chest pain, Exercise intolerance, decreased ability to exercise, and an irregular heartbeat. The duration of problems can vary from hours to months. Complications may include heart failure, due to dilated cardiomyopathy or cardiac arrest. Myocarditis is most often due to a viral infection. Other causes include bacterial infections, certain medications, toxins and autoimmune disorders. A diagnosis may be supported by an electrocardiogram (ECG), increased troponin, cardiac magnetic resonance imaging, heart MRI, and occasionally a heart biopsy. An echocardiogram, ultrasound of the heart is important to rule out other potential causes, such as valvular heart disease, heart valve problems. Treatment depends on both the severity and the c ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Coronary Artery Aneurysm
Coronary artery aneurysm is an abnormal dilatation of part of the coronary artery. This rare disorder occurs in about 0.3–4.9% of patients who undergo coronary angiography. Signs and symptoms The majority of individuals suffering from coronary artery aneurysms do not exhibit any symptoms; the development of complications or concurrent atherosclerotic coronary artery disease is what causes clinical manifestations to occur. The most common complications include coronary spasm, distal embolization, aneurysm rupture, local thrombosis, and compression of surrounding structures due to massive enlargement of coronary artery aneurysm. Causes Acquired causes include atherosclerosis in adults, Kawasaki disease in children and coronary catheterization. With the invention of drug eluting stents, there has been more cases implying stents lead to coronary aneurysms. The pathophysiology, although not completely understood, might be comparable to that of aneurysms of larger vessels. This ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |