|
Karplus–Strong String Synthesis
Karplus–Strong string synthesis is a method of physical modelling synthesis that loops a short waveform through a filtered delay line to simulate the sound of a hammered or plucked string instrument, string or some types of Percussion instrument, percussion. At first glance, this technique can be viewed as subtractive synthesis based on a feedback loop similar to that of a comb filter for z-transform analysis. However, it can also be viewed as the simplest class of Table-lookup synthesis, wavetable-modification algorithms now known as digital waveguide synthesis, because the delay line acts to store one period of the signal. Alexander Strong invented the algorithm, and Kevin Karplus did the first analysis of how it worked. Together they developed software and hardware implementations of the algorithm, including a custom VLSI chip. They named the algorithm "Digitar" synthesis, as a portmanteau for "digital guitar". How it works # A short excitation waveform (of length L s ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Physical Modelling Synthesis
Physical modelling synthesis refers to sound synthesis methods in which the waveform of the sound to be generated is computed using a mathematical model, a set of equations and algorithms to simulate a physical source of sound, usually a musical instrument. General methodology Modelling attempts to replicate laws of physics that govern sound production, and will typically have several parameters, some of which are constants that describe the physical materials and dimensions of the instrument, while others are time-dependent functions describing the player's interaction with the instrument, such as plucking a string, or covering toneholes. For example, to model the sound of a drum, there would be a mathematical model of how striking the drumhead injects energy into a two-dimensional membrane. Incorporating this, a larger model would simulate the properties of the membrane (mass density, stiffness, etc.), its coupling with the resonance of the cylindrical body of the drum, and ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Chirp
A chirp is a signal in which the frequency increases (''up-chirp'') or decreases (''down-chirp'') with time. In some sources, the term ''chirp'' is used interchangeably with sweep signal. It is commonly applied to sonar, radar, and laser systems, and to other applications, such as in spread-spectrum communications (see chirp spread spectrum). This signal type is biologically inspired and occurs as a phenomenon due to dispersion (a non-linear dependence between frequency and the propagation speed of the wave components). It is usually compensated for by using a matched filter, which can be part of the propagation channel. Depending on the specific performance measure, however, there are better techniques both for radar and communication. Since it was used in radar and space, it has been adopted also for communication standards. For automotive radar applications, it is usually called linear frequency modulated waveform (LFMW). In spread-spectrum usage, surface acoustic wave (S ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
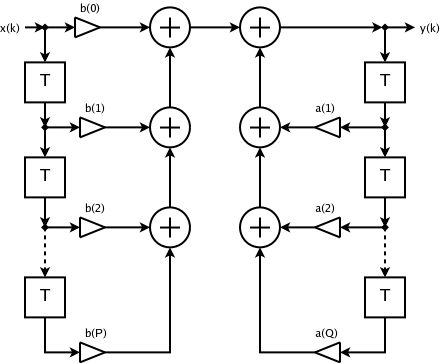
Finite Impulse Response
In signal processing, a finite impulse response (FIR) filter is a filter whose impulse response (or response to any finite length input) is of ''finite'' duration, because it settles to zero in finite time. This is in contrast to infinite impulse response (IIR) filters, which may have internal feedback and may continue to respond indefinitely (usually decaying). The impulse response (that is, the output in response to a Kronecker delta input) of an Nth-order discrete-time FIR filter lasts exactly N+1 samples (from first nonzero element through last nonzero element) before it then settles to zero. FIR filters can be discrete-time or continuous-time, and digital or analog. Definition For a causal discrete-time FIR filter of order ''N'', each value of the output sequence is a weighted sum of the most recent input values: :\begin y &= b_0 x + b_1 x -1+ \cdots + b_N x -N\\ &= \sum_^N b_i\cdot x -i \end where: * x /math> is the input signal, * y /math> is the outpu ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Infinite Impulse Response
Infinite impulse response (IIR) is a property applying to many linear time-invariant systems that are distinguished by having an impulse response h(t) that does not become exactly zero past a certain point but continues indefinitely. This is in contrast to a finite impulse response (FIR) system, in which the impulse response ''does'' become exactly zero at times t>T for some finite T, thus being of finite duration. Common examples of linear time-invariant systems are most electronic and digital filters. Systems with this property are known as ''IIR systems'' or ''IIR filters''. In practice, the impulse response, even of IIR systems, usually approaches zero and can be neglected past a certain point. However the physical systems which give rise to IIR or FIR responses are dissimilar, and therein lies the importance of the distinction. For instance, analog electronic filters composed of resistors, capacitors, and/or inductors (and perhaps linear amplifiers) are generally IIR filte ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Interpolation
In the mathematics, mathematical field of numerical analysis, interpolation is a type of estimation, a method of constructing (finding) new data points based on the range of a discrete set of known data points. In engineering and science, one often has a number of data points, obtained by sampling (statistics), sampling or experimentation, which represent the values of a function for a limited number of values of the Dependent and independent variables, independent variable. It is often required to interpolate; that is, estimate the value of that function for an intermediate value of the independent variable. A closely related problem is the function approximation, approximation of a complicated function by a simple function. Suppose the formula for some given function is known, but too complicated to evaluate efficiently. A few data points from the original function can be interpolated to produce a simpler function which is still fairly close to the original. The resulting gai ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Just-noticeable Difference
In the branch of experimental psychology focused on sense, sensation, and perception, which is called psychophysics, a just-noticeable difference or JND is the amount something must be changed in order for a difference to be noticeable, detectable at least half the time. This limen is also known as the difference limen, difference threshold, or least perceptible difference. Quantification For many sensory modalities, over a wide range of stimulus magnitudes sufficiently far from the upper and lower limits of perception, the 'JND' is a fixed proportion of the reference sensory level, and so the ratio of the JND/reference is roughly constant (that is the JND is a constant proportion/percentage of the reference level). Measured in physical units, we have: \frac = k, where I\! is the original intensity of the particular stimulation, \Delta I\! is the addition to it required for the change to be perceived (the JND), and ''k'' is a constant. This rule was first discovered by Erns ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Digital Delay Line
A digital delay line (or simply delay line, also called delay filter) is a discrete element in a digital filter, which allows a signal to be delayed by a number of Sample (signal), samples. Delay lines are commonly used to delay audio signals feeding loudspeakers to compensate for the speed of sound in air, and to align video signals with accompanying audio, called audio-to-video synchronization. Delay lines may compensate for Latency (audio), electronic processing latency so that multiple signals leave a device simultaneously despite having different pathways. Digital delay lines are widely used building blocks in methods to simulate room acoustics, musical instruments and Effects unit, effects units. Digital waveguide synthesis shows how digital delay lines can be used as sound synthesis methods for various musical instruments such as string instruments and wind instruments. If a delay line holds a non-integer value smaller than one, it results in a fractional delay line (also ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |