|
K-theory Of A Stack
In mathematics, K-theory is, roughly speaking, the study of a ring generated by vector bundles over a topological space or scheme. In algebraic topology, it is a cohomology theory known as topological K-theory. In algebra and algebraic geometry, it is referred to as algebraic K-theory. It is also a fundamental tool in the field of operator algebras. It can be seen as the study of certain kinds of invariants of large matrices. K-theory involves the construction of families of ''K''-functors that map from topological spaces or schemes to associated rings; these rings reflect some aspects of the structure of the original spaces or schemes. As with functors to groups in algebraic topology, the reason for this functorial mapping is that it is easier to compute some topological properties from the mapped rings than from the original spaces or schemes. Examples of results gleaned from the K-theory approach include the Grothendieck–Riemann–Roch theorem, Bott periodicity, the Atiy ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mathematics
Mathematics is an area of knowledge that includes the topics of numbers, formulas and related structures, shapes and the spaces in which they are contained, and quantities and their changes. These topics are represented in modern mathematics with the major subdisciplines of number theory, algebra, geometry, and analysis, respectively. There is no general consensus among mathematicians about a common definition for their academic discipline. Most mathematical activity involves the discovery of properties of abstract objects and the use of pure reason to prove them. These objects consist of either abstractions from nature orin modern mathematicsentities that are stipulated to have certain properties, called axioms. A ''proof'' consists of a succession of applications of deductive rules to already established results. These results include previously proved theorems, axioms, andin case of abstraction from naturesome basic properties that are considered true starting points of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Bott Periodicity
In mathematics, the Bott periodicity theorem describes a periodicity in the homotopy groups of classical groups, discovered by , which proved to be of foundational significance for much further research, in particular in K-theory of stable complex vector bundles, as well as the stable homotopy groups of spheres. Bott periodicity can be formulated in numerous ways, with the periodicity in question always appearing as a period-2 phenomenon, with respect to dimension, for the theory associated to the unitary group. See for example topological K-theory. There are corresponding period-8 phenomena for the matching theories, (real number, real) KO-theory and (quaternionic) KSp-theory, associated to the real orthogonal group and the quaternionic symplectic group, respectively. The J-homomorphism is a homomorphism from the homotopy groups of orthogonal groups to stable homotopy groups of spheres, which causes the period 8 Bott periodicity to be visible in the stable homotopy groups of sph ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Fermi Surface
In condensed matter physics, the Fermi surface is the surface in reciprocal space which separates occupied from unoccupied electron states at zero temperature. The shape of the Fermi surface is derived from the periodicity and symmetry of the crystalline lattice and from the occupation of electronic energy bands. The existence of a Fermi surface is a direct consequence of the Pauli exclusion principle, which allows a maximum of one electron per quantum state. The study of the Fermi surfaces of materials is called fermiology. Theory Consider a spin-less ideal Fermi gas of N particles. According to Fermi–Dirac statistics, the mean occupation number of a state with energy \epsilon_i is given by :\langle n_i\rangle =\frac, where, *\left\langle n_i\right\rangle is the mean occupation number of the i^ state *\epsilon_i is the kinetic energy of the i^ state *\mu is the chemical potential (at zero temperature, this is the maximum kinetic energy the particle can have, i.e. Fermi ene ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
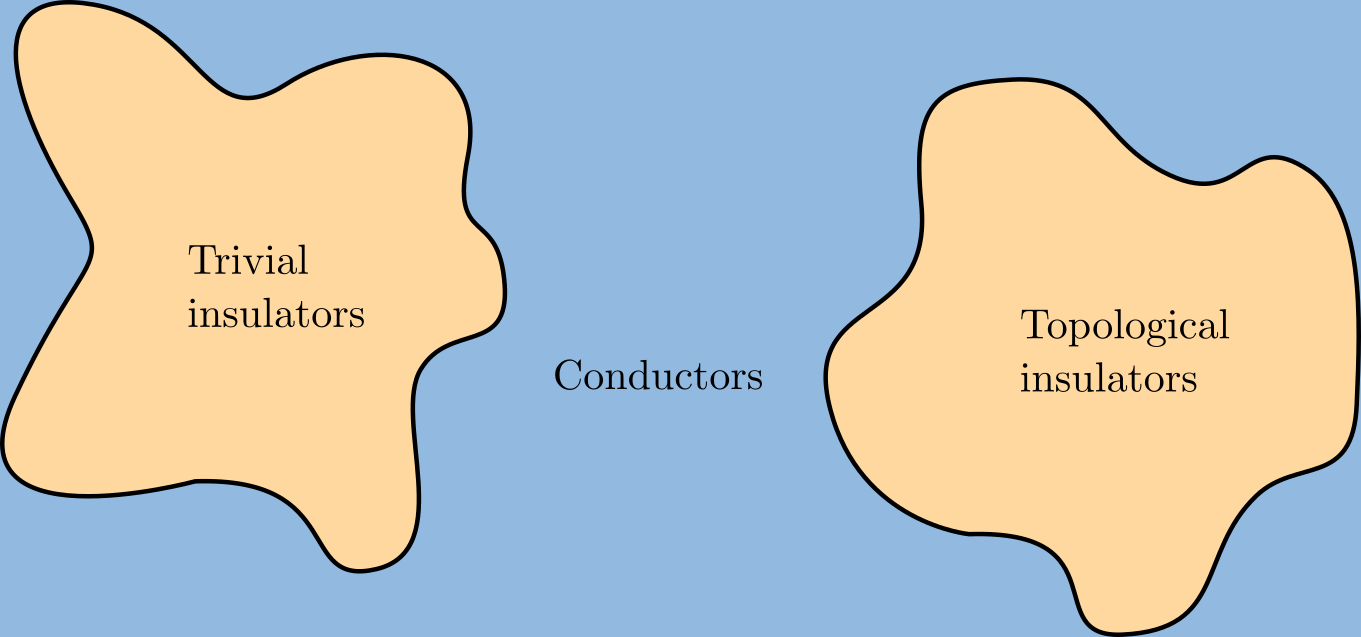
Topological Insulator
A topological insulator is a material whose interior behaves as an electrical insulator while its surface behaves as an electrical conductor, meaning that electrons can only move along the surface of the material. A topological insulator is an insulator for the same reason a "trivial" (ordinary) insulator is: there exists an energy gap between the valence and conduction bands of the material. But in a topological insulator, these bands are, in an informal sense, "twisted", relative to a trivial insulator. The topological insulator cannot be continuously transformed into a trivial one without untwisting the bands, which closes the band gap and creates a conducting state. Thus, due to the continuity of the underlying field, the border of a topological insulator with a trivial insulator (including vacuum, which is topologically trivial) is forced to support a conducting state. Since this results from a global property of the topological insulator's band structure, local (symmetry- ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Condensed Matter Physics
Condensed matter physics is the field of physics that deals with the macroscopic and microscopic physical properties of matter, especially the solid and liquid phases which arise from electromagnetic forces between atoms. More generally, the subject deals with "condensed" phases of matter: systems of many constituents with strong interactions between them. More exotic condensed phases include the superconducting phase exhibited by certain materials at low temperature, the ferromagnetic and antiferromagnetic phases of spins on crystal lattices of atoms, and the Bose–Einstein condensate found in ultracold atomic systems. Condensed matter physicists seek to understand the behavior of these phases by experiments to measure various material properties, and by applying the physical laws of quantum mechanics, electromagnetism, statistical mechanics, and other theories to develop mathematical models. The diversity of systems and phenomena available for study makes condensed matter phy ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Generalized Complex Structure
In the field of mathematics known as differential geometry, a generalized complex structure is a property of a differential manifold that includes as special cases a complex structure and a symplectic structure. Generalized complex structures were introduced by Nigel Hitchin in 2002 and further developed by his students Marco Gualtieri and Gil Cavalcanti. These structures first arose in Hitchin's program of characterizing geometrical structures via functionals of differential forms, a connection which formed the basis of Robbert Dijkgraaf, Sergei Gukov, Andrew Neitzke and Cumrun Vafa's 2004 proposal that topological string theories are special cases of a topological M-theory. Today generalized complex structures also play a leading role in physical string theory, as supersymmetric flux compactifications, which relate 10-dimensional physics to 4-dimensional worlds like ours, require (possibly twisted) generalized complex structures. Definition The generalized tangent bundl ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
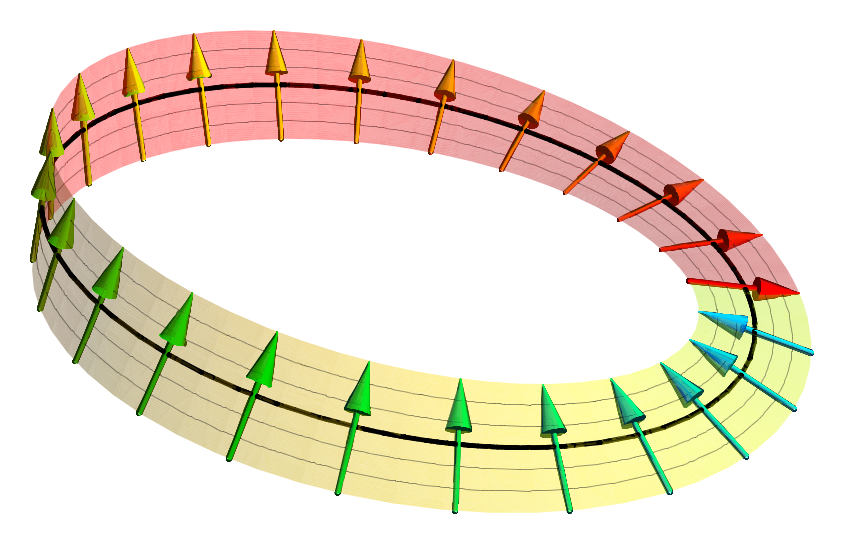
Spinors
In geometry and physics, spinors are elements of a complex vector space that can be associated with Euclidean space. Like geometric vectors and more general tensors, spinors transform linearly when the Euclidean space is subjected to a slight (infinitesimal) rotation. Unlike vectors and tensors, a spinor transforms to its negative when the space is continuously rotated through a complete turn from 0° to 360° (see picture). This property characterizes spinors: spinors can be viewed as the "square roots" of vectors (although this is inaccurate and may be misleading; they are better viewed as "square roots" of sections of vector bundles – in the case of the exterior algebra bundle of the cotangent bundle, they thus become "square roots" of differential forms). It is also possible to associate a substantially similar notion of spinor to Minkowski space, in which case the Lorentz transformations of special relativity play the role of rotations. Spinors were introduced in geome ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Ramond–Ramond Field
In theoretical physics, Ramond–Ramond fields are differential form fields in the 10-dimensional spacetime of type II supergravity theories, which are the classical limits of type II string theory. The ranks of the fields depend on which type II theory is considered. As Joseph Polchinski argued in 1995, D-branes are the charged objects that act as sources for these fields, according to the rules of p-form electrodynamics. It has been conjectured that quantum RR fields are not differential forms, but instead are classified by twisted K-theory. The adjective "Ramond–Ramond" reflects the fact that in the RNS formalism, these fields appear in the Ramond–Ramond sector in which all vector fermions are periodic. Both uses of the word "Ramond" refer to Pierre Ramond, who studied such boundary conditions (the so-called Ramond boundary conditions) and the fields that satisfy them in 1971. Defining the fields The fields in each theory As in Maxwell's theory of electromagnetism and its ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
D-branes
In string theory, D-branes, short for ''Dirichlet membrane'', are a class of extended objects upon which open strings can end with Dirichlet boundary conditions, after which they are named. D-branes were discovered by Jin Dai, Leigh, and Polchinski, and independently by Hořava, in 1989. In 1995, Polchinski identified D-branes with black p-brane solutions of supergravity, a discovery that triggered the Second Superstring Revolution and led to both holographic and M-theory dualities. D-branes are typically classified by their spatial dimension, which is indicated by a number written after the ''D.'' A D0-brane is a single point, a D1-brane is a line (sometimes called a "D-string"), a D2-brane is a plane, and a D25-brane fills the highest-dimensional space considered in bosonic string theory. There are also instantonic D(–1)-branes, which are localized in both space and time. Theoretical background The equations of motion of string theory require that the endpoints of an o ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Type II String Theory
In theoretical physics, type II string theory is a unified term that includes both type IIA strings and type IIB strings theories. Type II string theory accounts for two of the five consistent superstring theories in ten dimensions. Both theories have the maximal amount of supersymmetry — namely 32 supercharges — in ten dimensions. Both theories are based on oriented closed strings. On the worldsheet, they differ only in the choice of GSO projection. Type IIA string theory At low energies, type IIA string theory is described by type IIA supergravity in ten dimensions which is a non-chiral theory (i.e. left–right symmetric) with (1,1) ''d''=10 supersymmetry; the fact that the anomalies in this theory cancel is therefore trivial. In the 1990s it was realized by Edward Witten (building on previous insights by Michael Duff, Paul Townsend, and others) that the limit of type IIA string theory in which the string coupling goes to infinity becomes a new 11-dimensional ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Twisted K-theory
In mathematics, twisted K-theory (also called K-theory with local coefficients) is a variation on K-theory, a mathematical theory from the 1950s that spans algebraic topology, abstract algebra and operator theory. More specifically, twisted K-theory with twist ''H'' is a particular variant of K-theory, in which the twist is given by an integral 3-dimensional cohomology class. It is special among the various twists that K-theory admits for two reasons. First, it admits a geometric formulation. This was provided in two steps; the first one was done in 1970 (Publ. Math. de l' IHÉS) by Peter Donovan and Max Karoubi; the second one in 1988 by Jonathan Rosenberg iContinuous-Trace Algebras from the Bundle Theoretic Point of View In physics, it has been conjectured to classify D-branes, Ramond-Ramond field strengths and in some cases even spinors in type II string theory. For more information on twisted K-theory in string theory, see K-theory (physics). In the broader context of K-the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |