|
J.J. Sylvester
James Joseph Sylvester (3 September 1814 – 15 March 1897) was an English mathematician. He made fundamental contributions to matrix theory, invariant theory, number theory, partition theory, and combinatorics. He played a leadership role in American mathematics in the later half of the 19th century as a professor at the Johns Hopkins University and as founder of the '' American Journal of Mathematics''. At his death, he was a professor at Oxford University. Biography James Joseph was born in London on 3 September 1814, the son of Abraham Joseph, a Jewish merchant. James later adopted the surname Sylvester when his older brother did so upon emigration to the United States—a country which at that time required all immigrants to have a given name, a middle name, and a surname. At the age of 14, Sylvester was a student of Augustus de Morgan at the University of London. His family withdrew him from the University after he was accused of stabbing a fellow stu ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Balls Pond Road Cemetery
Balls Pond Road Cemetery, also known as Jewish (West London Reform) Cemetery, Kingsbury Road Cemetery, Balls Pond Burial Ground and The Jewish Burial Ground, is a Jewish cemetery on Kingsbury Road, Dalston, London N1. It was founded in 1843 and is owned by West London Synagogue. Prominent early members of that place of worship, such as the de Stern, Goldsmid and Mocatta families, are buried in this cemetery. Other notable burials include the ashes of Amy Levy, the first Jewish woman at Cambridge University and the first Jewish woman to be cremated in England. The last burial at the cemetery was in 1951. The cemetery has been Grade II listed since 2020. Notable burials People buried at the cemetery include: * Phinehas Abraham (c.1812–1887), a West Indian merchant born in Jamaica and one of its largest landed proprietors. He was senior justice of the peace for Trelawny Parish in Jamaica and an agent of Lloyd's of London. He was also one of the earliest members of West Lon ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Harry Fielding Reid
Harry Fielding Reid (May 18, 1859 – June 18, 1944) was an American geophysicist. He was notable for his contributions to seismology, particularly his theory of elastic rebound that related faults to earthquakes. Early life Harry Fielding Reid was the fourth child of seven born to Andrew Reid and Fanny Brooke Gwathmey Reid. HF Reid's mother was a descendant of Betty Washington Lewis, sister of the first US President; his father was a successful sugar merchant. The younger Reid's early education took him for at least one year to Switzerland; he is also known to have attended and graduated from the Pennsylvania Military Academy. In 1877 Reid enrolled at the newly founded Johns Hopkins University, from which he earned a B.A. in 1880 as part of the second graduating class. During the following year, he entered the Hopkins Ph.D. program, which was then revolutionizing American scientific and intellectual life. Reid studied under physicist Henry Rowland and mathematician J. J. Sy ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Sylver Coinage
Sylver coinage is a mathematical game for two players, invented by John H. Conway. It is discussed in chapter 18 of '' Winning Ways for Your Mathematical Plays''. This article summarizes that chapter. The two players take turns naming positive integers greater than 1 that are not the sum of nonnegative multiples of previously named integers. The player who cannot name such a number loses. For instance, if player A opens with 2, B can win by naming 3. Sylver coinage is named after James Joseph Sylvester, who proved that if ''a'' and ''b'' are relatively prime positive integers, then (''a'' − 1)(''b'' − 1) − 1 is the largest number that is not a sum of nonnegative multiples of ''a'' and ''b''. Thus, if ''a'' and ''b'' are the first two moves in a game of sylver coinage, this formula gives the largest number that can still be played. More generally, if the greatest common divisor of the moves played so far is ''g'', then only finitely man ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Sylvester's Triangle Problem
Sylvester's theorem or Sylvester's formula describes a particular interpretation of the sum of three pairwise distinct vectors of equal length in the context of triangle geometry. It is also referred to as Sylvester's (triangle) problem in literature, when it is given as a problem rather than a theorem. The theorem is named after the British mathematician James Joseph Sylvester. Theorem Consider three pairwise distinct vectors of equal length \vec, \vec and \vec each of them acting on the same point O thus creating the points A, B and C. Those points form the triangle \triangle ABC with O as the center of its circumcircle. Now let H denote the orthocenter of the triangle, then connection vector \overrightarrow is equal to the sum of the three vectors: :\overrightarrow=\vec+\vec+\vec Furthermore, since the points O and H are located on the Euler line together with the centroid In mathematics and physics, the centroid, also known as geometric center or center of figure, of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Sylvester's Law Of Inertia
Sylvester's law of inertia is a theorem in matrix algebra about certain properties of the coefficient matrix of a real quadratic form that remain invariant under a change of basis. Namely, if ''A'' is the symmetric matrix that defines the quadratic form, and ''S'' is any invertible matrix such that ''D'' = ''SAS''T is diagonal, then the number of negative elements in the diagonal of ''D'' is always the same, for all such ''S''; and the same goes for the number of positive elements. This property is named after James Joseph Sylvester who published its proof in 1852. Statement Let ''A'' be a symmetric square matrix of order ''n'' with real entries. Any non-singular matrix ''S'' of the same size is said to transform ''A'' into another symmetric matrix , also of order ''n'', where ''S''T is the transpose of ''S''. It is also said that matrices ''A'' and ''B'' are congruent. If ''A'' is the coefficient matrix of some quadratic form of R''n'', then ''B'' is ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Sylvester–Gallai Theorem
The Sylvester–Gallai theorem in geometry states that every finite set of points in the Euclidean plane has a line that passes through exactly two of the points or a line that passes through all of them. It is named after James Joseph Sylvester, who posed it as a problem in 1893, and Tibor Gallai, who published one of the first proofs of this theorem in 1944. A line that contains exactly two of a set of points is known as an ''ordinary line''. Another way of stating the theorem is that every finite set of points that is not collinear has an ordinary line. According to a strengthening of the theorem, every finite point set (not all on one line) has at least a linear number of ordinary lines. An algorithm can find an ordinary line in a set of n points in time O(n\log n). History The Sylvester–Gallai theorem was posed as a problem by . suggests that Sylvester may have been motivated by a related phenomenon in algebraic geometry, in which the inflection points of a cubic curve i ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Sylvester Matrix
In mathematics, a Sylvester matrix is a matrix associated to two univariate polynomials with coefficients in a field or a commutative ring. The entries of the Sylvester matrix of two polynomials are coefficients of the polynomials. The determinant of the Sylvester matrix of two polynomials is their resultant, which is zero when the two polynomials have a common root (in case of coefficients in a field) or a non-constant common divisor (in case of coefficients in an integral domain). Sylvester matrices are named after James Joseph Sylvester. Definition Formally, let ''p'' and ''q'' be two nonzero polynomials, respectively of degree ''m'' and ''n''. Thus: :p(z)=p_0+p_1 z+p_2 z^2+\cdots+p_m z^m,\;q(z)=q_0+q_1 z+q_2 z^2+\cdots+q_n z^n. The Sylvester matrix associated to ''p'' and ''q'' is then the (n+m)\times(n+m) matrix constructed as follows: * if ''n'' > 0, the first row is: :\begin p_m & p_ & \cdots & p_1 & p_0 & 0 & \cdots & 0 \end. * the second row is the first row, shifted ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Sylvester's Formula
In matrix theory, Sylvester's formula or Sylvester's matrix theorem (named after J. J. Sylvester) or Lagrange−Sylvester interpolation expresses an analytic function of a matrix as a polynomial in , in terms of the eigenvalues and eigenvectors of ./ Roger A. Horn and Charles R. Johnson (1991), ''Topics in Matrix Analysis''. Cambridge University Press, Jon F. Claerbout (1976), ''Sylvester's matrix theorem'', a section of ''Fundamentals of Geophysical Data Processing''Online versionat sepwww.stanford.edu, accessed on 2010-03-14. It states that : f(A) = \sum_^k f(\lambda_i) ~A_i ~, where the are the eigenvalues of , and the matrices : A_i \equiv \prod_^k \frac \left(A - \lambda_j I\right) are the corresponding Frobenius covariants of , which are (projection) matrix Lagrange polynomials of . Conditions Sylvester's formula applies for any diagonalizable matrix with distinct eigenvalues, 1, …, ''λ''''k'', and any function defined on some subset of the com ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Sylvester's Sequence
In number theory, Sylvester's sequence is an integer sequence in which each term of the sequence is the product of the previous terms, plus one. The first few terms of the sequence are :2, 3, 7, 43, 1807, 3263443, 10650056950807, 113423713055421844361000443 . Sylvester's sequence is named after James Joseph Sylvester, who first investigated it in 1880. Its values grow doubly exponentially, and the sum of its reciprocals forms a series of unit fractions that converges to 1 more rapidly than any other series of unit fractions. The recurrence by which it is defined allows the numbers in the sequence to be factored more easily than other numbers of the same magnitude, but, due to the rapid growth of the sequence, complete prime factorizations are known only for a few of its terms. Values derived from this sequence have also been used to construct finite Egyptian fraction representations of 1, Sasakian Einstein manifolds, and hard instances for online algorithms. Formal definiti ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
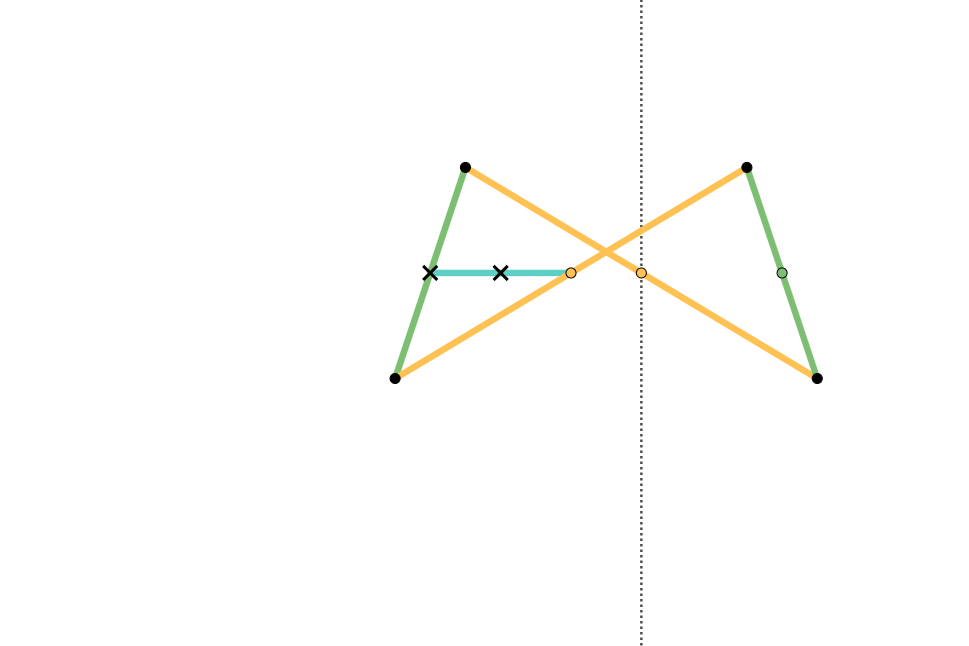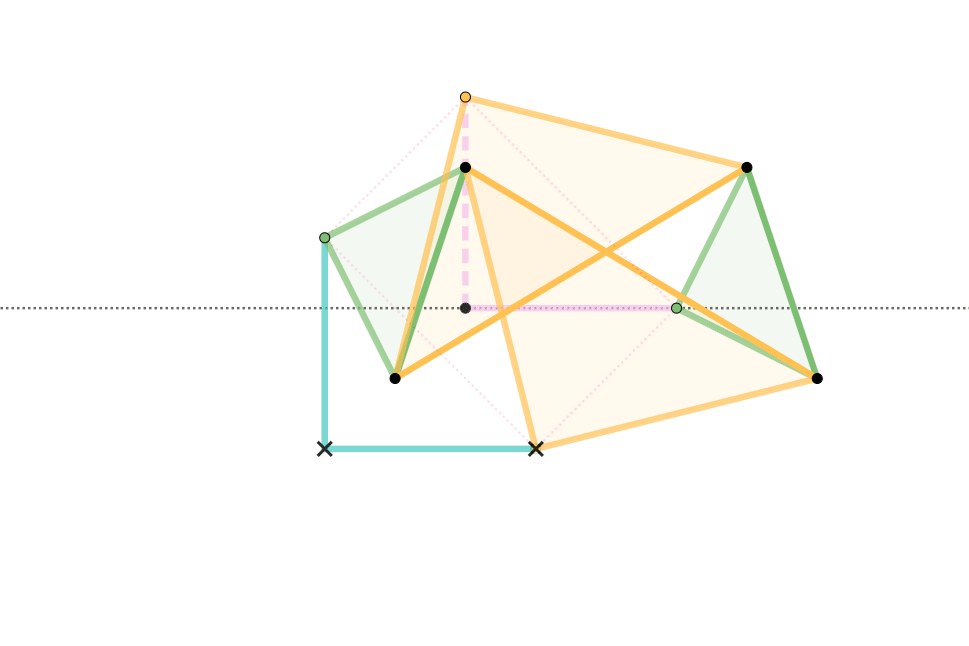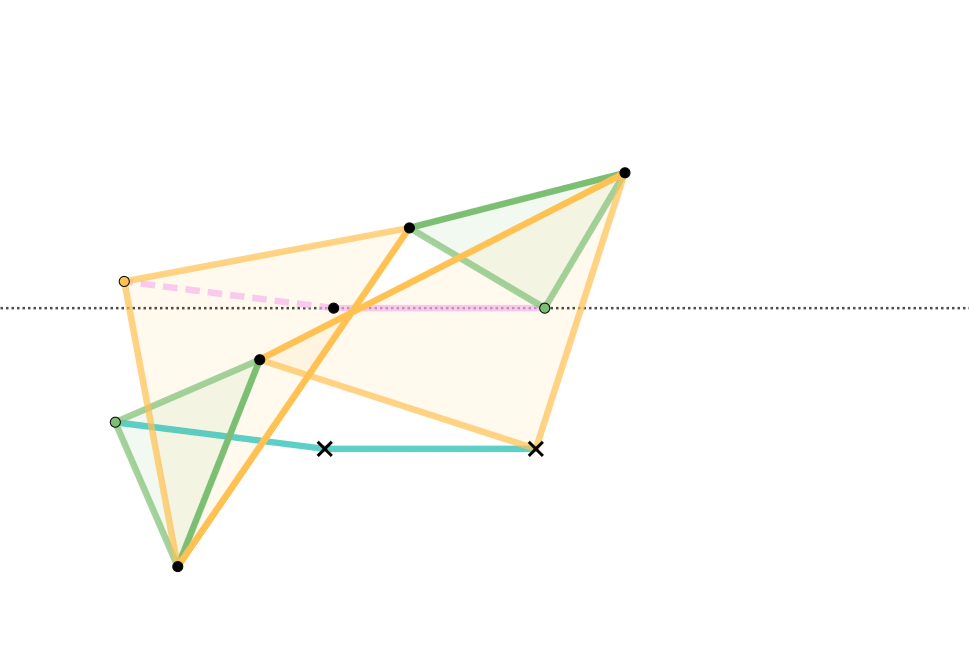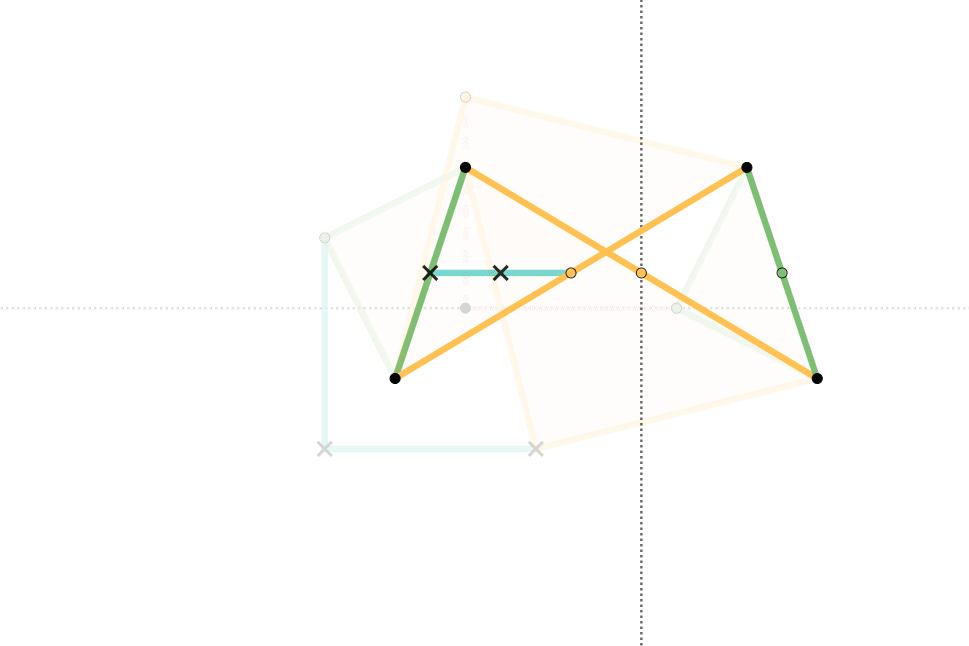
Quadruplanar Inversor
The Quadruplanar inversor of Sylvester and Kempe is a generalization of Hart's inversor. Like Hart's inversor, is a mechanism that provides a perfect straight line motion without sliding guides. The mechanism was described in 1875 by James Joseph Sylvester in the journal Nature. Like Hart's inversor, it is based on an antiparallelogram but the rather than placing the fixed, input and output points on the sides (dividing them in fixed proportion so they are all similar), Sylvester recognized that the additional points could be displaced sideways off the sides, as long as they formed similar triangles. Hart's original form is simply the degenerate case of triangles with altitude zero. Gallery In these diagrams: * The antiparallelogram is highlighted in full opacity links. * Yellow Triangles and Green Triangles are similar. ** Green Triangles are congruent with each other. ** Yellow Triangles are congruent with each other. * Cyan links and Pink links are congruent. * Dashed lin ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Prime Number Theorem
In mathematics, the prime number theorem (PNT) describes the asymptotic distribution of the prime numbers among the positive integers. It formalizes the intuitive idea that primes become less common as they become larger by precisely quantifying the rate at which this occurs. The theorem was proved independently by Jacques Hadamard and Charles Jean de la Vallée Poussin in 1896 using ideas introduced by Bernhard Riemann (in particular, the Riemann zeta function). The first such distribution found is , where is the prime-counting function (the number of primes less than or equal to ''N'') and is the natural logarithm of . This means that for large enough , the probability that a random integer not greater than is prime is very close to . Consequently, a random integer with at most digits (for large enough ) is about half as likely to be prime as a random integer with at most digits. For example, among the positive integers of at most 1000 digits, about one in 2300 is prime ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |