|
Isomap
Isomap is a nonlinear dimensionality reduction method. It is one of several widely used low-dimensional embedding methods. Isomap is used for computing a quasi-isometric, low-dimensional embedding of a set of high-dimensional data points. The algorithm provides a simple method for estimating the intrinsic geometry of a data manifold based on a rough estimate of each data point’s neighbors on the manifold. Isomap is highly efficient and generally applicable to a broad range of data sources and dimensionalities. Introduction Isomap is one representative of isometric mapping methods, and extends metric multidimensional scaling (MDS) by incorporating the geodesic distances imposed by a weighted graph. To be specific, the classical scaling of metric MDS performs low-dimensional embedding based on the pairwise distance between data points, which is generally measured using straight-line Euclidean distance. Isomap is distinguished by its use of the geodesic distance induced by ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
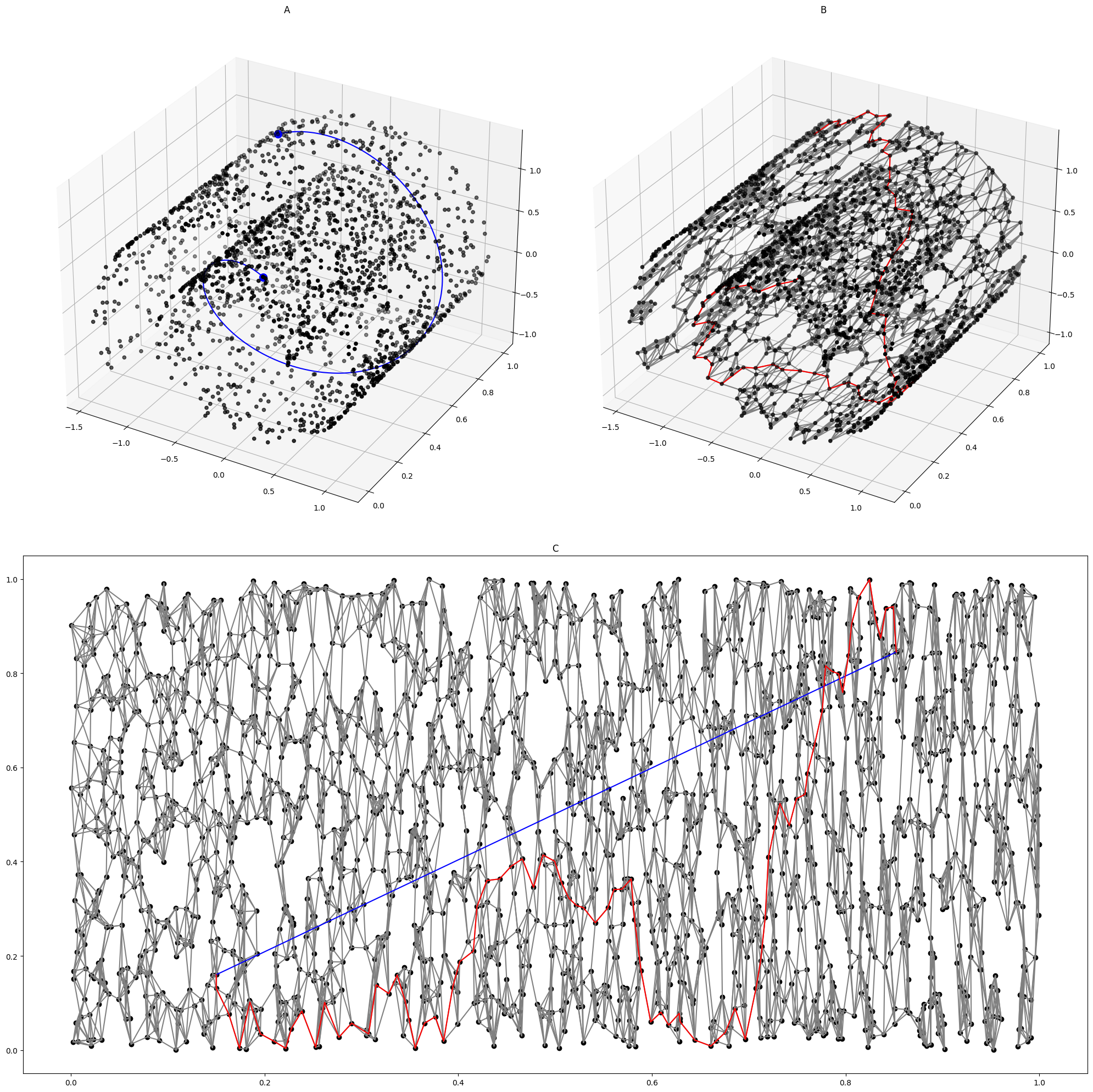
Isomap On Swiss Roll
Isomap is a nonlinear dimensionality reduction method. It is one of several widely used low-dimensional embedding methods. Isomap is used for computing a quasi-isometric, low-dimensional embedding of a set of high-dimensional data points. The algorithm provides a simple method for estimating the intrinsic geometry of a data manifold based on a rough estimate of each data point’s neighbors on the manifold. Isomap is highly efficient and generally applicable to a broad range of data sources and dimensionalities. Introduction Isomap is one representative of isometric mapping methods, and extends metric multidimensional scaling (MDS) by incorporating the geodesic distances imposed by a weighted graph. To be specific, the classical scaling of metric MDS performs low-dimensional embedding based on the pairwise distance between data points, which is generally measured using straight-line Euclidean distance. Isomap is distinguished by its use of the geodesic distance induced by a n ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Nonlinear Dimensionality Reduction
Nonlinear dimensionality reduction, also known as manifold learning, is any of various related techniques that aim to project high-dimensional data, potentially existing across non-linear manifolds which cannot be adequately captured by linear decomposition methods, onto lower-dimensional latent manifolds, with the goal of either visualizing the data in the low-dimensional space, or learning the mapping (either from the high-dimensional space to the low-dimensional embedding or vice versa) itself. The techniques described below can be understood as generalizations of linear decomposition methods used for dimensionality reduction, such as singular value decomposition and principal component analysis. Applications of NLDR High dimensional data can be hard for machines to work with, requiring significant time and space for analysis. It also presents a challenge for humans, since it's hard to visualize or understand data in more than three dimensions. Reducing the dimensionality of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Distance Matrix
In mathematics, computer science and especially graph theory, a distance matrix is a square matrix (two-dimensional array) containing the distances, taken pairwise, between the elements of a set. Depending upon the application involved, the ''distance'' being used to define this matrix may or may not be a metric (mathematics), metric. If there are elements, this matrix will have size . In graph-theoretic applications, the elements are more often referred to as points, nodes or vertices. Non-metric distance matrix In general, a distance matrix is a weighted adjacency matrix of some graph. In a Network (mathematics), network, a directed graph with weights assigned to the arcs, the distance between two nodes of the network can be defined as the minimum of the sums of the weights on the shortest paths joining the two nodes (where the number of steps in the path is bounded). This distance function, while well defined, is not a metric. There need be no restrictions on the weights oth ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Multidimensional Scaling
Multidimensional scaling (MDS) is a means of visualizing the level of similarity of individual cases of a data set. MDS is used to translate distances between each pair of n objects in a set into a configuration of n points mapped into an abstract Cartesian space. More technically, MDS refers to a set of related ordination techniques used in information visualization, in particular to display the information contained in a distance matrix. It is a form of non-linear dimensionality reduction. Given a distance matrix with the distances between each pair of objects in a set, and a chosen number of dimensions, ''N'', an MDS algorithm places each object into ''N''-dimensional space (a lower-dimensional representation) such that the between-object distances are preserved as well as possible. For ''N'' = 1, 2, and 3, the resulting points can be visualized on a scatter plot. Core theoretical contributions to MDS were made by James O. Ramsay of McGill University, who is also ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Principal Component Analysis
Principal component analysis (PCA) is a linear dimensionality reduction technique with applications in exploratory data analysis, visualization and data preprocessing. The data is linearly transformed onto a new coordinate system such that the directions (principal components) capturing the largest variation in the data can be easily identified. The principal components of a collection of points in a real coordinate space are a sequence of p unit vectors, where the i-th vector is the direction of a line that best fits the data while being orthogonal to the first i-1 vectors. Here, a best-fitting line is defined as one that minimizes the average squared perpendicular distance from the points to the line. These directions (i.e., principal components) constitute an orthonormal basis in which different individual dimensions of the data are linearly uncorrelated. Many studies use the first two principal components in order to plot the data in two dimensions and to visually identi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Spectral Clustering
In multivariate statistics, spectral clustering techniques make use of the spectrum (eigenvalues) of the similarity matrix of the data to perform dimensionality reduction before clustering in fewer dimensions. The similarity matrix is provided as an input and consists of a quantitative assessment of the relative similarity of each pair of points in the dataset. In application to image segmentation, spectral clustering is known as segmentation-based object categorization. Definitions Given an enumerated set of data points, the similarity matrix may be defined as a symmetric matrix A, where A_\geq 0 represents a measure of the similarity between data points with indices i and j. The general approach to spectral clustering is to use a standard clustering method (there are many such methods, ''k''-means is discussed below) on relevant eigenvectors of a Laplacian matrix of A. There are many different ways to define a Laplacian which have different mathematical interpretatio ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Kernel PCA
In the field of multivariate statistics, kernel principal component analysis (kernel PCA) is an extension of principal component analysis (PCA) using techniques of kernel methods. Using a kernel, the originally linear operations of PCA are performed in a reproducing kernel Hilbert space. Background: Linear PCA Recall that conventional PCA operates on zero-centered data; that is, :\frac\sum_^N \mathbf_i = \mathbf, where \mathbf_i is one of the N multivariate observations. It operates by diagonalizing the covariance matrix, :C=\frac\sum_^N \mathbf_i\mathbf_i^\top in other words, it gives an eigendecomposition of a matrix, eigendecomposition of the covariance matrix: :\lambda \mathbf=C\mathbf which can be rewritten as :\lambda \mathbf_i^\top \mathbf=\mathbf_i^\top C\mathbf \quad \textrm~i=1,\ldots,N. (See also: Covariance matrix#Covariance matrix as a linear operator, Covariance matrix as a linear operator) Introduction of the Kernel to PCA To understand the utility of kernel PCA, pa ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |