|
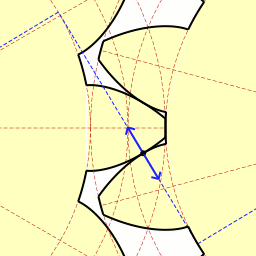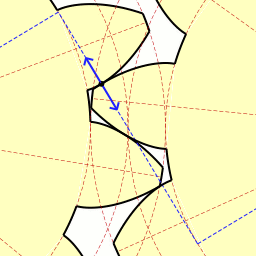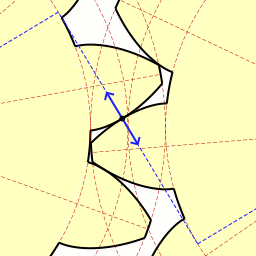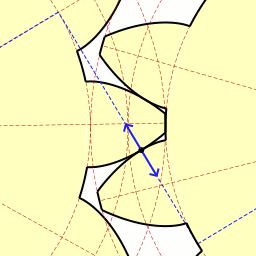
Involute(in Red) Of Parabola(dark Blue)
In mathematics, an involute (also known as an evolvent) is a particular type of curve that is dependent on another shape or curve. An involute of a curve is the Locus (mathematics), locus of a point on a piece of taut string as the string is either unwrapped from or wrapped around the curve. It is a class of curves coming under the Roulette (curve), roulette family of curves. The evolute of an involute is the original curve. The notions of the involute and evolute of a curve were introduced by Christiaan Huygens in his work titled ''Horologium Oscillatorium, Horologium oscillatorium sive de motu pendulorum ad horologia aptato demonstrationes geometricae'' (1673). Involute of a parameterized curve Let \vec c(t),\; t\in [t_1,t_2] be a regular curve in the plane with its Curvature (mathematics), curvature nowhere 0 and a\in (t_1,t_2), then the curve with the parametric representation \vec C_a(t)=\vec c(t) -\frac\; \int_a^t, \vec c'(w), \; dw is an ''involute'' of the g ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Parallel Curve
A parallel of a curve is the envelope of a family of congruent circles centered on the curve. It generalises the concept of '' parallel (straight) lines''. It can also be defined as a curve whose points are at a constant '' normal distance'' from a given curve. These two definitions are not entirely equivalent as the latter assumes smoothness, whereas the former does not. In computer-aided design the preferred term for a parallel curve is offset curve. (In other geometric contexts, the term offset can also refer to translation.) Offset curves are important for example in numerically controlled machining, where they describe for example the shape of the cut made by a round cutting tool of a two-axis machine. The shape of the cut is offset from the trajectory of the cutter by a constant distance in the direction normal to the cutter trajectory at every point. In the area of 2D computer graphics known as vector graphics, the (approximate) computation of parallel curves is ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Involute Gear
The involute gear profile is the most commonly used system for gearing today, with cycloid gearing still used for some specialties such as clocks. In an involute gear, the profiles of the teeth are ''involutes of a circle.'' The involute of a circle is the spiraling curve traced by the end of an imaginary taut string unwinding itself from that stationary circle called the base circle, or (equivalently) a triangle wave projected on the circumference of a circle. The involute gear profile was a fundamental advance in machine design, since unlike with other gear systems, the tooth profile of an involute gear depends only on the number of teeth on the gear, pressure angle, and pitch. That is, a gear's profile does not depend on the gear it mates with. Thus, n and m tooth involute spur gear Spur gears or straight-cut gears are the simplest type of gear. They consist of a cylinder or disk with teeth projecting radially. Viewing the gear at 90 degrees from the shaft length (side on) t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Gear
A gear is a rotating circular machine part having cut teeth or, in the case of a cogwheel or gearwheel, inserted teeth (called ''cogs''), which mesh with another (compatible) toothed part to transmit (convert) torque and speed. The basic principle behind the operation of gears is analogous to the basic principle of levers. A gear may also be known informally as a cog. Geared devices can change the speed, torque, and direction of a power source. Gears of different sizes produce a change in torque, creating a mechanical advantage, through their ''gear ratio'', and thus may be considered a simple machine. The rotational speeds, and the torques, of two meshing gears differ in proportion to their diameters. The teeth on the two meshing gears all have the same shape. Two or more meshing gears, working in a sequence, are called a gear train or a '' transmission''. The gears in a transmission are analogous to the wheels in a crossed, belt pulley system. An advantage of gears is ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Cycloid
In geometry, a cycloid is the curve traced by a point on a circle as it rolls along a straight line without slipping. A cycloid is a specific form of trochoid and is an example of a roulette, a curve generated by a curve rolling on another curve. The cycloid, with the cusps pointing upward, is the curve of fastest descent under uniform gravity (the brachistochrone curve). It is also the form of a curve for which the period of an object in simple harmonic motion (rolling up and down repetitively) along the curve does not depend on the object's starting position (the tautochrone curve). History The cycloid has been called "The Helen of Geometers" as it caused frequent quarrels among 17th-century mathematicians. Historians of mathematics have proposed several candidates for the discoverer of the cycloid. Mathematical historian Paul Tannery cited similar work by the Syrian philosopher Iamblichus as evidence that the curve was known in antiquity. English mathematician ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Tractrix
In geometry, a tractrix (; plural: tractrices) is the curve along which an object moves, under the influence of friction, when pulled on a horizontal plane by a line segment attached to a pulling point (the ''tractor'') that moves at a right angle to the initial line between the object and the puller at an infinitesimal speed. It is therefore a curve of pursuit. It was first introduced by Claude Perrault in 1670, and later studied by Isaac Newton (1676) and Christiaan Huygens (1693). Mathematical derivation Suppose the object is placed at (or in the example shown at right), and the puller at the origin, so is the length of the pulling thread (4 in the example at right). Then the puller starts to move along the axis in the positive direction. At every moment, the thread will be tangent to the curve described by the object, so that it becomes completely determined by the movement of the puller. Mathematically, if the coordinates of the object are , the of the pull ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Catenary
In physics and geometry, a catenary (, ) is the curve that an idealized hanging chain or cable assumes under its own weight when supported only at its ends in a uniform gravitational field. The catenary curve has a U-like shape, superficially similar in appearance to a parabola, which it is not. The curve appears in the design of certain types of arches and as a cross section of the catenoid—the shape assumed by a soap film bounded by two parallel circular rings. The catenary is also called the alysoid, chainette, MathWorld or, particularly in the materials sciences, funicular. Rope statics describes catenaries in a classic statics problem involving a hanging rope. Mathematically, the catenary curve is the graph of the hyperbolic cosine function. The surface of revolution of the catenary curve, the catenoid, is a minimal surface, specifically a minimal surface of revolution. A hanging chain will assume a shape of least potential energy which is a catenary. Galil ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Parallel Curves
A parallel of a curve is the envelope of a family of congruent circles centered on the curve. It generalises the concept of '' parallel (straight) lines''. It can also be defined as a curve whose points are at a constant ''normal distance'' from a given curve. These two definitions are not entirely equivalent as the latter assumes smoothness, whereas the former does not. In computer-aided design the preferred term for a parallel curve is offset curve. (In other geometric contexts, the term offset can also refer to translation.) Offset curves are important for example in numerically controlled machining, where they describe for example the shape of the cut made by a round cutting tool of a two-axis machine. The shape of the cut is offset from the trajectory of the cutter by a constant distance in the direction normal to the cutter trajectory at every point. In the area of 2D computer graphics known as vector graphics, the (approximate) computation of parallel curves is inv ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Parabola
In mathematics, a parabola is a plane curve which is Reflection symmetry, mirror-symmetrical and is approximately U-shaped. It fits several superficially different Mathematics, mathematical descriptions, which can all be proved to define exactly the same curves. One description of a parabola involves a Point (geometry), point (the Focus (geometry), focus) and a Line (geometry), line (the Directrix (conic section), directrix). The focus does not lie on the directrix. The parabola is the locus (mathematics), locus of points in that plane that are equidistant from both the directrix and the focus. Another description of a parabola is as a conic section, created from the intersection of a right circular conical surface and a plane (geometry), plane Parallel (geometry), parallel to another plane that is tangential to the conical surface. The line perpendicular to the directrix and passing through the focus (that is, the line that splits the parabola through the middle) is called th ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Semicubical Parabola
In mathematics, a cuspidal cubic or semicubical parabola is an algebraic plane curve that has an implicit equation of the form : y^2 - a^2 x^3 = 0 (with ) in some Cartesian coordinate system. Solving for leads to the ''explicit form'' : y = \pm a x^, which imply that every real point satisfies . The exponent explains the term ''semicubical parabola''. (A parabola can be described by the equation .) Solving the implicit equation for yields a second ''explicit form'' :x = \left(\frac\right)^. The parametric equation : \quad x = t^2, \quad y = a t^3 can also be deduced from the implicit equation by putting t = \frac. . The semicubical parabolas have a cuspidal singularity; hence the name of ''cuspidal cubic''. The arc length of the curve was calculated by the English mathematician William Neile and published in 1657 (see section History). Properties of semicubical parabolas Similarity Any semicubical parabola (t^2,at^3) is similar to the ''semicubical unit parabola'' ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |