|
Indicated Air Temperature
In aviation, stagnation temperature is known as total air temperature and is measured by a temperature probe mounted on the surface of the aircraft. The probe is designed to bring the air to rest relative to the aircraft. As the air is brought to rest, kinetic energy is converted to internal energy. The air is compressed and experiences an adiabatic increase in temperature. Therefore, total air temperature is higher than the static (or ambient) air temperature. Total air temperature is an essential input to an air data computer in order to enable the computation of static air temperature and hence true airspeed. The relationship between static and total air temperatures is given by: \frac = where: *T_= static air temperature, SAT (kelvins or degrees Rankine) *T_\mathrm= total air temperature, TAT (kelvins or degrees Rankine) *M_= Mach number *\gamma\ =\, ratio of specific heats, approx 1.400 for dry air In practice, the total air temperature probe will not perfectly recover the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Stagnation Temperature
In thermodynamics and fluid mechanics, stagnation temperature is the temperature at a stagnation point in a fluid flow. At a stagnation point the speed of the fluid is zero and all of the kinetic energy has been converted to internal energy and is added to the local static enthalpy. In both compressible and incompressible fluid flow, the stagnation temperature is equal to the ''total temperature'' at all points on the streamline leading to the stagnation point. See gas dynamics. Derivation Adiabatic Stagnation temperature can be derived from the First Law of Thermodynamics. Applying the Steady Flow Energy Equation and ignoring the work, heat and gravitational potential energy terms, we have: :h_0 = h + \frac\, where: :h_0 =\, mass-specific stagnation (or total) enthalpy at a stagnation point :h =\, mass-specific static enthalpy at the point of interest along the stagnation streamline :V =\, velocity at the point of interest along the stagnation streamline Substituting for ent ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Specific Enthalpy
Enthalpy , a property of a thermodynamic system, is the sum of the system's internal energy and the product of its pressure and volume. It is a state function used in many measurements in chemical, biological, and physical systems at a constant pressure, which is conveniently provided by the large ambient atmosphere. The pressure–volume term expresses the work (physics), work required to establish the system's physical dimensions, i.e. to make room for it by displacing its surroundings. The pressure-volume term is very small for solids and liquids at common conditions, and fairly small for gases. Therefore, enthalpy is a stand-in for energy in chemical systems; Bond energy, bond, Lattice energy, lattice, solvation and other "energies" in chemistry are actually enthalpy differences. As a state function, enthalpy depends only on the final configuration of internal energy, pressure, and volume, not on the path taken to achieve it. In the International System of Units (SI), the unit ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Atmospheric Thermodynamics
Atmospheric thermodynamics is the study of heat-to-work transformations (and their reverse) that take place in the earth's atmosphere and manifest as weather or climate. Atmospheric thermodynamics use the laws of classical thermodynamics, to describe and explain such phenomena as the properties of moist air, the formation of clouds, atmospheric convection, boundary layer meteorology, and vertical instabilities in the atmosphere. Atmospheric thermodynamic diagrams are used as tools in the forecasting of storm development. Atmospheric thermodynamics forms a basis for cloud microphysics and convection parameterizations used in numerical weather models and is used in many climate considerations, including convective-equilibrium climate models. Overview The atmosphere is an example of a non-equilibrium system. Atmospheric thermodynamics describes the effect of buoyant forces that cause the rise of less dense (warmer) air, the descent of more dense air, and the transformation of water ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Specific Enthalpy
Enthalpy , a property of a thermodynamic system, is the sum of the system's internal energy and the product of its pressure and volume. It is a state function used in many measurements in chemical, biological, and physical systems at a constant pressure, which is conveniently provided by the large ambient atmosphere. The pressure–volume term expresses the work (physics), work required to establish the system's physical dimensions, i.e. to make room for it by displacing its surroundings. The pressure-volume term is very small for solids and liquids at common conditions, and fairly small for gases. Therefore, enthalpy is a stand-in for energy in chemical systems; Bond energy, bond, Lattice energy, lattice, solvation and other "energies" in chemistry are actually enthalpy differences. As a state function, enthalpy depends only on the final configuration of internal energy, pressure, and volume, not on the path taken to achieve it. In the International System of Units (SI), the unit ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
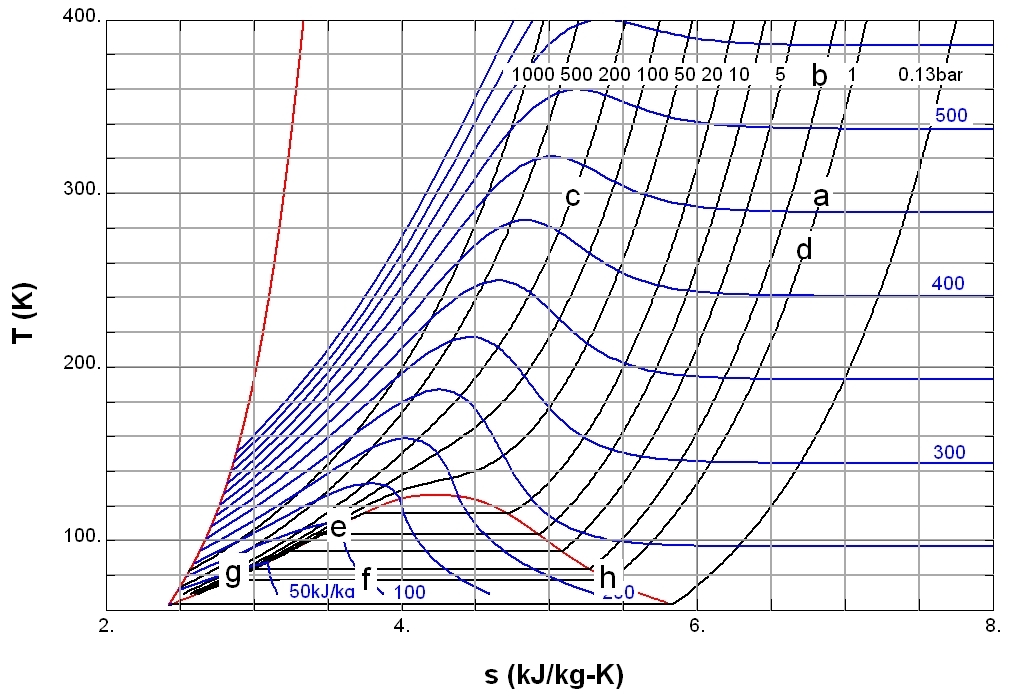
Isentropic Process
In thermodynamics, an isentropic process is an idealized thermodynamic process that is both adiabatic and reversible. The work transfers of the system are frictionless, and there is no net transfer of heat or matter. Such an idealized process is useful in engineering as a model of and basis of comparison for real processes. This process is idealized because reversible processes do not occur in reality; thinking of a process as both adiabatic and reversible would show that the initial and final entropies are the same, thus, the reason it is called isentropic (entropy does not change). Thermodynamic processes are named based on the effect they would have on the system (ex. isovolumetric: constant volume, isenthalpic: constant enthalpy). Even though in reality it is not necessarily possible to carry out an isentropic process, some may be approximated as such. The word "isentropic" can be interpreted in another way, since its meaning is deducible from its etymology. It means a pro ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Speed Of Sound
The speed of sound is the distance travelled per unit of time by a sound wave as it propagates through an elastic medium. At , the speed of sound in air is about , or one kilometre in or one mile in . It depends strongly on temperature as well as the medium through which a sound wave is propagating. At , the speed of sound in air is about . The speed of sound in an ideal gas depends only on its temperature and composition. The speed has a weak dependence on frequency and pressure in ordinary air, deviating slightly from ideal behavior. In colloquial speech, ''speed of sound'' refers to the speed of sound waves in air. However, the speed of sound varies from substance to substance: typically, sound travels most slowly in gases, faster in liquids, and fastest in solids. For example, while sound travels at in air, it travels at in water (almost 4.3 times as fast) and at in iron (almost 15 times as fast). In an exceptionally stiff material such as diamond, sound travels a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Stagnation Temperature
In thermodynamics and fluid mechanics, stagnation temperature is the temperature at a stagnation point in a fluid flow. At a stagnation point the speed of the fluid is zero and all of the kinetic energy has been converted to internal energy and is added to the local static enthalpy. In both compressible and incompressible fluid flow, the stagnation temperature is equal to the ''total temperature'' at all points on the streamline leading to the stagnation point. See gas dynamics. Derivation Adiabatic Stagnation temperature can be derived from the First Law of Thermodynamics. Applying the Steady Flow Energy Equation and ignoring the work, heat and gravitational potential energy terms, we have: :h_0 = h + \frac\, where: :h_0 =\, mass-specific stagnation (or total) enthalpy at a stagnation point :h =\, mass-specific static enthalpy at the point of interest along the stagnation streamline :V =\, velocity at the point of interest along the stagnation streamline Substituting for ent ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Stagnation Point
In fluid dynamics, a stagnation point is a point in a flow field where the local velocity of the fluid is zero.Clancy, L.J. (1975), ''Aerodynamics'', Pitman Publishing Limited, London. A plentiful, albeit surprising, example of such points seem to appear in all but the most extreme cases of fluid dynamics in the form of the "No-slip condition"; the assumption that any portion of a flow field lying along some boundary consists of nothing but stagnation points (the question as to whether this assumption reflects reality or is simply a mathematical convenience has been a continuous subject of debate since the principle was first established). The Bernoulli equation shows that the static pressure is highest when the velocity is zero and hence static pressure is at its maximum value at stagnation points: in this case static pressure equals stagnation pressure. The Bernoulli equation applicable to incompressible flow shows that the stagnation pressure is equal to the dynamic pressure p ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
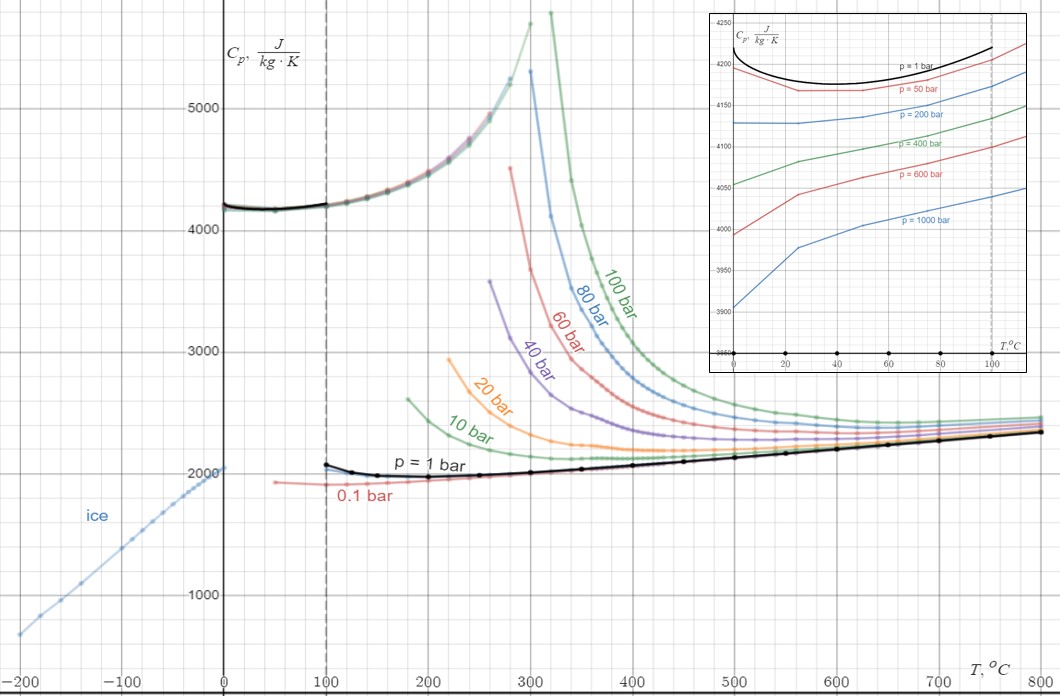
Heat Capacity
Heat capacity or thermal capacity is a physical property of matter, defined as the amount of heat to be supplied to an object to produce a unit change in its temperature. The SI unit of heat capacity is joule per kelvin (J/K). Heat capacity is an extensive property. The corresponding intensive property is the specific heat capacity, found by dividing the heat capacity of an object by its mass. Dividing the heat capacity by the amount of substance in moles yields its molar heat capacity. The volumetric heat capacity measures the heat capacity per volume. In architecture and civil engineering, the heat capacity of a building is often referred to as its thermal mass. Definition Basic definition The heat capacity of an object, denoted by C, is the limit : C = \lim_\frac, where \Delta Q is the amount of heat that must be added to the object (of mass ''M'') in order to raise its temperature by \Delta T. The value of this parameter usually varies considerably depending on the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Gas Constant
The molar gas constant (also known as the gas constant, universal gas constant, or ideal gas constant) is denoted by the symbol or . It is the molar equivalent to the Boltzmann constant, expressed in units of energy per temperature increment per amount of substance, i.e. the pressure–volume product, rather than energy per temperature increment per ''particle''. The constant is also a combination of the constants from Boyle's law, Charles's law, Avogadro's law, and Gay-Lussac's law. It is a physical constant that is featured in many fundamental equations in the physical sciences, such as the ideal gas law, the Arrhenius equation, and the Nernst equation. The gas constant is the constant of proportionality that relates the energy scale in physics to the temperature scale and the scale used for amount of substance. Thus, the value of the gas constant ultimately derives from historical decisions and accidents in the setting of units of energy, temperature and amount of substa ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Heat Capacity Ratio
In thermal physics and thermodynamics, the heat capacity ratio, also known as the adiabatic index, the ratio of specific heats, or Laplace's coefficient, is the ratio of the heat capacity at constant pressure () to heat capacity at constant volume (). It is sometimes also known as the ''isentropic expansion factor'' and is denoted by ( gamma) for an ideal gasγ first appeared in an article by the French mathematician, engineer, and physicist Siméon Denis Poisson: * On p. 332, Poisson defines γ merely as a small deviation from equilibrium which causes small variations of the equilibrium value of the density ρ. In Poisson's article of 1823 – * γ was expressed as a function of density D (p. 8) or of pressure P (p. 9). Meanwhile, in 1816 the French mathematician and physicist Pierre-Simon Laplace had found that the speed of sound depends on the ratio of the specific heats. * However, he didn't denote the ratio as γ. In 1825, Laplace stated that the speed of sound is ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Speed Of Sound
The speed of sound is the distance travelled per unit of time by a sound wave as it propagates through an elastic medium. At , the speed of sound in air is about , or one kilometre in or one mile in . It depends strongly on temperature as well as the medium through which a sound wave is propagating. At , the speed of sound in air is about . The speed of sound in an ideal gas depends only on its temperature and composition. The speed has a weak dependence on frequency and pressure in ordinary air, deviating slightly from ideal behavior. In colloquial speech, ''speed of sound'' refers to the speed of sound waves in air. However, the speed of sound varies from substance to substance: typically, sound travels most slowly in gases, faster in liquids, and fastest in solids. For example, while sound travels at in air, it travels at in water (almost 4.3 times as fast) and at in iron (almost 15 times as fast). In an exceptionally stiff material such as diamond, sound travels a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |


_-_filtered.jpg)