|
Isbell Conjugacy
Isbell conjugacy (a.k.a. Isbell duality or Isbell adjunction) (named after John R. Isbell) is a fundamental construction of enriched category theory formally introduced by William Lawvere in 1986. That is a duality between covariant and contravariant representable presheaves associated with an objects of categories under the Yoneda embedding. Also, says that; "Then the conjugacies are the first step toward expressing the duality between space and quantity fundamental to mathematics". Definition Yoneda embedding The (covariant) Yoneda embedding is a covariant functor from a small category \mathcal into the category of presheaves \left mathcal^, \mathcal \right/math> on \mathcal, taking X \in \mathcal to the contravariant representable functor: Y \; (h^) :\mathcal \rightarrow \left mathcal^, \mathcal \right/math> X \mapsto \mathrm (-,X). and the co-Yoneda embedding (a.k.a. contravariant Yoneda embedding or the dual Yoneda embedding) is a contravariant functor (a covar ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
John R
John R. (born John Richbourg, August 20, 1910 - February 15, 1986) was an American radio disc jockey who attained fame in the 1950s and 1960s for playing rhythm and blues music on Nashville radio station WLAC. He was also a notable record producer and artist manager. Richbourg was arguably the most popular and charismatic of the four announcers at WLAC who showcased popular African-American music in nightly programs from the late 1940s to the early 1970s. (The other three were Gene Nobles, Herman Grizzard, and Bill "Hoss" Allen.) Later rock music disc jockeys, such as Alan Freed and Wolfman Jack, mimicked Richbourg's practice of using speech that simulated African-American street language of the mid-twentieth century. Richbourg's highly stylized approach to on-air presentation of both music and advertising earned him popularity, but it also created identity confusion. Because Richbourg and fellow disc jockey Allen used African-American speech patterns, many listeners thought that ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Isbell Duality
Isbell conjugacy (a.k.a. Isbell duality or Isbell adjunction) (named after John R. Isbell John Rolfe Isbell (October 27, 1930 – August 6, 2005) was an American mathematician, for many years a professor of mathematics at the University at Buffalo (SUNY). Biography Isbell was born in Portland, Oregon, the son of an army officer from I ...) is a fundamental construction of enriched category theory formally introduced by William Lawvere in 1986. That is a duality between covariant and contravariant representable Presheaf (category theory), presheaves associated with an objects of categories under the Yoneda embedding. Also, says that; "Then the conjugacies are the first step toward expressing the duality between space and quantity fundamental to mathematics". Definition Yoneda embedding The (covariant) Yoneda embedding is a covariant functor from a small category \mathcal into the category of Presheaf (category theory), presheaves \left[\mathcal^, \mathcal \right] on \mathcal, ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Advances In Mathematics
''Advances in Mathematics'' is a peer-reviewed scientific journal covering research on pure mathematics. It was established in 1961 by Gian-Carlo Rota. The journal publishes 18 issues each year, in three volumes. At the origin, the journal aimed at publishing articles addressed to a broader "mathematical community", and not only to mathematicians in the author's field. Herbert Busemann writes, in the preface of the first issue, "The need for expository articles addressing either all mathematicians or only those in somewhat related fields has long been felt, but little has been done outside of the USSR. The serial publication ''Advances in Mathematics'' was created in response to this demand." Abstracting and indexing The journal is abstracted and indexed in: * |
Limit (category Theory)
In category theory, a branch of mathematics, the abstract notion of a limit captures the essential properties of universal constructions such as products, pullbacks and inverse limits. The dual notion of a colimit generalizes constructions such as disjoint unions, direct sums, coproducts, pushouts and direct limits. Limits and colimits, like the strongly related notions of universal properties and adjoint functors, exist at a high level of abstraction. In order to understand them, it is helpful to first study the specific examples these concepts are meant to generalize. Definition Limits and colimits in a category C are defined by means of diagrams in C. Formally, a diagram of shape J in C is a functor from J to C: :F:J\to C. The category J is thought of as an index category, and the diagram F is thought of as indexing a collection of objects and morphisms in C patterned on J. One is most often interested in the case where the category J is a small or even finite category. ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Kan Extension
Kan extensions are universal constructs in category theory, a branch of mathematics. They are closely related to adjoints, but are also related to limits and ends. They are named after Daniel M. Kan, who constructed certain (Kan) extensions using limits in 1960. An early use of (what is now known as) a Kan extension from 1956 was in homological algebra to compute derived functors. In ''Categories for the Working Mathematician'' Saunders Mac Lane titled a section "All Concepts Are Kan Extensions", and went on to write that :The notion of Kan extensions subsumes all the other fundamental concepts of category theory. Kan extensions generalize the notion of extending a function defined on a subset to a function defined on the whole set. The definition, not surprisingly, is at a high level of abstraction. When specialised to posets, it becomes a relatively familiar type of question on constrained optimization. Definition A Kan extension proceeds from the data of three categor ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Adjunction (category Theory)
In mathematics, specifically category theory, adjunction is a relationship that two functors may exhibit, intuitively corresponding to a weak form of equivalence between two related categories. Two functors that stand in this relationship are known as adjoint functors, one being the left adjoint and the other the right adjoint. Pairs of adjoint functors are ubiquitous in mathematics and often arise from constructions of "optimal solutions" to certain problems (i.e., constructions of objects having a certain universal property), such as the construction of a free group on a set in algebra, or the construction of the Stone–Čech compactification of a topological space in topology. By definition, an adjunction between categories \mathcal and \mathcal is a pair of functors (assumed to be covariant) :F: \mathcal \rightarrow \mathcal and G: \mathcal \rightarrow \mathcal and, for all objects X in \mathcal and Y in \mathcal a bijection between the respective morphis ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Closed Monoidal Category
In mathematics, especially in category theory, a closed monoidal category (or a ''monoidal closed category'') is a category that is both a monoidal category and a closed category in such a way that the structures are compatible. A classic example is the category of sets, Set, where the monoidal product of sets A and B is the usual cartesian product A \times B, and the internal Hom B^A is the set of functions from A to B. A non- cartesian example is the category of vector spaces, ''K''-Vect, over a field K. Here the monoidal product is the usual tensor product of vector spaces, and the internal Hom is the vector space of linear maps from one vector space to another. The internal language of closed symmetric monoidal categories is linear logic and the type system is the linear type system. Many examples of closed monoidal categories are symmetric. However, this need not always be the case, as non-symmetric monoidal categories can be encountered in category-theoretic formulatio ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
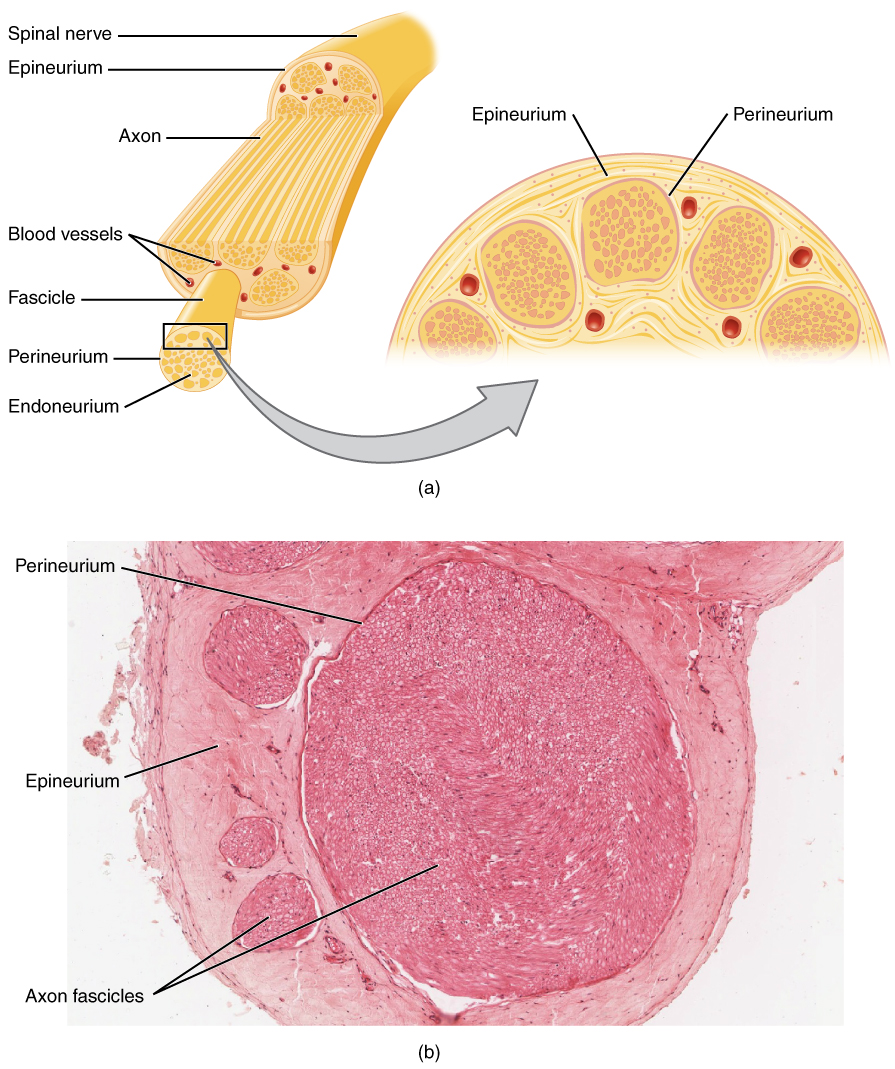
Nerve And Realization (ver
A nerve is an enclosed, cable-like bundle of nerve fibers (called axons) in the peripheral nervous system. A nerve transmits electrical impulses. It is the basic unit of the peripheral nervous system. A nerve provides a common pathway for the electrochemical nerve impulses called action potentials that are transmitted along each of the axons to peripheral organs or, in the case of sensory nerves, from the periphery back to the central nervous system. Each axon, within the nerve, is an extension of an individual neuron, along with other supportive cells such as some Schwann cells that coat the axons in myelin. Within a nerve, each axon is surrounded by a layer of connective tissue called the endoneurium. The axons are bundled together into groups called fascicles, and each fascicle is wrapped in a layer of connective tissue called the perineurium. Finally, the entire nerve is wrapped in a layer of connective tissue called the epineurium. Nerve cells (often called neurons) are f ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Contravariant Functor
In mathematics, specifically category theory, a functor is a mapping between categories. Functors were first considered in algebraic topology, where algebraic objects (such as the fundamental group) are associated to topological spaces, and maps between these algebraic objects are associated to continuous maps between spaces. Nowadays, functors are used throughout modern mathematics to relate various categories. Thus, functors are important in all areas within mathematics to which category theory is applied. The words ''category'' and ''functor'' were borrowed by mathematicians from the philosophers Aristotle and Rudolf Carnap, respectively. The latter used ''functor'' in a linguistic context; see function word. Definition Let ''C'' and ''D'' be categories. A functor ''F'' from ''C'' to ''D'' is a mapping that * associates each object X in ''C'' to an object F(X) in ''D'', * associates each morphism f \colon X \to Y in ''C'' to a morphism F(f) \colon F(X) \to F(Y) in ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Enriched Category Theory
In category theory, a branch of mathematics, an enriched category generalizes the idea of a category by replacing hom-sets with objects from a general monoidal category. It is motivated by the observation that, in many practical applications, the hom-set often has additional structure that should be respected, e.g., that of being a vector space of morphisms, or a topological space of morphisms. In an enriched category, the set of morphisms (the hom-set) associated with every pair of objects is replaced by an object in some fixed monoidal category of "hom-objects". In order to emulate the (associative) composition of morphisms in an ordinary category, the hom-category must have a means of composing hom-objects in an associative manner: that is, there must be a binary operation on objects giving us at least the structure of a monoidal category, though in some contexts the operation may also need to be commutative and perhaps also to have a right adjoint (i.e., making the category symm ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Opposite Functor
In mathematics, specifically category theory, a functor is a mapping between categories. Functors were first considered in algebraic topology, where algebraic objects (such as the fundamental group) are associated to topological spaces, and maps between these algebraic objects are associated to continuous maps between spaces. Nowadays, functors are used throughout modern mathematics to relate various categories. Thus, functors are important in all areas within mathematics to which category theory is applied. The words ''category'' and ''functor'' were borrowed by mathematicians from the philosophers Aristotle and Rudolf Carnap, respectively. The latter used ''functor'' in a linguistic context; see function word. Definition Let ''C'' and ''D'' be categories. A functor ''F'' from ''C'' to ''D'' is a mapping that * associates each object X in ''C'' to an object F(X) in ''D'', * associates each morphism f \colon X \to Y in ''C'' to a morphism F(f) \colon F(X) \to F(Y) in ' ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Representable Functor
In mathematics, particularly category theory, a representable functor is a certain functor from an arbitrary category into the category of sets. Such functors give representations of an abstract category in terms of known structures (i.e. sets and functions) allowing one to utilize, as much as possible, knowledge about the category of sets in other settings. From another point of view, representable functors for a category ''C'' are the functors ''given'' with ''C''. Their theory is a vast generalisation of upper sets in posets, and of Cayley's theorem in group theory. Definition Let C be a locally small category and let Set be the category of sets. For each object ''A'' of C let Hom(''A'',–) be the hom functor that maps object ''X'' to the set Hom(''A'',''X''). A functor ''F'' : C → Set is said to be representable if it is naturally isomorphic to Hom(''A'',–) for some object ''A'' of C. A representation of ''F'' is a pair (''A'', Φ) where :Φ : Hom(''A'',&ndash ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |