|
Isaak Moiseevich Yaglom
Isaak Moiseevich Yaglom (russian: Исаа́к Моисе́евич Ягло́м; 6 March 1921 – 17 April 1988) was a Soviet mathematician and author of popular mathematics books, some with his twin Akiva Yaglom. Yaglom received a Ph.D. from Moscow State University in 1945 as student of Veniamin Kagan. As the author of several books, translated into English, that have become academic standards of reference, he has an international stature. His attention to the necessities of learning (pedagogy) make his books pleasing experiences for students. The seven authors of his Russian obituary recount "…the breadth of his interests was truly extraordinary: he was seriously interested in history and philosophy, passionately loved and had a good knowledge of literature and art, often came forward with reports and lectures on the most diverse topics (for example, on Alexander Blok, Anna Akhmatova, and the Dutch painter M. C. Escher), actively took part in the work of the cinema club in Y ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Kharkov
Kharkiv ( uk, Ха́рків, ), also known as Kharkov (russian: Харькoв, ), is the second-largest city and municipality in Ukraine.Kharkiv "never had eastern-western conflicts" '''' (23 October 2014) Located in the northeast of the country, it is the largest city of the historic region. Kharkiv is the of |
Yaroslavl
Yaroslavl ( rus, Ярослáвль, p=jɪrɐˈsɫavlʲ) is a city and the administrative center of Yaroslavl Oblast, Russia, located northeast of Moscow. The historic part of the city is a World Heritage Site, and is located at the confluence of the Volga and the Kotorosl rivers. It is part of the Golden Ring, a group of historic cities northeast of Moscow that have played an important role in Russian history. Population: Geography Location The city lies in the eastern portion of Yaroslavl Oblast. The nearest large towns are Tutayev ( to the northwest), Gavrilov-Yam ( to the south), and Nerekhta ( to the southeast). The historic center of Yaroslavl lies to the north of the mouth of the Kotorosl River on the right bank of the larger Volga River. The city's entire urban area covers around and includes a number of territories south of the Kotorosl and on the left bank of the Volga. With nearly 600,000 residents, Yaroslavl is, by population, the largest town on the Volga unt ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Ministry Of Education (Soviet Union)
The Ministry of Education of the Union of Soviet Socialist Republics (USSR) (russian: Министерство просвещения СССР), formed on 3 August 1966, was one of the most important government offices in the Soviet Union. It was known as the People's Commissariat for Education (russian: Народный комиссариат просвещения), or Narkompros, until 1946. Narkompros was a Soviet agency founded by the State Commission on Education (russian: Государственная комиссия по просвещению) and charged with the administration of public education and most of other issues related to culture. Its first head was Anatoly Lunacharsky. However he described Nadezhda Krupskaya as the "soul of Narkompros". Mikhail Pokrovsky and Evgraf Litkens also played important roles. Lunacharsky protected most of the avant-garde artists such as Vladimir Mayakovsky, Kazimir Malevich, Vladimir Tatlin and Vsevolod Meyerhold. Despite his effo ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Textbook
A textbook is a book containing a comprehensive compilation of content in a branch of study with the intention of explaining it. Textbooks are produced to meet the needs of educators, usually at educational institutions. Schoolbooks are textbooks and other books used in schools. Today, many textbooks are published in both print and digital formats. History The history of textbooks dates back to ancient civilizations. For example, Ancient Greeks wrote educational texts. The modern textbook has its roots in the mass production made possible by the printing press. Johannes Gutenberg himself may have printed editions of ''Ars Minor'', a schoolbook on Latin grammar by Aelius Donatus. Early textbooks were used by tutors and teachers (e.g. alphabet books), as well as by individuals who taught themselves. The Greek philosopher Socrates lamented the loss of knowledge because the media of transmission were changing. Before the invention of the Greek alphabet 2,500 years ago, knowledge ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Routh's Theorem
In geometry, Routh's theorem determines the ratio of areas between a given triangle and a triangle formed by the pairwise intersections of three cevians. The theorem states that if in triangle ABC points D, E, and F lie on segments BC, CA, and AB, then writing \tfrac = x, \tfrac = y, and \tfrac = z, the signed area of the triangle formed by the cevians AD, BE, and CF is : S_ \frac, where S_ is the area of the triangle ABC. This theorem was given by Edward John Routh on page 82 of his ''Treatise on Analytical Statics with Numerous Examples'' in 1896. The particular case x = y = z = 2 has become popularized as the one-seventh area triangle. The x = y = z = 1 case implies that the three medians are concurrent (through the centroid). Proof Suppose that the area of triangle ABC is 1. For triangle ABD and line FRC using Menelaus's theorem, We could obtain: :\frac \times \frac \times \frac = 1 Then \frac = \frac \times \frac = \frac So the area of triangle ARC is: :S_ = \frac S_ = ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
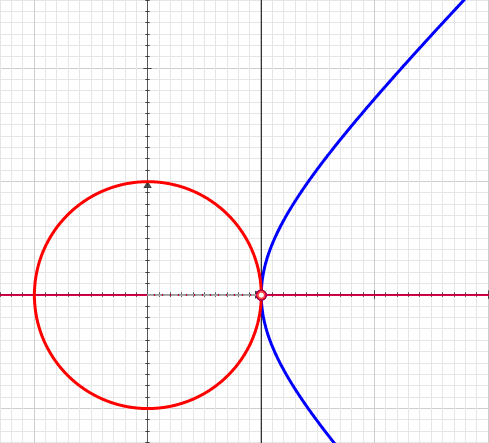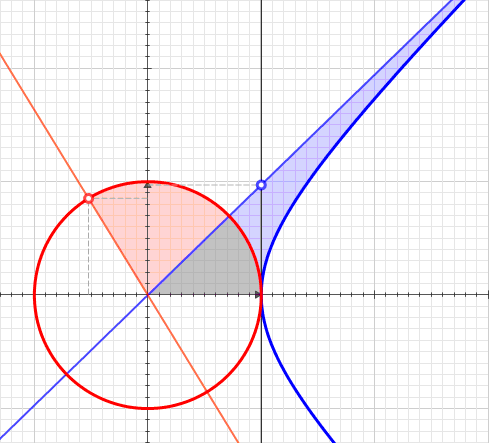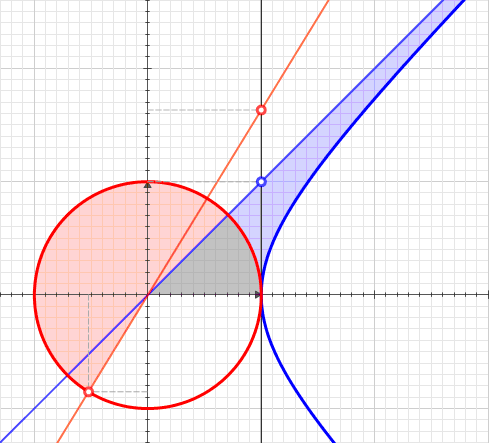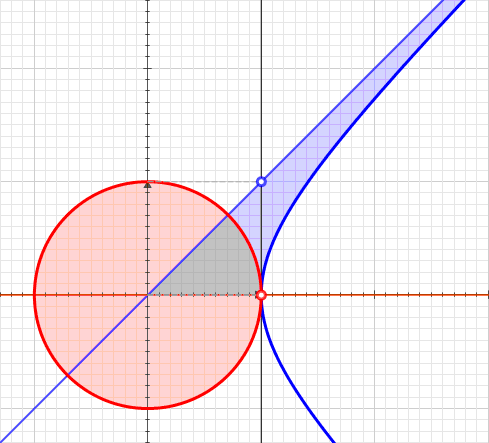
Hyperbolic Sector
A hyperbolic sector is a region of the Cartesian plane bounded by a hyperbola and two rays from the origin to it. For example, the two points and on the rectangular hyperbola , or the corresponding region when this hyperbola is re-scaled and its orientation is altered by a rotation leaving the center at the origin, as with the unit hyperbola. A hyperbolic sector in standard position has and . Hyperbolic sectors are the basis for the hyperbolic functions. Area The area of a hyperbolic sector in standard position is natural logarithm of ''b'' . Proof: Integrate under 1/''x'' from 1 to ''b'', add triangle , and subtract triangle . When in standard position, a hyperbolic sector corresponds to a positive hyperbolic angle at the origin, with the measure of the latter being defined as the area of the former. Hyperbolic triangle When in standard position, a hyperbolic sector determines a hyperbolic triangle, the right triangle with one vertex at the origin, base on the diag ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Area
Area is the quantity that expresses the extent of a region on the plane or on a curved surface. The area of a plane region or ''plane area'' refers to the area of a shape A shape or figure is a graphics, graphical representation of an object or its external boundary, outline, or external Surface (mathematics), surface, as opposed to other properties such as color, Surface texture, texture, or material type. A pl ... or planar lamina, while ''surface area'' refers to the area of an open surface or the boundary (mathematics), boundary of a solid geometry, three-dimensional object. Area can be understood as the amount of material with a given thickness that would be necessary to fashion a model of the shape, or the amount of paint necessary to cover the surface with a single coat. It is the two-dimensional analogue of the length of a plane curve, curve (a one-dimensional concept) or the volume of a solid (a three-dimensional concept). The area of a shape can be measured by com ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Hyperbolic Angle
In geometry, hyperbolic angle is a real number determined by the area of the corresponding hyperbolic sector of ''xy'' = 1 in Quadrant I of the Cartesian plane. The hyperbolic angle parametrises the unit hyperbola, which has hyperbolic functions as coordinates. In mathematics, hyperbolic angle is an invariant measure as it is preserved under hyperbolic rotation. The hyperbola ''xy'' = 1 is rectangular with a semi-major axis of \sqrt 2, analogous to the magnitude of a circular angle corresponding to the area of a circular sector in a circle with radius \sqrt 2. Hyperbolic angle is used as the independent variable for the hyperbolic functions sinh, cosh, and tanh, because these functions may be premised on hyperbolic analogies to the corresponding circular trigonometric functions by regarding a hyperbolic angle as defining a hyperbolic triangle. The parameter thus becomes one of the most useful in the calculus of real variables. Definition Consider the rectangular hyperbola \text ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Affine Geometry
In mathematics, affine geometry is what remains of Euclidean geometry when ignoring (mathematicians often say "forgetting") the metric notions of distance and angle. As the notion of ''parallel lines'' is one of the main properties that is independent of any metric, affine geometry is often considered as the study of parallel lines. Therefore, Playfair's axiom (Given a line L and a point P not on L, there is exactly one line parallel to L that passes through P.) is fundamental in affine geometry. Comparisons of figures in affine geometry are made with affine transformations, which are mappings that preserve alignment of points and parallelism of lines. Affine geometry can be developed in two ways that are essentially equivalent. In synthetic geometry, an affine space is a set of ''points'' to which is associated a set of lines, which satisfy some axioms (such as Playfair's axiom). Affine geometry can also be developed on the basis of linear algebra. In this context an affine s ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Russian Language
Russian (russian: русский язык, russkij jazyk, link=no, ) is an East Slavic languages, East Slavic language mainly spoken in Russia. It is the First language, native language of the Russians, and belongs to the Indo-European languages, Indo-European language family. It is one of four living East Slavic languages, and is also a part of the larger Balto-Slavic languages. Besides Russia itself, Russian is an official language in Belarus, Kazakhstan, and Kyrgyzstan, and is used widely as a lingua franca throughout Ukraine, the Caucasus, Central Asia, and to some extent in the Baltic states. It was the De facto#National languages, ''de facto'' language of the former Soviet Union,1977 Soviet Constitution, Constitution and Fundamental Law of the Union of Soviet Socialist Republics, 1977: Section II, Chapter 6, Article 36 and continues to be used in public life with varying proficiency in all of the post-Soviet states. Russian has over 258 million total speakers worldwide. ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Ural State University
The Ural State University (russian: Урáльский госудáрственный университéт и́мени А.М. Гóрького, , often shortened to USU, УрГУ) is a public university located in the city of Yekaterinburg, Sverdlovsk Oblast, Russian Federation. Founded in 1920, it was an exclusive educational establishment made of several institutes (educational and scientific divisions) which later became independent universities and schools. Established in 1936 the university was named after one of its founders, Russian author Maxim Gorky. It is the second oldest University in the Middle Urals (the oldest being Urals State University of Mines) and one of the most prestigious universities in Russia; preparing research, educational and managerial elite on the basis of the integration of academic process and scientific research. It offers education in dozens of scientific and educational fields including 53 graduate programs. In 2007 Dmitriy Bugrov was electe ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Ural Mountains
The Ural Mountains ( ; rus, Ура́льские го́ры, r=Uralskiye gory, p=ʊˈralʲskʲɪjə ˈɡorɨ; ba, Урал тауҙары) or simply the Urals, are a mountain range that runs approximately from north to south through western Russia, from the coast of the Arctic Ocean to the river Ural and northwestern Kazakhstan.Ural Mountains Encyclopædia Britannica on-line The mountain range forms part of the conventional boundary between the regions of and |
