|
Inverse Iteration
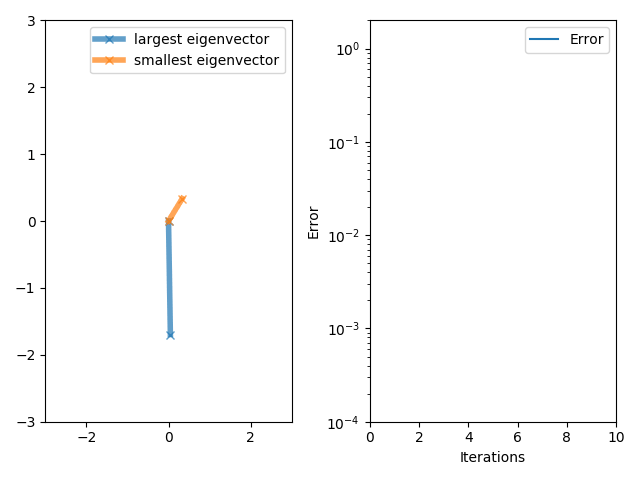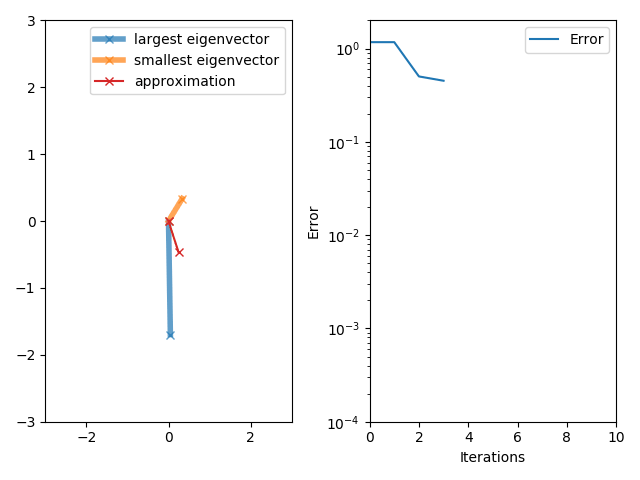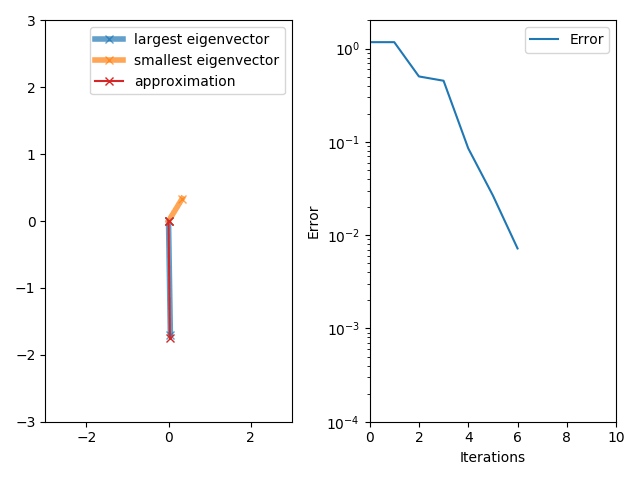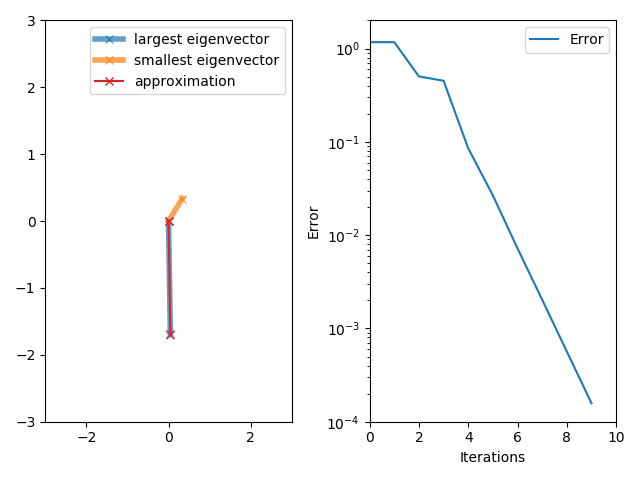
In numerical analysis, inverse iteration (also known as the ''inverse power method'') is an iterative eigenvalue algorithm. It allows one to find an approximate eigenvector when an approximation to a corresponding eigenvalue is already known. The method is conceptually similar to the power method. It appears to have originally been developed to compute resonance frequencies in the field of structural mechanics. Ernst Pohlhausen, ''Berechnung der Eigenschwingungen statisch-bestimmter Fachwerke'', ZAMM - Zeitschrift für Angewandte Mathematik und Mechanik 1, 28-42 (1921). The inverse power iteration algorithm starts with an approximation \mu for the eigenvalue corresponding to the desired eigenvector and a vector b_0, either a randomly selected vector or an approximation to the eigenvector. The method is described by the iteration : b_ = \frac, where C_k are some constants usually chosen as C_k= \, (A - \mu I)^b_k \, . Since eigenvectors are defined up to multiplication by constan ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Numerical Analysis
Numerical analysis is the study of algorithms that use numerical approximation (as opposed to symbolic computation, symbolic manipulations) for the problems of mathematical analysis (as distinguished from discrete mathematics). It is the study of numerical methods that attempt at finding approximate solutions of problems rather than the exact ones. Numerical analysis finds application in all fields of engineering and the physical sciences, and in the 21st century also the life and social sciences, medicine, business and even the arts. Current growth in computing power has enabled the use of more complex numerical analysis, providing detailed and realistic mathematical models in science and engineering. Examples of numerical analysis include: ordinary differential equations as found in celestial mechanics (predicting the motions of planets, stars and galaxies), numerical linear algebra in data analysis, and stochastic differential equations and Markov chains for simulating living ce ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Society For Industrial And Applied Mathematics
Society for Industrial and Applied Mathematics (SIAM) is a professional society dedicated to applied mathematics, computational science, and data science through research, publications, and community. SIAM is the world's largest scientific society devoted to applied mathematics, and roughly two-thirds of its membership resides within the United States. Founded in 1951, the organization began holding annual national meetings in 1954, and now hosts conferences, publishes books and scholarly journals, and engages in advocacy in issues of interest to its membership. Members include engineers, scientists, and mathematicians, both those employed in academia and those working in industry. The society supports educational institutions promoting applied mathematics. SIAM is one of the four member organizations of the Joint Policy Board for Mathematics. Membership Membership is open to both individuals and organizations. By the end of its first full year of operation, SIAM had 130 memb ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Power Iteration
In mathematics, power iteration (also known as the power method) is an eigenvalue algorithm: given a diagonalizable matrix (mathematics), matrix A, the algorithm will produce a number \lambda, which is the greatest (in absolute value) eigenvalue of A, and a nonzero vector v, which is a corresponding eigenvector of \lambda, that is, Av = \lambda v. The algorithm is also known as the Von Mises iteration.Richard von Mises and H. Pollaczek-Geiringer, ''Praktische Verfahren der Gleichungsauflösung'', ZAMM - Zeitschrift für Angewandte Mathematik und Mechanik 9, 152-164 (1929). Power iteration is a very simple algorithm, but it may converge slowly. The most time-consuming operation of the algorithm is the multiplication of matrix A by a vector, so it is effective for a very large sparse matrix with appropriate implementation. The method The power iteration algorithm starts with a vector b_0, which may be an approximation to the dominant eigenvector or a random vector. The method is de ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Matrix Norm
In mathematics, a matrix norm is a vector norm in a vector space whose elements (vectors) are matrices (of given dimensions). Preliminaries Given a field K of either real or complex numbers, let K^ be the -vector space of matrices with m rows and n columns and entries in the field K. A matrix norm is a norm on K^. This article will always write such norms with double vertical bars (like so: \, A\, ). Thus, the matrix norm is a function \, \cdot\, : K^ \to \R that must satisfy the following properties: For all scalars \alpha \in K and matrices A, B \in K^, *\, A\, \ge 0 (''positive-valued'') *\, A\, = 0 \iff A=0_ (''definite'') *\left\, \alpha A\right\, =\left, \alpha\ \left\, A\right\, (''absolutely homogeneous'') *\, A+B\, \le \, A\, +\, B\, (''sub-additive'' or satisfying the ''triangle inequality'') The only feature distinguishing matrices from rearranged vectors is multiplication. Matrix norms are particularly useful if they are also sub-multiplicative: *\left\, ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Rayleigh Quotient
In mathematics, the Rayleigh quotient () for a given complex Hermitian matrix ''M'' and nonzero vector ''x'' is defined as: R(M,x) = . For real matrices and vectors, the condition of being Hermitian reduces to that of being symmetric, and the conjugate transpose x^ to the usual transpose x'. Note that R(M, c x) = R(M,x) for any non-zero scalar ''c''. Recall that a Hermitian (or real symmetric) matrix is diagonalizable with only real eigenvalues. It can be shown that, for a given matrix, the Rayleigh quotient reaches its minimum value \lambda_\min (the smallest eigenvalue of ''M'') when ''x'' is v_\min (the corresponding eigenvector). Similarly, R(M, x) \leq \lambda_\max and R(M, v_\max) = \lambda_\max. The Rayleigh quotient is used in the min-max theorem to get exact values of all eigenvalues. It is also used in eigenvalue algorithms (such as Rayleigh quotient iteration) to obtain an eigenvalue approximation from an eigenvector approximation. The range of the Rayleigh quotient ( ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Rayleigh Quotient Iteration
Rayleigh quotient iteration is an eigenvalue algorithm which extends the idea of the inverse iteration by using the Rayleigh quotient to obtain increasingly accurate eigenvalue estimates. Rayleigh quotient iteration is an iterative method, that is, it delivers a sequence of approximate solutions that converges to a true solution in the limit. Very rapid convergence is guaranteed and no more than a few iterations are needed in practice to obtain a reasonable approximation. The Rayleigh quotient iteration algorithm converges cubically for Hermitian or symmetric matrices, given an initial vector that is sufficiently close to an eigenvector of the matrix that is being analyzed. Algorithm The algorithm is very similar to inverse iteration, but replaces the estimated eigenvalue at the end of each iteration with the Rayleigh quotient. Begin by choosing some value \mu_0 as an initial eigenvalue guess for the Hermitian matrix A. An initial vector b_0 must also be supplied as init ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Bisection Eigenvalue Algorithm
In geometry, bisection is the division of something into two equal or congruent parts, usually by a line, which is then called a ''bisector''. The most often considered types of bisectors are the ''segment bisector'' (a line that passes through the midpoint of a given segment) and the ''angle bisector'' (a line that passes through the apex of an angle, that divides it into two equal angles). In three-dimensional space, bisection is usually done by a plane, also called the ''bisector'' or ''bisecting plane''. Perpendicular line segment bisector Definition *The perpendicular bisector of a line segment is a line, which meets the segment at its midpoint perpendicularly. The Horizontal intersector of a segment AB also has the property that each of its points X is equidistant from the segment's endpoints: (D)\quad , XA, = , XB, . The proof follows from and Pythagoras' theorem: :, XA, ^2=, XM, ^2+, MA, ^2=, XM, ^2+, MB, ^2=, XB, ^2 \; . Property (D) is usually used for t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Integer Overflow
In computer programming, an integer overflow occurs when an arithmetic operation attempts to create a numeric value that is outside of the range that can be represented with a given number of digits – either higher than the maximum or lower than the minimum representable value. The most common result of an overflow is that the least significant representable digits of the result are stored; the result is said to ''wrap'' around the maximum (i.e. modulo a power of the radix, usually two in modern computers, but sometimes ten or another radix). An overflow condition may give results leading to unintended behavior. In particular, if the possibility has not been anticipated, overflow can compromise a program's reliability and security. For some applications, such as timers and clocks, wrapping on overflow can be desirable. The C11 standard states that for unsigned integers, modulo wrapping is the defined behavior and the term overflow never applies: "a computation involving un ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Floating Point
In computing, floating-point arithmetic (FP) is arithmetic that represents real numbers approximately, using an integer with a fixed precision, called the significand, scaled by an integer exponent of a fixed base. For example, 12.345 can be represented as a base-ten floating-point number: 12.345 = \underbrace_\text \times \underbrace_\text\!\!\!\!\!\!^ In practice, most floating-point systems use base two, though base ten (decimal floating point) is also common. The term ''floating point'' refers to the fact that the number's radix point can "float" anywhere to the left, right, or between the significant digits of the number. This position is indicated by the exponent, so floating point can be considered a form of scientific notation. A floating-point system can be used to represent, with a fixed number of digits, numbers of very different orders of magnitude — such as the number of meters between galaxies or between protons in an atom. For this reason, floating-poin ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Fixed-point Arithmetic
In computing, fixed-point is a method of representing fractional (non-integer) numbers by storing a fixed number of digits of their fractional part. Dollar amounts, for example, are often stored with exactly two fractional digits, representing the cents (1/100 of dollar). More generally, the term may refer to representing fractional values as integer multiples of some fixed small unit, e.g. a fractional amount of hours as an integer multiple of ten-minute intervals. Fixed-point number representation is often contrasted to the more complicated and computationally demanding floating-point representation. In the fixed-point representation, the fraction is often expressed in the same number base as the integer part, but using negative powers of the base ''b''. The most common variants are decimal (base 10) and binary (base 2). The latter is commonly known also as binary scaling. Thus, if ''n'' fraction digits are stored, the value will always be an integer multiple of ''b' ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Bitwise Operation
In computer programming, a bitwise operation operates on a bit string, a bit array or a binary numeral (considered as a bit string) at the level of its individual bits. It is a fast and simple action, basic to the higher-level arithmetic operations and directly supported by the processor. Most bitwise operations are presented as two-operand instructions where the result replaces one of the input operands. On simple low-cost processors, typically, bitwise operations are substantially faster than division, several times faster than multiplication, and sometimes significantly faster than addition. While modern processors usually perform addition and multiplication just as fast as bitwise operations due to their longer instruction pipelines and other architectural design choices, bitwise operations do commonly use less power because of the reduced use of resources. Bitwise operators In the explanations below, any indication of a bit's position is counted from the right (least signi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Application-specific Integrated Circuit
An application-specific integrated circuit (ASIC ) is an integrated circuit (IC) chip customized for a particular use, rather than intended for general-purpose use, such as a chip designed to run in a digital voice recorder or a high-efficiency video codec. Application-specific standard product (ASSP) chips are intermediate between ASICs and industry standard integrated circuits like the 7400 series or the 4000 series. ASIC chips are typically fabricated using metal-oxide-semiconductor (MOS) technology, as MOS integrated circuit chips. As feature sizes have shrunk and design tools improved over the years, the maximum complexity (and hence functionality) possible in an ASIC has grown from 5,000 logic gates to over 100 million. Modern ASICs often include entire microprocessors, memory blocks including ROM, RAM, EEPROM, flash memory and other large building blocks. Such an ASIC is often termed a SoC (system-on-chip). Designers of digital ASICs often use a hardware descrip ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
