|
Interaction Effects
In statistics, an interaction may arise when considering the relationship among three or more variables, and describes a situation in which the effect of one causal variable on an outcome depends on the state of a second causal variable (that is, when effects of the two causes are not additive). Although commonly thought of in terms of causal relationships, the concept of an interaction can also describe non-causal associations (then also called moderation or effect modification). Interactions are often considered in the context of regression analyses or factorial experiments. The presence of interactions can have important implications for the interpretation of statistical models. If two variables of interest interact, the relationship between each of the interacting variables and a third "dependent variable" depends on the value of the other interacting variable. In practice, this makes it more difficult to predict the consequences of changing the value of a variable, parti ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
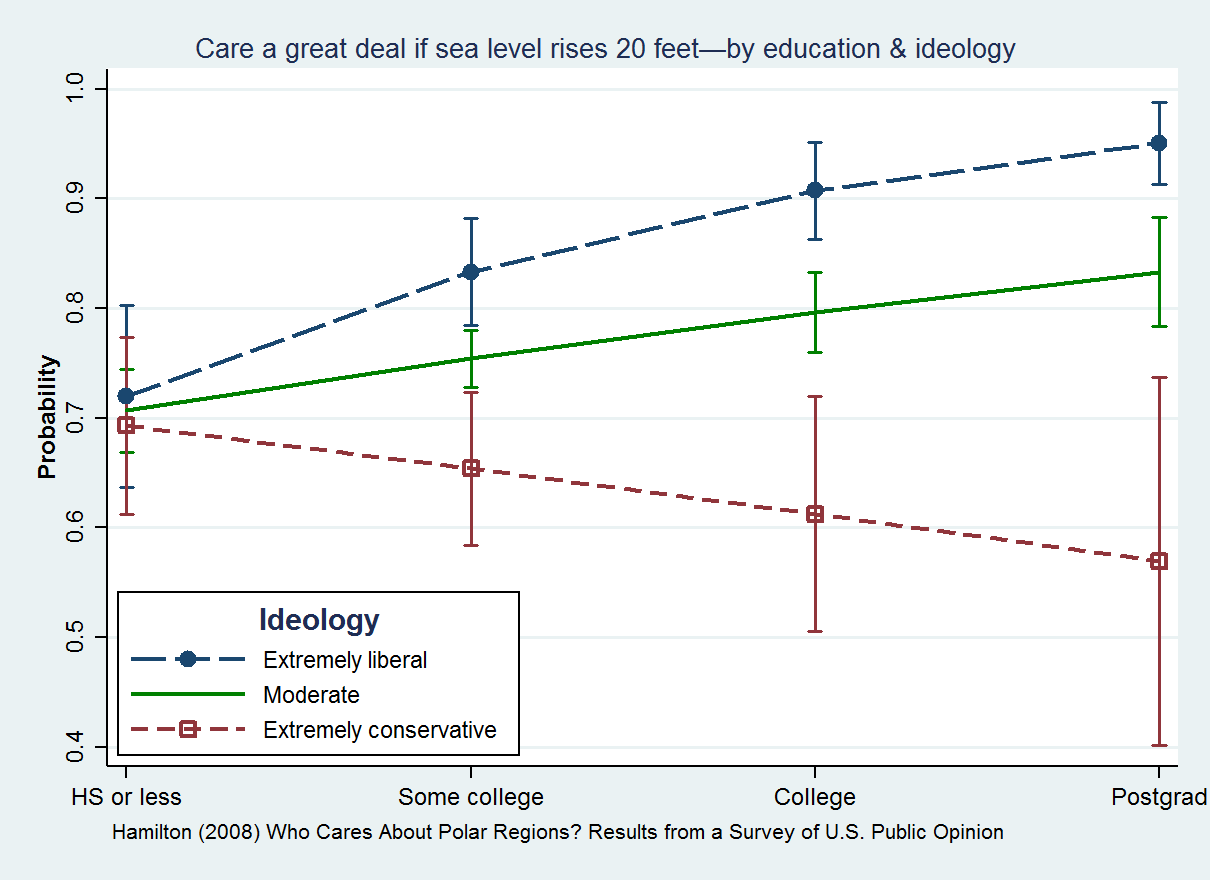
GSS Sealevel Interaction
GSS may refer to: Education * Garibaldi Secondary School, in Maple Ridge, British Columbia, Canada * The Gifted Students' School (Iraq), in Baghdad * Government Secondary School (other) * Greenridge Secondary School, in Singapore * Grimsby Secondary School, in Ontario, Canada * GSS Institute of Technology, in Bangalore, India * Gay Student Services, now GLBT Aggies, at Texas A&M University Government and politics * Global Standards Symposium * Civic Alliance of Serbia (Serbian: '), a political party in Serbia * Government Statistical Service, of the Government of the United Kingdom * Israeli General Security Service, also known as ''Shin Bet'' * Ghana Statistical Service, of the Government of Ghana Science * General Social Survey * Genome survey sequence * Gerstmann–Sträussler–Scheinker syndrome * Glutathione synthetase * Granulomatous slack skin * Gudjonsson suggestibility scale Sport * Grønlands Seminarius Sportklub, a Greenlandic sport club * Gurpre ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Genichi Taguchi
was an engineer and statistician. From the 1950s onwards, Taguchi developed a methodology for applying statistics to improve the quality of manufactured goods. Taguchi methods have been controversial among some conventional Western statisticians, but others have accepted many of the concepts introduced by him as valid extensions to the body of knowledge. Biography Taguchi was born and raised in the textile town of Tokamachi, in Niigata prefecture. He initially studied textile engineering at Kiryu Technical College with the intention of entering the family kimono business. However, with the escalation of World War II in 1942, he was drafted into the Astronomical Department of the Navigation Institute of the Imperial Japanese Navy. After the war, in 1948 he joined the Ministry of Public Health and Welfare, where he came under the influence of eminent statistician Matosaburo Masuyama, who kindled his interest in the design of experiments. He also worked at the Institute of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Body Temperature Species Data 2
Body may refer to: In science * Physical body, an object in physics that represents a large amount, has mass or takes up space * Body (biology), the physical material of an organism * Body plan, the physical features shared by a group of animals * Human body, the entire structure of a human organism ** Dead body, cadaver, or corpse, a dead human body * (living) matter, see: Mind–body problem, the relationship between mind and matter in philosophy * Aggregates within living matter, such as inclusion bodies In arts and entertainment In film and television * ''Body'' (2015 Polish film), a 2015 Polish film * ''Body'' (2015 American film), a 2015 American film * "Body" (''Wonder Showzen'' episode), a 2006 episode of American sketch comedy television series ''Wonder Showzen'' * "Body", an episode of the Adult Swim television series, '' Off the Air'' In literature and publishing * body text, the text forming the main content of any printed matter * body (typography), the size of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Logit Regression
In statistics, the logistic model (or logit model) is a statistical model that models the probability of an event taking place by having the log-odds for the event be a linear combination of one or more independent variables. In regression analysis, logistic regression (or logit regression) is estimating the parameters of a logistic model (the coefficients in the linear combination). Formally, in binary logistic regression there is a single binary dependent variable, coded by an indicator variable, where the two values are labeled "0" and "1", while the independent variables can each be a binary variable (two classes, coded by an indicator variable) or a continuous variable (any real value). The corresponding probability of the value labeled "1" can vary between 0 (certainly the value "0") and 1 (certainly the value "1"), hence the labeling; the function that converts log-odds to probability is the logistic function, hence the name. The unit of measurement for the log-odds scale ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Generalized Linear Model
In statistics, a generalized linear model (GLM) is a flexible generalization of ordinary linear regression. The GLM generalizes linear regression by allowing the linear model to be related to the response variable via a ''link function'' and by allowing the magnitude of the variance of each measurement to be a function of its predicted value. Generalized linear models were formulated by John Nelder and Robert Wedderburn as a way of unifying various other statistical models, including linear regression, logistic regression and Poisson regression. They proposed an iteratively reweighted least squares method for maximum likelihood estimation (MLE) of the model parameters. MLE remains popular and is the default method on many statistical computing packages. Other approaches, including Bayesian regression and least squares fitting to variance stabilized responses, have been developed. Intuition Ordinary linear regression predicts the expected value of a given unknown quantity ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Multilevel Model
Multilevel models (also known as hierarchical linear models, linear mixed-effect model, mixed models, nested data models, random coefficient, random-effects models, random parameter models, or split-plot designs) are statistical models of parameters that vary at more than one level. An example could be a model of student performance that contains measures for individual students as well as measures for classrooms within which the students are grouped. These models can be seen as generalizations of linear models (in particular, linear regression), although they can also extend to non-linear models. These models became much more popular after sufficient computing power and software became available. Multilevel models are particularly appropriate for research designs where data for participants are organized at more than one level (i.e., nested data). The units of analysis are usually individuals (at a lower level) who are nested within contextual/aggregate units (at a higher level ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Quantile Regression
Quantile regression is a type of regression analysis used in statistics and econometrics. Whereas the method of least squares estimates the conditional ''mean'' of the response variable across values of the predictor variables, quantile regression estimates the conditional '' median'' (or other ''quantiles'') of the response variable. Quantile regression is an extension of linear regression used when the conditions of linear regression are not met. Advantages and applications One advantage of quantile regression relative to ordinary least squares regression is that the quantile regression estimates are more robust against outliers in the response measurements. However, the main attraction of quantile regression goes beyond this and is advantageous when conditional quantile functions are of interest. Different measures of central tendency and statistical dispersion can be useful to obtain a more comprehensive analysis of the relationship between variables. In ecology, quantil ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Robust Regression
In robust statistics, robust regression seeks to overcome some limitations of traditional regression analysis. A regression analysis models the relationship between one or more independent variables and a dependent variable. Standard types of regression, such as ordinary least squares, have favourable properties if their underlying assumptions are true, but can give misleading results otherwise (i.e. are not robust to assumption violations). Robust regression methods are designed to limit the effect that violations of assumptions by the underlying data-generating process have on regression estimates. For example, least squares estimates for regression models are highly sensitive to outliers: an outlier with twice the error magnitude of a typical observation contributes four (two squared) times as much to the squared error loss, and therefore has more leverage over the regression estimates. The Huber loss function is a robust alternative to standard square error loss that redu ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Ordinary Least Squares
In statistics, ordinary least squares (OLS) is a type of linear least squares method for choosing the unknown parameters in a linear regression model (with fixed level-one effects of a linear function of a set of explanatory variables) by the principle of least squares: minimizing the sum of the squares of the differences between the observed dependent variable (values of the variable being observed) in the input dataset and the output of the (linear) function of the independent variable. Geometrically, this is seen as the sum of the squared distances, parallel to the axis of the dependent variable, between each data point in the set and the corresponding point on the regression surface—the smaller the differences, the better the model fits the data. The resulting estimator can be expressed by a simple formula, especially in the case of a simple linear regression, in which there is a single regressor on the right side of the regression equation. The OLS estimator is con ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Tea Party Interaction
Tea is an aromatic beverage prepared by pouring hot or boiling water over cured or fresh leaves of ''Camellia sinensis'', an evergreen shrub native to East Asia which probably originated in the borderlands of southwestern China and northern Myanmar. Tea is also rarely made from the leaves of ''Camellia taliensis''. After plain water, tea is the most widely consumed drink in the world. There are many different types of tea; some have a cooling, slightly bitter, and astringent flavour, while others have vastly different profiles that include sweet, nutty, floral, or grassy notes. Tea has a stimulating effect in humans primarily due to its caffeine content. An early credible record of tea drinking dates to the third century AD, in a medical text written by Chinese physician Hua Tuo. It was popularised as a recreational drink during the Chinese Tang dynasty, and tea drinking subsequently spread to other East Asian countries. Portuguese priests and merchants introduced it to ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Multicollinearity
In statistics, multicollinearity (also collinearity) is a phenomenon in which one predictor variable in a multiple regression model can be linearly predicted from the others with a substantial degree of accuracy. In this situation, the coefficient estimates of the multiple regression may change erratically in response to small changes in the model or the data. Multicollinearity does not reduce the predictive power or reliability of the model as a whole, at least within the sample data set; it only affects calculations regarding individual predictors. That is, a multivariate regression model with collinear predictors can indicate how well the entire bundle of predictors predicts the outcome variable, but it may not give valid results about any individual predictor, or about which predictors are redundant with respect to others. Note that in statements of the assumptions underlying regression analyses such as ordinary least squares, the phrase "no multicollinearity" usually refe ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Dummy Variable (statistics)
In regression analysis, a dummy variable (also known as indicator variable or just dummy) is one that takes the values 0 or 1 to indicate the absence or presence of some categorical effect that may be expected to shift the outcome. For example, if we were studying the relationship between gender and income, we could use a dummy variable to represent the gender of each individual in the study. The variable would take on a value of 1 for males and 0 for females. Dummy variables are commonly used in regression analysis to represent categorical variables that have more than two levels, such as education level or occupation. In this case, multiple dummy variables would be created to represent each level of the variable, and only one dummy variable would take on a value of 1 for each observation. Dummy variables are useful because they allow us to include categorical variables in our analysis, which would otherwise be difficult to include due to their non-numeric nature. They can also h ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |