|
Integrally-convex Set
An integrally convex set is the discrete geometry analogue of the concept of convex set in geometry. A subset ''X'' of the integer grid \mathbb^n is integrally convex if any point ''y'' in the convex hull of ''X'' can be expressed as a convex combination In convex geometry and vector algebra, a convex combination is a linear combination of points (which can be vectors, scalars, or more generally points in an affine space) where all coefficients are non-negative and sum to 1. In other w ... of the points of ''X'' that are "near" ''y'', where "near" means that the distance between each two coordinates is less than 1. Definitions Let ''X'' be a subset of \mathbb^n. Denote by ch(''X'') the convex hull of ''X''. Note that ch(''X'') is a subset of \mathbb^n, since it contains all the real points that are convex combinations of the integer points in ''X''. For any point ''y'' in \mathbb^n, denote near(''y'') := . These are the integer points that are considered "near ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Discrete Geometry
Discrete geometry and combinatorial geometry are branches of geometry that study combinatorial properties and constructive methods of discrete geometric objects. Most questions in discrete geometry involve finite or discrete sets of basic geometric objects, such as points, lines, planes, circles, spheres, polygons, and so forth. The subject focuses on the combinatorial properties of these objects, such as how they intersect one another, or how they may be arranged to cover a larger object. Discrete geometry has a large overlap with convex geometry and computational geometry, and is closely related to subjects such as finite geometry, combinatorial optimization, digital geometry, discrete differential geometry, geometric graph theory, toric geometry, and combinatorial topology. History Although polyhedra and tessellations had been studied for many years by people such as Kepler and Cauchy, modern discrete geometry has its origins in the late 19th century. Early topics studie ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Convex Set
In geometry, a subset of a Euclidean space, or more generally an affine space over the reals, is convex if, given any two points in the subset, the subset contains the whole line segment that joins them. Equivalently, a convex set or a convex region is a subset that intersects every line into a single line segment (possibly empty). For example, a solid cube is a convex set, but anything that is hollow or has an indent, for example, a crescent shape, is not convex. The boundary of a convex set is always a convex curve. The intersection of all the convex sets that contain a given subset of Euclidean space is called the convex hull of . It is the smallest convex set containing . A convex function is a real-valued function defined on an interval with the property that its epigraph (the set of points on or above the graph of the function) is a convex set. Convex minimization is a subfield of optimization that studies the problem of minimizing convex functions over convex se ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Convex Hull
In geometry, the convex hull or convex envelope or convex closure of a shape is the smallest convex set that contains it. The convex hull may be defined either as the intersection of all convex sets containing a given subset of a Euclidean space, or equivalently as the set of all convex combinations of points in the subset. For a bounded subset of the plane, the convex hull may be visualized as the shape enclosed by a rubber band stretched around the subset. Convex hulls of open sets are open, and convex hulls of compact sets are compact. Every compact convex set is the convex hull of its extreme points. The convex hull operator is an example of a closure operator, and every antimatroid can be represented by applying this closure operator to finite sets of points. The algorithmic problems of finding the convex hull of a finite set of points in the plane or other low-dimensional Euclidean spaces, and its dual problem of intersecting half-spaces, are fundamental problems of com ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
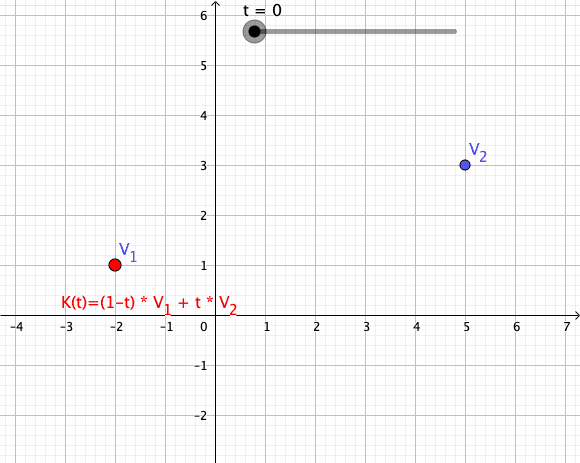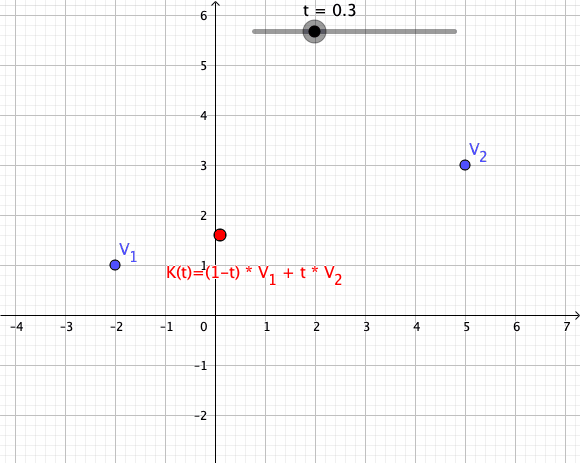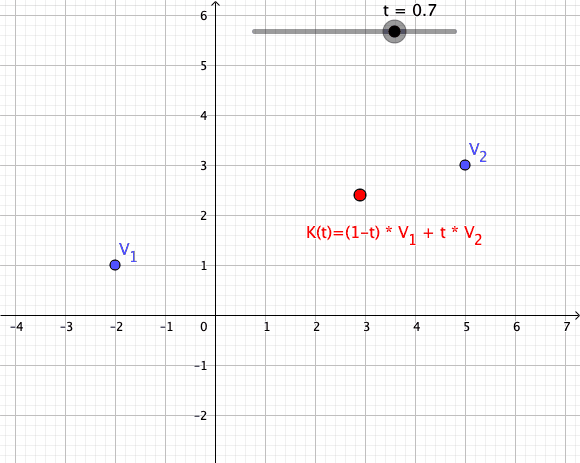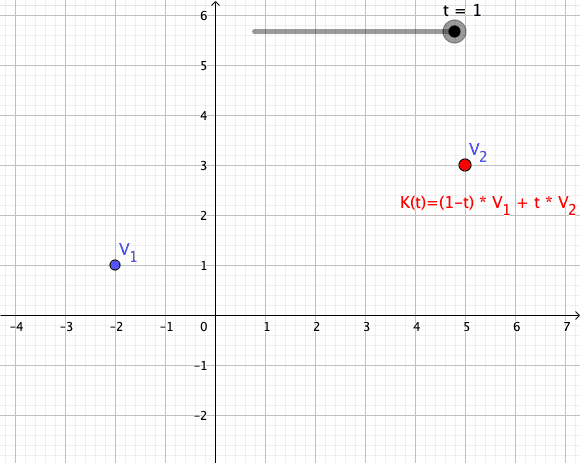
Convex Combination
In convex geometry and vector algebra, a convex combination is a linear combination of points (which can be vectors, scalars, or more generally points in an affine space) where all coefficients are non-negative and sum to 1. In other words, the operation is equivalent to a standard weighted average, but whose weights are expressed as a percent of the total weight, instead of as a fraction of the ''count'' of the weights as in a standard weighted average. More formally, given a finite number of points x_1, x_2, \dots, x_n in a real vector space, a convex combination of these points is a point of the form :\alpha_1x_1+\alpha_2x_2+\cdots+\alpha_nx_n where the real numbers \alpha_i satisfy \alpha_i\ge 0 and \alpha_1+\alpha_2+\cdots+\alpha_n=1. As a particular example, every convex combination of two points lies on the line segment between the points. A set is convex if it contains all convex combinations of its points. The convex hull of a given set of points is identical ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Triangulation (topology)
In mathematics, triangulation describes the replacement of topological spaces by piecewise linear spaces, i.e. the choice of a homeomorphism in a suitable simplicial complex. Spaces being homeomorphic to a simplicial complex are called triangulable. Triangulation has various uses in different branches of mathematics, for instance in algebraic topology, in complex analysis or in modeling. Motivation On the one hand, it is sometimes useful to forget about superfluous information of topological spaces: The replacement of the original spaces with simplicial complexes may help to recognize crucial properties and to gain a better understanding of the considered object. On the other hand, simplicial complexes are objects of combinatorial character and therefore one can assign them quantities rising from their combinatorial pattern, for instance, the Euler characteristic. Triangulation allows now to assign such quantities to topological spaces. Investigations concerning the exist ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |