|
Implied Volatility Surface
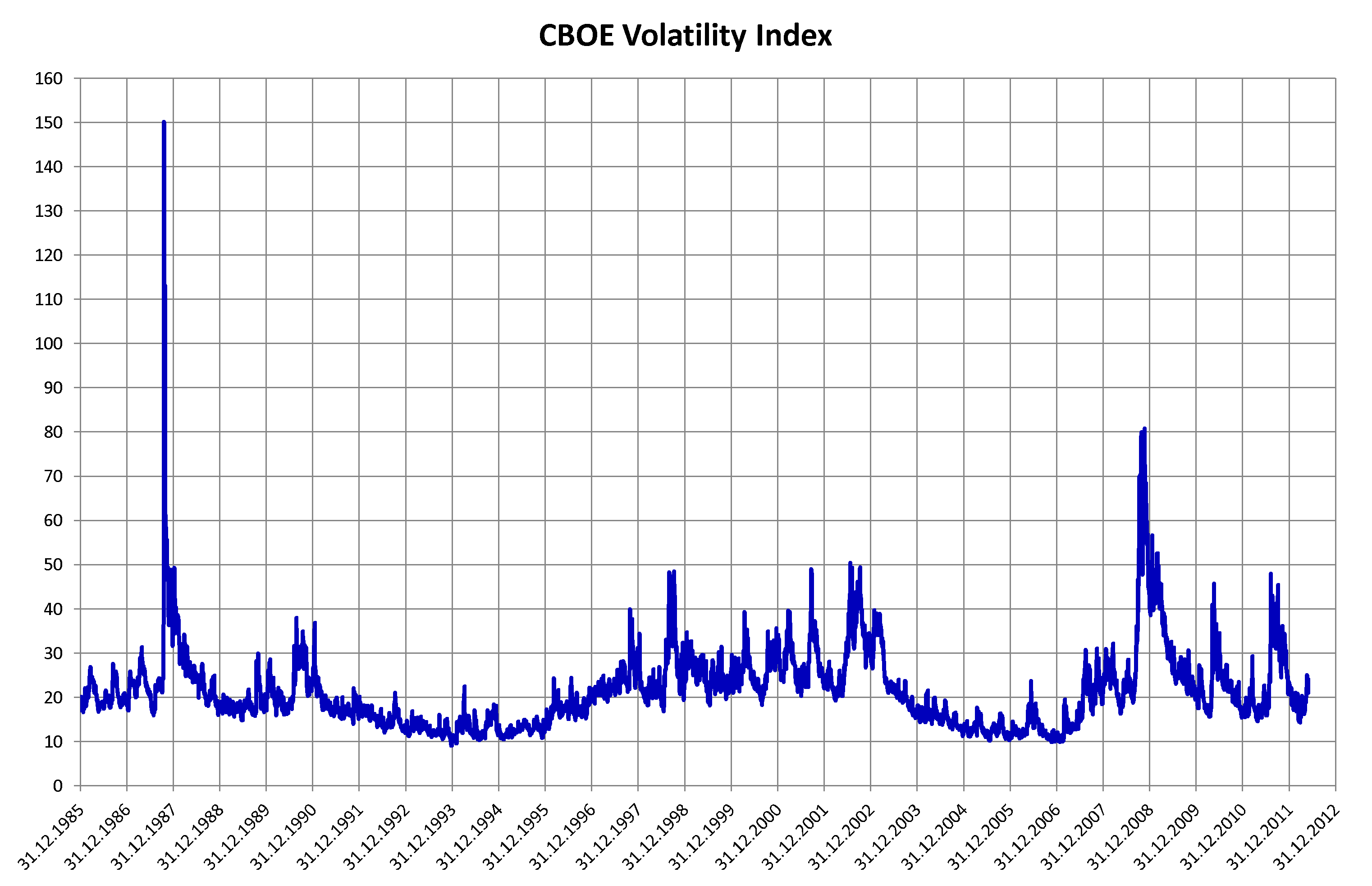
Volatility smiles are implied volatility patterns that arise in pricing financial options. It is a parameter (implied volatility) that is needed to be modified for the Black–Scholes formula to fit market prices. In particular for a given expiration, options whose strike price differs substantially from the underlying asset's price command higher prices (and thus implied volatilities) than what is suggested by standard option pricing models. These options are said to be either deep in-the-money or out-of-the-money. Graphing implied volatilities against strike prices for a given expiry produces a skewed "smile" instead of the expected flat surface. The pattern differs across various markets. Equity options traded in American markets did not show a volatility smile before the Crash of 1987 but began showing one afterwards. It is believed that investor reassessments of the probabilities of fat-tail have led to higher prices for out-of-the-money options. This anomaly implies de ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Volatility Smile
Volatility smiles are implied volatility patterns that arise in pricing financial options. It is a parameter (implied volatility) that is needed to be modified for the Black–Scholes formula to fit market prices. In particular for a given expiration, options whose strike price differs substantially from the underlying asset's price command higher prices (and thus implied volatilities) than what is suggested by standard option pricing models. These options are said to be either deep in-the-money or out-of-the-money. Graphing implied volatilities against strike prices for a given expiry produces a skewed "smile" instead of the expected flat surface. The pattern differs across various markets. Equity options traded in American markets did not show a volatility smile before the Crash of 1987 but began showing one afterwards. It is believed that investor reassessments of the probabilities of fat-tail have led to higher prices for out-of-the-money options. This anomaly implies de ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Root Finding Algorithm
In mathematics and computing, a root-finding algorithm is an algorithm for finding zeros, also called "roots", of continuous functions. A zero of a function , from the real numbers to real numbers or from the complex numbers to the complex numbers, is a number such that . As, generally, the zeros of a function cannot be computed exactly nor expressed in closed form, root-finding algorithms provide approximations to zeros, expressed either as floating-point numbers or as small isolating intervals, or disks for complex roots (an interval or disk output being equivalent to an approximate output together with an error bound). Solving an equation is the same as finding the roots of the function . Thus root-finding algorithms allow solving any equation defined by continuous functions. However, most root-finding algorithms do not guarantee that they will find all the roots; in particular, if such an algorithm does not find any root, that does not mean that no root exists. Most ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Vanna Volga
Vanna () is a given name that first appeared in recorded European history circa 1294. The Italian medieval feminine name originated in Tuscany, and is particular to Florence, Italy. Though similar in pronunciation to the Italian name Giovanna, and conjectured to be derived from it, Vanna is neither a nickname nor a derivation. History The name Vanna first appears in print in ''La Vita Nuova'', a 1294 book of verse written by Dante Alighieri, an Italian Florentine poet. In one verse, Dante writes that (anthropomorphized) Love itself proclaims that Vanna is ''Primavera'' ("Springtime") and declares that Beatrice's name is "Love". Vanna is also a Cambodian unisex name ( ) meaning "Gold". It originates from ancient Sanskrit . Cambodian names are chosen for various themes such as Nature and positive attributes. Variations Vannetta; Vanetta; Vannina; Vanni, similar to the first name Ivanna. Meanings and usage The name Vanna is particular to the Tuscan province of Italy ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
SABR Volatility Model
In mathematical finance, the SABR model is a stochastic volatility model, which attempts to capture the volatility smile in derivatives markets. The name stands for "stochastic alpha, beta, rho", referring to the parameters of the model. The SABR model is widely used by practitioners in the financial industry, especially in the interest rate derivative markets. It was developed by Patrick S. Hagan, Deep Kumar, Andrew Lesniewski, and Diana Woodward. Dynamics The SABR model describes a single forward F, such as a LIBOR forward rate, a forward swap rate, or a forward stock price. This is one of the standards in market used by market participants to quote volatilities. The volatility of the forward F is described by a parameter \sigma. SABR is a dynamic model in which both F and \sigma are represented by stochastic state variables whose time evolution is given by the following system of stochastic differential equations: :dF_t=\sigma_t \left(F_t\right)^\beta\, dW_t, :d\sigma_t=\a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Stochastic Volatility
In statistics, stochastic volatility models are those in which the variance of a stochastic process is itself randomly distributed. They are used in the field of mathematical finance to evaluate derivative securities, such as options. The name derives from the models' treatment of the underlying security's volatility as a random process, governed by state variables such as the price level of the underlying security, the tendency of volatility to revert to some long-run mean value, and the variance of the volatility process itself, among others. Stochastic volatility models are one approach to resolve a shortcoming of the Black–Scholes model. In particular, models based on Black-Scholes assume that the underlying volatility is constant over the life of the derivative, and unaffected by the changes in the price level of the underlying security. However, these models cannot explain long-observed features of the implied volatility surface such as volatility smile and skew, which ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Volatility (finance)
In finance, volatility (usually denoted by ''σ'') is the degree of variation of a trading price series over time, usually measured by the standard deviation of logarithmic returns. Historic volatility measures a time series of past market prices. Implied volatility looks forward in time, being derived from the market price of a market-traded derivative (in particular, an option). Volatility terminology Volatility as described here refers to the actual volatility, more specifically: * actual current volatility of a financial instrument for a specified period (for example 30 days or 90 days), based on historical prices over the specified period with the last observation the most recent price. * actual historical volatility which refers to the volatility of a financial instrument over a specified period but with the last observation on a date in the past **near synonymous is realized volatility, the square root of the realized variance, in turn calculated using the sum of squ ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Local Volatility
A local volatility model, in mathematical finance and financial engineering, is an option pricing model that treats volatility as a function of both the current asset level S_t and of time t . As such, it is a generalisation of the Black–Scholes model, where the volatility is a constant (i.e. a trivial function of S_t and t ). Formulation In mathematical finance, the asset ''S''''t'' that underlies a financial derivative is typically assumed to follow a stochastic differential equation of the form : dS_t = (r_t-d_t) S_t\,dt + \sigma_t S_t\,dW_t , under the risk neutral measure, where r_t is the instantaneous risk free rate, giving an average local direction to the dynamics, and W_t is a Wiener process, representing the inflow of randomness into the dynamics. The amplitude of this randomness is measured by the instant volatility \sigma_t. In the simplest model i.e. the Black–Scholes model, \sigma_t is assumed to be constant; in reality, the realised volatility of an unde ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Put–call Parity
In financial mathematics, put–call parity defines a relationship between the price of a European call option and European put option, both with the identical strike price and expiry, namely that a portfolio of a long call option and a short put option is equivalent to (and hence has the same value as) a single forward contract at this strike price and expiry. This is because if the price at expiry is above the strike price, the call will be exercised, while if it is below, the put will be exercised, and thus in either case one unit of the asset will be purchased for the strike price, exactly as in a forward contract. The validity of this relationship requires that certain assumptions be satisfied; these are specified and the relationship is derived below. In practice transaction costs and financing costs (leverage) mean this relationship will not exactly hold, but in liquid markets the relationship is close to exact. Assumptions Put–call parity is a static replication, and t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
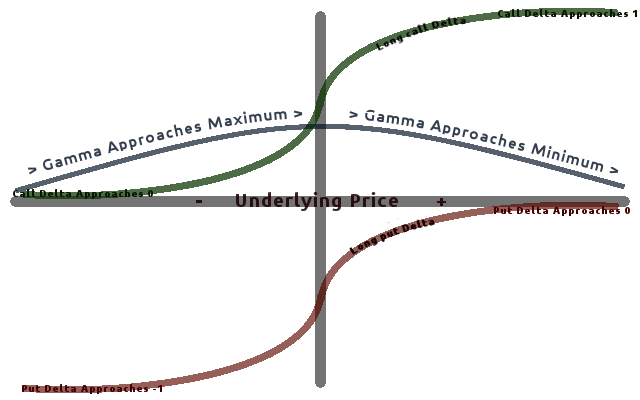
Greeks (finance)
In mathematical finance, the Greeks are the quantities representing the sensitivity of the price of derivatives such as options to a change in underlying parameters on which the value of an instrument or portfolio of financial instruments is dependent. The name is used because the most common of these sensitivities are denoted by Greek letters (as are some other finance measures). Collectively these have also been called the risk sensitivities, risk measures or hedge parameters. Use of the Greeks The Greeks are vital tools in risk management. Each Greek measures the sensitivity of the value of a portfolio to a small change in a given underlying parameter, so that component risks may be treated in isolation, and the portfolio rebalanced accordingly to achieve a desired exposure; see for example delta hedging. The Greeks in the Black–Scholes model are relatively easy to calculate, a desirable property of financial models, and are very useful for derivatives traders, especi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Supply And Demand
In microeconomics, supply and demand is an economic model of price determination in a Market (economics), market. It postulates that, Ceteris paribus, holding all else equal, in a perfect competition, competitive market, the unit price for a particular Good (economics), good, or other traded item such as Labour supply, labor or Market liquidity, liquid financial assets, will vary until it settles at a point where the quantity demanded (at the current price) will equal the quantity supplied (at the current price), resulting in an economic equilibrium for price and quantity transacted. The concept of supply and demand forms the theoretical basis of modern economics. In macroeconomics, as well, the AD–AS model, aggregate demand-aggregate supply model has been used to depict how the quantity of real GDP, total output and the aggregate price level may be determined in equilibrium. Graphical representations Supply schedule A supply schedule, depicted graphically as a supply cu ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |