|
Hopfield Net
A Hopfield network (or Ising model of a neural network or Ising–Lenz–Little model) is a form of recurrent artificial neural network and a type of spin glass system popularised by John Hopfield in 1982 as described earlier by Little in 1974 based on Ernst Ising's work with Wilhelm Lenz on the Ising model. Hopfield networks serve as content-addressable ("associative") memory systems with binary threshold nodes, or with continuous variables. Hopfield networks also provide a model for understanding human memory. Origins The Ising model of a neural network as a memory model was first proposed by William A. Little in 1974, which was acknowledged by Hopfield in his 1982 paper. Networks with continuous dynamics were developed by Hopfield in his 1984 paper. A major advance in memory storage capacity was developed by Krotov and Hopfield in 2016 through a change in network dynamics and energy function. This idea was further extended by Demircigil and collaborators in 2017. The con ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Recurrent Neural Network
A recurrent neural network (RNN) is a class of artificial neural networks where connections between nodes can create a cycle, allowing output from some nodes to affect subsequent input to the same nodes. This allows it to exhibit temporal dynamic behavior. Derived from feedforward neural networks, RNNs can use their internal state (memory) to process variable length sequences of inputs. This makes them applicable to tasks such as unsegmented, connected handwriting recognition or speech recognition. Recurrent neural networks are theoretically Turing complete and can run arbitrary programs to process arbitrary sequences of inputs. The term "recurrent neural network" is used to refer to the class of networks with an infinite impulse response, whereas "convolutional neural network" refers to the class of finite impulse response. Both classes of networks exhibit temporal dynamic behavior. A finite impulse recurrent network is a directed acyclic graph that can be unrolled and replaced ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Lyapunov Function
In the theory of ordinary differential equations (ODEs), Lyapunov functions, named after Aleksandr Lyapunov, are scalar functions that may be used to prove the stability of an equilibrium of an ODE. Lyapunov functions (also called Lyapunov’s second method for stability) are important to stability theory of dynamical systems and control theory. A similar concept appears in the theory of general state space Markov chains, usually under the name Foster–Lyapunov functions. For certain classes of ODEs, the existence of Lyapunov functions is a necessary and sufficient condition for stability. Whereas there is no general technique for constructing Lyapunov functions for ODEs, in many specific cases the construction of Lyapunov functions is known. For instance, quadratic functions suffice for systems with one state; the solution of a particular linear matrix inequality provides Lyapunov functions for linear systems; and conservation laws can often be used to construct Lyapunov f ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
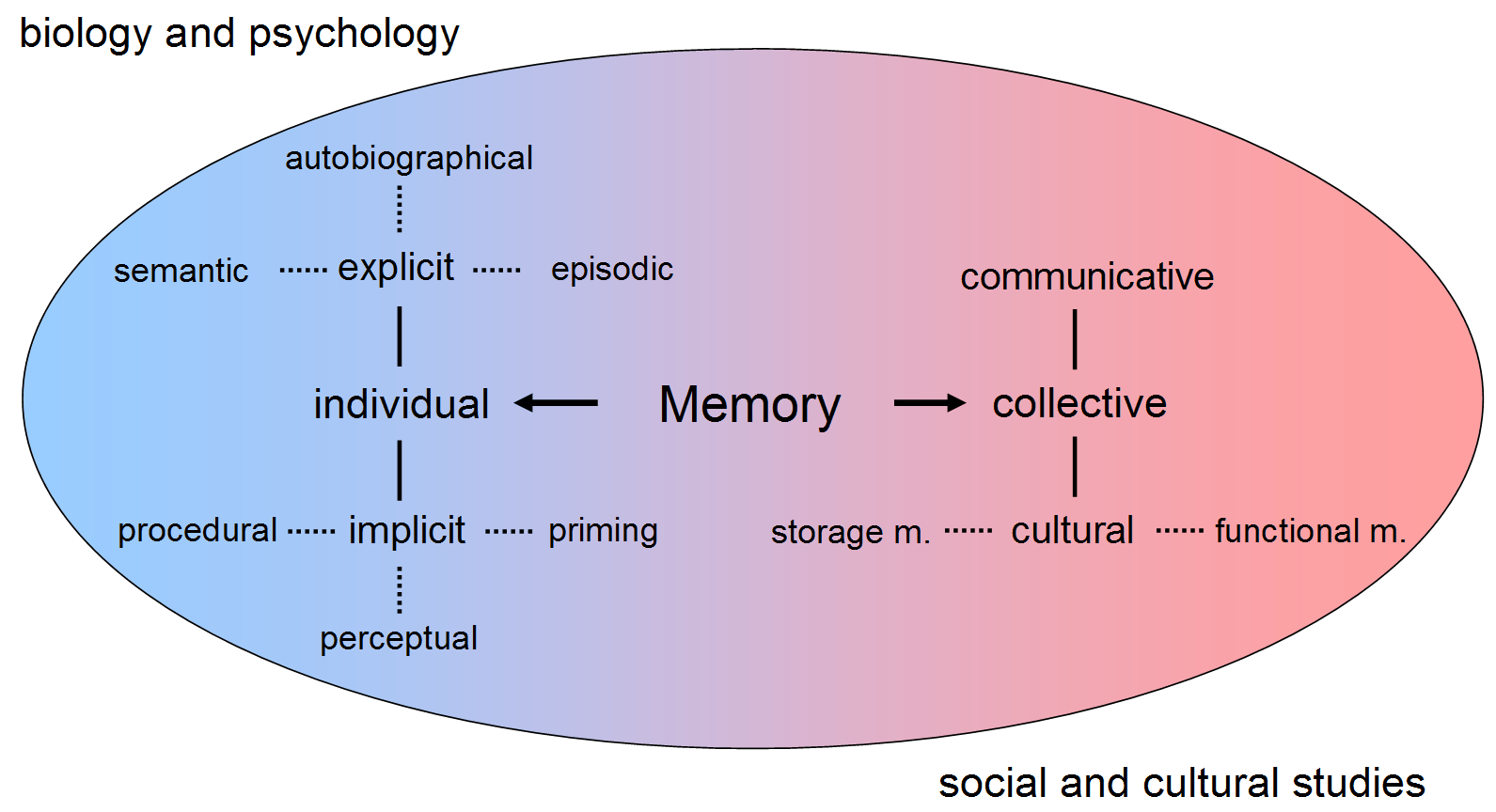
Memory
Memory is the faculty of the mind by which data or information is encoded, stored, and retrieved when needed. It is the retention of information over time for the purpose of influencing future action. If past events could not be remembered, it would be impossible for language, relationships, or personal identity to develop. Memory loss is usually described as forgetfulness or amnesia. Memory is often understood as an informational processing system with explicit and implicit functioning that is made up of a sensory processor, short-term (or working) memory, and long-term memory. This can be related to the neuron. The sensory processor allows information from the outside world to be sensed in the form of chemical and physical stimuli and attended to various levels of focus and intent. Working memory serves as an encoding and retrieval processor. Information in the form of stimuli is encoded in accordance with explicit or implicit functions by the working memory proces ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Association (psychology)
Association in psychology refers to a mental connection between concepts, events, or mental states that usually stems from specific experiences.Klein, Stephen (2012). ''Learning: Principles and Applications'' (6 ed.). SAGE Publications. . Associations are seen throughout several schools of thought in psychology including behaviorism, associationism, psychoanalysis, social psychology, and structuralism. The idea stems from Plato and Aristotle, especially with regard to the succession of memories, and it was carried on by philosophers such as John Locke, David Hume, David Hartley, and James Mill.Boring, E. G. (1950) It finds its place in modern psychology in such areas as memory, learning, and the study of neural pathways. Learned associations Associative learning is when a subject creates a relationship between stimuli (e.g. auditory or visual) or behavior and the original stimulus. The higher the concreteness of stimulus items, the more likely are they to evoke sens ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
One-shot Learning (software)
One-shot learning is an object categorization problem, found mostly in computer vision. Whereas most machine learning-based object categorization algorithms require training on hundreds or thousands of examples, one-shot learning aims to classify objects from one, or only a few, examples. The term few-shot learning is also used for these problems, especially when more than one example is needed. Motivation The ability to learn object categories from few examples, and at a rapid pace, has been demonstrated in humans. It is estimated that a child learns almost all of the 10 ~ 30 thousand object categories in the world by age six. This is due not only to the human mind's computational power, but also to its ability to synthesize and learn new object categories from existing information about different, previously learned categories. Given two examples from two object categories: one, an unknown object composed of familiar shapes, the second, an unknown, amorphous shape; it is much e ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Amos Storkey
Amos James Storkey is Professor of Machine Learning and Artificial Intelligence at the School of Informatics, University of Edinburgh. Storkey studied mathematics at Trinity College, Cambridge and obtained his doctorate from Imperial College, London. In 1997 during his PhD, he worked on the Hopfield Network a form of recurrent artificial neural network popularized by John Hopfield in 1982. Hopfield nets serve as content-addressable ("associative") memory systems with binary threshold nodes and Storkey developed what became known as the "Storkey Learning Rule" .Storkey, Amos. "Increasing the capacity of a Hopfield network without sacrificing functionality." Artificial Neural Networks – ICANN'97 (1997)451-456Storkey, Amos. "Efficient Covariance Matrix Methods for Bayesian Gaussian Processes and Hopfield Neural Networks". PhD Thesis. University of London. (1999) Subsequently, he has worked on approximate Bayesian methods, machine learning in astronomy, graphical models, infe ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Learning Rule
An artificial neural network's learning rule or learning process is a method, mathematical logic or algorithm which improves the network's performance and/or training time. Usually, this rule is applied repeatedly over the network. It is done by updating the weights and bias levels of a network when a network is simulated in a specific data environment. A learning rule may accept existing conditions (weights and biases) of the network and will compare the expected result and actual result of the network to give new and improved values for weights and bias. Depending on the complexity of actual model being simulated, the learning rule of the network can be as simple as an XOR gate or mean squared error, or as complex as the result of a system of differential equations. The learning rule is one of the factors which decides how fast or how accurately the artificial network can be developed. Depending upon the process to develop the network there are three main models of machine l ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Perceptron
In machine learning, the perceptron (or McCulloch-Pitts neuron) is an algorithm for supervised learning of binary classifiers. A binary classifier is a function which can decide whether or not an input, represented by a vector of numbers, belongs to some specific class. It is a type of linear classifier, i.e. a classification algorithm that makes its predictions based on a linear predictor function combining a set of weights with the feature vector. History The perceptron was invented in 1943 by McCulloch and Pitts. The first implementation was a machine built in 1958 at the Cornell Aeronautical Laboratory by Frank Rosenblatt, funded by the United States Office of Naval Research. The perceptron was intended to be a machine, rather than a program, and while its first implementation was in software for the IBM 704, it was subsequently implemented in custom-built hardware as the "Mark 1 perceptron". This machine was designed for image recognition: it had an array of 400 photoc ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Nonlinear Dynamical System
In mathematics, a dynamical system is a system in which a function describes the time dependence of a point in an ambient space. Examples include the mathematical models that describe the swinging of a clock pendulum, the flow of water in a pipe, the random motion of particles in the air, and the number of fish each springtime in a lake. The most general definition unifies several concepts in mathematics such as ordinary differential equations and ergodic theory by allowing different choices of the space and how time is measured. Time can be measured by integers, by real or complex numbers or can be a more general algebraic object, losing the memory of its physical origin, and the space may be a manifold or simply a set, without the need of a smooth space-time structure defined on it. At any given time, a dynamical system has a state representing a point in an appropriate state space. This state is often given by a tuple of real numbers or by a vector in a geometrical ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Markov Property
In probability theory and statistics, the term Markov property refers to the memoryless property of a stochastic process. It is named after the Russian mathematician Andrey Markov. The term strong Markov property is similar to the Markov property, except that the meaning of "present" is defined in terms of a random variable known as a stopping time. The term Markov assumption is used to describe a model where the Markov assumption is assumed to hold, such as a hidden Markov model. A Markov random field extends this property to two or more dimensions or to random variables defined for an interconnected network of items. An example of a model for such a field is the Ising model. A discrete-time stochastic process satisfying the Markov property is known as a Markov chain. Introduction A stochastic process has the Markov property if the conditional probability distribution of future states of the process (conditional on both past and present values) depends only upon the presen ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Gibbs Measure
In mathematics, the Gibbs measure, named after Josiah Willard Gibbs, is a probability measure frequently seen in many problems of probability theory and statistical mechanics. It is a generalization of the canonical ensemble to infinite systems. The canonical ensemble gives the probability of the system ''X'' being in state ''x'' (equivalently, of the random variable ''X'' having value ''x'') as :P(X=x) = \frac \exp ( - \beta E(x)). Here, is a function from the space of states to the real numbers; in physics applications, is interpreted as the energy of the configuration ''x''. The parameter is a free parameter; in physics, it is the inverse temperature. The normalizing constant is the partition function. However, in infinite systems, the total energy is no longer a finite number and cannot be used in the traditional construction of the probability distribution of a canonical ensemble. Traditional approaches in statistical physics studied the limit of intensive properties as ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |