|
Honeycomb Conjecture
The honeycomb conjecture states that a regular hexagonal grid or honeycomb has the least total perimeter of any subdivision of the plane into regions of equal area. The conjecture was proven in 1999 by mathematician Thomas C. Hales. Theorem Let \Gamma be any system of smooth curves in \mathbb^2, subdividing the plane into regions (connected components of the complement of \Gamma) all of which are bounded and have unit area. Then, averaged over large disks in the plane, the average length of \Gamma per unit area is at least as large as for the hexagon tiling. The theorem applies even if the complement of \Gamma has additional components that are unbounded or whose area is not one; allowing these additional components cannot shorten \Gamma. Formally, let B(0,r) denote the disk of radius r centered at the origin, let L_r denote the total length of \Gamma\cap B(0,r), and let A_r denote the total area of B(0,r) covered by bounded unit-area components. (If these are the only components, ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Hexagons
In geometry, a hexagon (from Greek , , meaning "six", and , , meaning "corner, angle") is a six-sided polygon. The total of the internal angles of any simple (non-self-intersecting) hexagon is 720°. Regular hexagon A '' regular hexagon'' has Schläfli symbol and can also be constructed as a truncated equilateral triangle, t, which alternates two types of edges. A regular hexagon is defined as a hexagon that is both equilateral and equiangular. It is bicentric, meaning that it is both cyclic (has a circumscribed circle) and tangential (has an inscribed circle). The common length of the sides equals the radius of the circumscribed circle or circumcircle, which equals \tfrac times the apothem (radius of the inscribed circle). All internal angles are 120 degrees. A regular hexagon has six rotational symmetries (''rotational symmetry of order six'') and six reflection symmetries (''six lines of symmetry''), making up the dihedral group D6. The longest diagonals of a regul ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Hexagonal
In geometry, a hexagon (from Greek , , meaning "six", and , , meaning "corner, angle") is a six-sided polygon. The total of the internal angles of any simple (non-self-intersecting) hexagon is 720°. Regular hexagon A '' regular hexagon'' has Schläfli symbol and can also be constructed as a truncated equilateral triangle, t, which alternates two types of edges. A regular hexagon is defined as a hexagon that is both equilateral and equiangular. It is bicentric, meaning that it is both cyclic (has a circumscribed circle) and tangential (has an inscribed circle). The common length of the sides equals the radius of the circumscribed circle or circumcircle, which equals \tfrac times the apothem (radius of the inscribed circle). All internal angles are 120 degrees. A regular hexagon has six rotational symmetries (''rotational symmetry of order six'') and six reflection symmetries (''six lines of symmetry''), making up the dihedral group D6. The longest diagonals of a regular ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Discrete Geometry
Discrete geometry and combinatorial geometry are branches of geometry that study combinatorial properties and constructive methods of discrete geometric objects. Most questions in discrete geometry involve finite or discrete sets of basic geometric objects, such as points, lines, planes, circles, spheres, polygons, and so forth. The subject focuses on the combinatorial properties of these objects, such as how they intersect one another, or how they may be arranged to cover a larger object. Discrete geometry has a large overlap with convex geometry and computational geometry, and is closely related to subjects such as finite geometry, combinatorial optimization, digital geometry, discrete differential geometry, geometric graph theory, toric geometry, and combinatorial topology. History Although polyhedra and tessellations had been studied for many years by people such as Kepler and Cauchy, modern discrete geometry has its origins in the late 19th century. Early topics studie ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
William Thomson, 1st Baron Kelvin
William Thomson, 1st Baron Kelvin, (26 June 182417 December 1907) was a British mathematician, mathematical physicist and engineer born in Belfast. Professor of Natural Philosophy at the University of Glasgow for 53 years, he did important work in the mathematical analysis of electricity and formulation of the first and second laws of thermodynamics, and did much to unify the emerging discipline of physics in its contemporary form. He received the Royal Society's Copley Medal in 1883, was its president 1890–1895, and in 1892 was the first British scientist to be elevated to the House of Lords. Absolute temperatures are stated in units of kelvin in his honour. While the existence of a coldest possible temperature ( absolute zero) was known prior to his work, Kelvin is known for determining its correct value as approximately −273.15 degrees Celsius or −459.67 degrees Fahrenheit. The Joule–Thomson effect is also named in his honour. He worked closely with mathematics ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
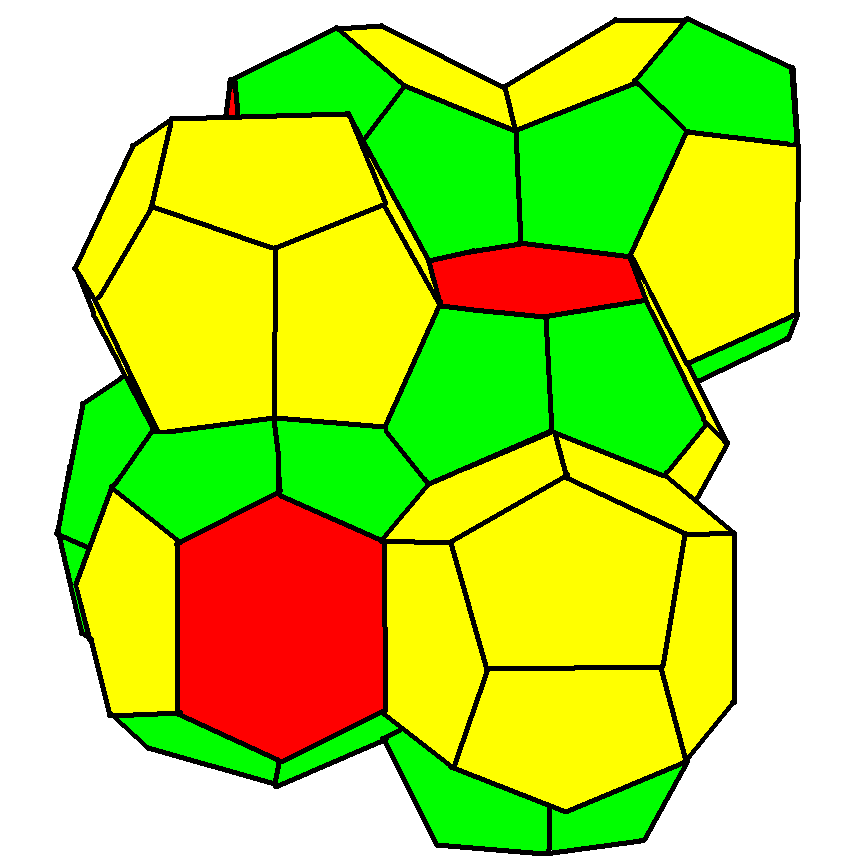
Weaire–Phelan Structure
In geometry, the Weaire–Phelan structure is a three-dimensional structure representing an idealised foam of equal-sized bubbles, with two different shapes. In 1993, Denis Weaire and Robert Phelan found that this structure was a better solution of the Kelvin problem of tiling space by equal volume cells of minimum surface area than the previous best-known solution, the Kelvin structure. History and the Kelvin problem In two dimensions, the subdivision of the plane into cells of equal area with minimum average perimeter is given by the hexagonal tiling, but although the first record of this honeycomb conjecture goes back to the ancient Roman scholar Marcus Terentius Varro, it was not proven until the work of Thomas C. Hales in 1999. In 1887, Lord Kelvin asked the corresponding question for three-dimensional space: how can space be partitioned into cells of equal volume with the least area of surface between them? Or, in short, what was the most efficient soap bubble foam? This ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Circle Packing
In geometry, circle packing is the study of the arrangement of circles (of equal or varying sizes) on a given surface such that no overlapping occurs and so that no circle can be enlarged without creating an overlap. The associated ''packing density'', ''η'', of an arrangement is the proportion of the surface covered by the circles. Generalisations can be made to higher dimensions – this is called ''sphere packing'', which usually deals only with identical spheres. The branch of mathematics generally known as "circle packing" is concerned with the geometry and combinatorics of packings of arbitrarily-sized circles: these give rise to discrete analogs of conformal mapping, Riemann surfaces and the like. Densest packing In the two-dimensional Euclidean plane, Joseph Louis Lagrange proved in 1773 that the highest-density lattice packing of circles is the hexagonal packing arrangement, in which the centres of the circles are arranged in a hexagonal lattice (staggered rows, ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
MathWorld
''MathWorld'' is an online mathematics reference work, created and largely written by Eric W. Weisstein. It is sponsored by and licensed to Wolfram Research, Inc. and was partially funded by the National Science Foundation's National Science Digital Library grant to the University of Illinois at Urbana–Champaign. History Eric W. Weisstein, the creator of the site, was a physics and astronomy student who got into the habit of writing notes on his mathematical readings. In 1995 he put his notes online and called it "Eric's Treasure Trove of Mathematics." It contained hundreds of pages/articles, covering a wide range of mathematical topics. The site became popular as an extensive single resource on mathematics on the web. Weisstein continuously improved the notes and accepted corrections and comments from online readers. In 1998, he made a contract with CRC Press and the contents of the site were published in print and CD-ROM form, titled "CRC Concise Encyclopedia of Mathematic ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Convex Polygon
In geometry, a convex polygon is a polygon that is the boundary of a convex set. This means that the line segment between two points of the polygon is contained in the union of the interior and the boundary of the polygon. In particular, it is a simple polygon (not self-intersecting). Equivalently, a polygon is convex if every line that does not contain any edge intersects the polygon in at most two points. A strictly convex polygon is a convex polygon such that no line contains two of its edges. In a convex polygon, all interior angles are less than or equal to 180 degrees, while in a strictly convex polygon all interior angles are strictly less than 180 degrees. Properties The following properties of a simple polygon are all equivalent to convexity: *Every internal angle is strictly less than 180 degrees. *Every point on every line segment between two points inside or on the boundary of the polygon remains inside or on the boundary. *The polygon is entirely contained in ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
László Fejes Tóth
László Fejes Tóth ( hu, Fejes Tóth László, 12 March 1915 – 17 March 2005) was a Hungarian mathematician who specialized in geometry. He proved that a lattice pattern is the most efficient way to pack centrally symmetric convex sets on the Euclidean plane (a generalization of Thue's theorem, a 2-dimensional analog of the Kepler conjecture). He also investigated the sphere packing problem. He was the first to show, in 1953, that proof of the Kepler conjecture can be reduced to a finite case analysis and, later, that the problem might be solved using a computer. He was a member of the Hungarian Academy of Sciences (from 1962) and a director of the Alfréd Rényi Institute of Mathematics (1970-1983). He received both the Kossuth Prize (1957) and State Award (1973). Together with H.S.M. Coxeter and Paul Erdős, he laid the foundations of discrete geometry. Early life and career As described in a 1999 interview witIstván Hargittai Fejes Tóth's father was a railway ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Jan Brożek
Jan Brożek (''Ioannes Broscius'', ''Joannes Broscius'' or ''Johannes Broscius''; 1 November 1585 – 21 November 1652) was a Polish polymath: a mathematician, astronomer, physician, poet, writer, musician and rector of the Kraków Academy. Life Brożek was born in Kurzelów, Sandomierz Province, and lived in Kraków, Staszów, and Międzyrzec Podlaski. He received his primary education in Kurzelow, then continued education in Krakow. In 1604, he enrolled in the Faculty of Liberal Art at the Kraków Academy (now Jagiellonian University), where he received his baccalaureate on 30 March 1605. In January 1614, he became the head of the Astronomy and Astrology Faculty. From 1620 to 1624, he stayed in Padua, where he studied medicine at the University of Padua and received his doctorate in medicine on 11 August 1623. He served as rector of Jagiellonian University. He was the most prominent Polish mathematician of the 17th century, working on the theory of numbers (particularly perf ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Triangular Tiling Circle Packing
A triangle is a polygon with three edges and three vertices. It is one of the basic shapes in geometry. A triangle with vertices ''A'', ''B'', and ''C'' is denoted \triangle ABC. In Euclidean geometry, any three points, when non-collinear, determine a unique triangle and simultaneously, a unique plane (i.e. a two-dimensional Euclidean space). In other words, there is only one plane that contains that triangle, and every triangle is contained in some plane. If the entire geometry is only the Euclidean plane, there is only one plane and all triangles are contained in it; however, in higher-dimensional Euclidean spaces, this is no longer true. This article is about triangles in Euclidean geometry, and in particular, the Euclidean plane, except where otherwise noted. Types of triangle The terminology for categorizing triangles is more than two thousand years old, having been defined on the very first page of Euclid's Elements. The names used for modern classification are eit ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Pappus Of Alexandria
Pappus of Alexandria (; grc-gre, Πάππος ὁ Ἀλεξανδρεύς; AD) was one of the last great Greek mathematicians of antiquity known for his ''Synagoge'' (Συναγωγή) or ''Collection'' (), and for Pappus's hexagon theorem in projective geometry. Nothing is known of his life, other than what can be found in his own writings: that he had a son named Hermodorus, and was a teacher in Alexandria.Pierre Dedron, J. Itard (1959) ''Mathematics And Mathematicians'', Vol. 1, p. 149 (trans. Judith V. Field) (Transworld Student Library, 1974) ''Collection'', his best-known work, is a compendium of mathematics in eight volumes, the bulk of which survives. It covers a wide range of topics, including geometry, recreational mathematics, doubling the cube, polygons and polyhedra. Context Pappus was active in the 4th century AD. In a period of general stagnation in mathematical studies, he stands out as a remarkable exception. "How far he was above his contemporaries, how lit ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |