|
Hilbert Basis (linear Programming)
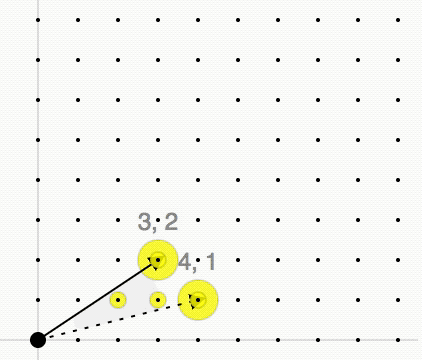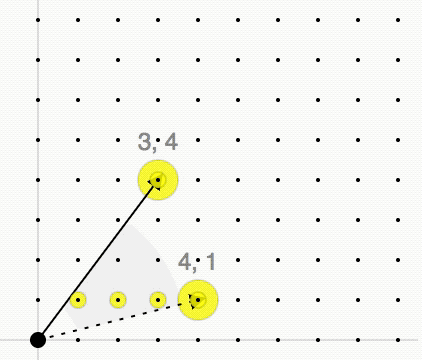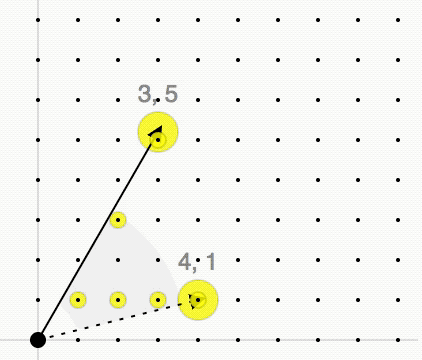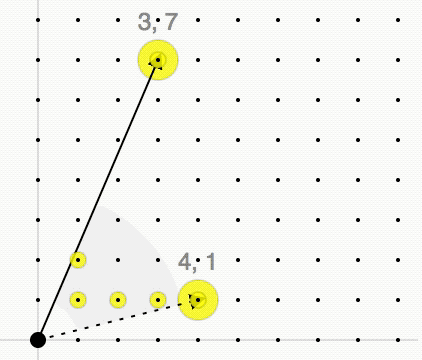
The Hilbert basis of a convex cone ''C'' is a minimal set of integer vectors such that every integer vector in ''C'' is a conical combination of the vectors in the Hilbert basis with integer coefficients. Definition Given a lattice L\subset\mathbb^d and a convex polyhedral cone with generators a_1,\ldots,a_n\in\mathbb^d :C=\\subset\mathbb^d we consider the monoid C\cap L. By Gordan's lemma Gordan's lemma is a lemma in convex geometry and algebraic geometry. It can be stated in several ways. * Let A be a matrix of integers. Let M be the set of non-negative integer solutions of A \cdot x = 0. Then there exists a finite subset of vector ... this monoid is finitely generated, i.e., there exists a finite set of lattice points \\subset C\cap L such that every lattice point x\in C\cap L is an integer conical combination of these points: : x=\lambda_1 x_1+\ldots+\lambda_m x_m, \quad\lambda_1,\ldots,\lambda_m\in\mathbb, \lambda_1,\ldots,\lambda_m\geq0 The cone ''C'' is called pointed ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Convex Cone
In linear algebra, a ''cone''—sometimes called a linear cone for distinguishing it from other sorts of cones—is a subset of a vector space that is closed under scalar multiplication; that is, is a cone if x\in C implies sx\in C for every . When the scalars are real numbers, or belong to an ordered field, one generally calls a cone a subset of a vector space that is closed under multiplication by a ''positive scalar''. In this context, a convex cone is a cone that is closed under addition, or, equivalently, a subset of a vector space that is closed under linear combinations with positive coefficients. It follows that convex cones are convex sets. In this article, only the case of scalars in an ordered field is considered. Definition A subset ''C'' of a vector space ''V'' over an ordered field ''F'' is a cone (or sometimes called a linear cone) if for each ''x'' in ''C'' and positive scalar ''α'' in ''F'', the product ''αx'' is in ''C''. Note that some authors define co ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Vector (mathematics)
In mathematics and physics, vector is a term that refers colloquially to some quantities that cannot be expressed by a single number (a scalar), or to elements of some vector spaces. Historically, vectors were introduced in geometry and physics (typically in mechanics) for quantities that have both a magnitude and a direction, such as displacements, forces and velocity. Such quantities are represented by geometric vectors in the same way as distances, masses and time are represented by real numbers. The term ''vector'' is also used, in some contexts, for tuples, which are finite sequences of numbers of a fixed length. Both geometric vectors and tuples can be added and scaled, and these vector operations led to the concept of a vector space, which is a set equipped with a vector addition and a scalar multiplication that satisfy some axioms generalizing the main properties of operations on the above sorts of vectors. A vector space formed by geometric vectors is called a Euclidean ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Conical Combination
Given a finite number of vectors x_1, x_2, \dots, x_n in a real vector space, a conical combination, conical sum, or weighted sum''Convex Analysis and Minimization Algorithms'' by Jean-Baptiste Hiriart-Urruty, Claude Lemaréchal, 1993, pp. 101, 102/ref>''Mathematical Programming'', by Melvyn W. Jeter (1986) p. 68/ref> of these vectors is a vector of the form : \alpha_1x_1+\alpha_2x_2+\cdots+\alpha_nx_n where \alpha_i are non-negative real numbers. The name derives from the fact that a conical sum of vectors defines a cone (possibly in a lower-dimensional subspace). Conical hull The set of all conical combinations for a given set ''S'' is called the conical hull of ''S'' and denoted ''cone''(''S'') or ''coni''(''S''). That is, :\operatorname (S)=\left\. By taking ''k'' = 0, it follows the zero vector (origin) belongs to all conical hulls (since the summation becomes an empty sum). The conical hull of a set ''S'' is a convex set. In fact, it is the intersection o ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Hilbert Basis
Hilbert basis may refer to * In Invariant theory, a finite set of invariant polynomials, such that every invariant polynomial may be written as a polynomial function of these basis elements * Orthonormal basis of a Hilbert space * Hilbert basis (linear programming) The Hilbert basis of a convex cone ''C'' is a minimal set of integer vectors such that every integer vector in ''C'' is a conical combination of the vectors in the Hilbert basis with integer coefficients. Definition Given a lattice L\subset\math ... * Hilbert's basis theorem {{mathdab ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Lattice (group)
In geometry and group theory, a lattice in the real coordinate space \mathbb^n is an infinite set of points in this space with the properties that coordinate wise addition or subtraction of two points in the lattice produces another lattice point, that the lattice points are all separated by some minimum distance, and that every point in the space is within some maximum distance of a lattice point. Closure under addition and subtraction means that a lattice must be a subgroup of the additive group of the points in the space, and the requirements of minimum and maximum distance can be summarized by saying that a lattice is a Delone set. More abstractly, a lattice can be described as a free abelian group of dimension n which spans the vector space \mathbb^n. For any basis of \mathbb^n, the subgroup of all linear combinations with integer coefficients of the basis vectors forms a lattice, and every lattice can be formed from a basis in this way. A lattice may be viewed as a regula ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Monoid
In abstract algebra, a branch of mathematics, a monoid is a set equipped with an associative binary operation and an identity element. For example, the nonnegative integers with addition form a monoid, the identity element being 0. Monoids are semigroups with identity. Such algebraic structures occur in several branches of mathematics. The functions from a set into itself form a monoid with respect to function composition. More generally, in category theory, the morphisms of an object to itself form a monoid, and, conversely, a monoid may be viewed as a category with a single object. In computer science and computer programming, the set of strings built from a given set of characters is a free monoid. Transition monoids and syntactic monoids are used in describing finite-state machines. Trace monoids and history monoids provide a foundation for process calculi and concurrent computing. In theoretical computer science, the study of monoids is fundamental for automata ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Gordan's Lemma
Gordan's lemma is a lemma in convex geometry and algebraic geometry. It can be stated in several ways. * Let A be a matrix of integers. Let M be the set of non-negative integer solutions of A \cdot x = 0. Then there exists a finite subset of vectors in M, such that every element of M is a linear combination of these vectors with non-negative integer coefficients. * The semigroup of integral points in a rational convex polyhedral cone is finitely generated. * An affine toric variety is an algebraic variety (this follows from the fact that the prime spectrum of the semigroup algebra of such a semigroup is, by definition, an affine toric variety). The lemma is named after the mathematician Paul Gordan (1837–1912). Some authors have misspelled it as "Gordon's lemma". Proofs There are topological and algebraic proofs. Topological proof Let \sigma be the dual cone of the given rational polyhedral cone. Let u_1, \dots, u_r be integral vectors so that \sigma = \. Then the u_i's g ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Journal Für Die Reine Und Angewandte Mathematik
''Crelle's Journal'', or just ''Crelle'', is the common name for a mathematics journal, the ''Journal für die reine und angewandte Mathematik'' (in English: ''Journal for Pure and Applied Mathematics''). History The journal was founded by August Leopold Crelle (Berlin) in 1826 and edited by him until his death in 1855. It was one of the first major mathematical journals that was not a proceedings of an academy. It has published many notable papers, including works of Niels Henrik Abel, Georg Cantor, Gotthold Eisenstein, Carl Friedrich Gauss and Otto Hesse. It was edited by Carl Wilhelm Borchardt from 1856 to 1880, during which time it was known as ''Borchardt's Journal''. The current editor-in-chief is Rainer Weissauer (Ruprecht-Karls-Universität Heidelberg) Past editors * 1826–1856 August Leopold Crelle * 1856–1880 Carl Wilhelm Borchardt * 1881–1888 Leopold Kronecker, Karl Weierstrass * 1889–1892 Leopold Kronecker * 1892–1902 Lazarus Fuchs * 1903–1928 Kurt Hens ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Linear Programming
Linear programming (LP), also called linear optimization, is a method to achieve the best outcome (such as maximum profit or lowest cost) in a mathematical model whose requirements are represented by linear function#As a polynomial function, linear relationships. Linear programming is a special case of mathematical programming (also known as mathematical optimization). More formally, linear programming is a technique for the mathematical optimization, optimization of a linear objective function, subject to linear equality and linear inequality Constraint (mathematics), constraints. Its feasible region is a convex polytope, which is a set defined as the intersection (mathematics), intersection of finitely many Half-space (geometry), half spaces, each of which is defined by a linear inequality. Its objective function is a real number, real-valued affine function, affine (linear) function defined on this polyhedron. A linear programming algorithm finds a point in the polytope where ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |