|
Hidden Markov Models
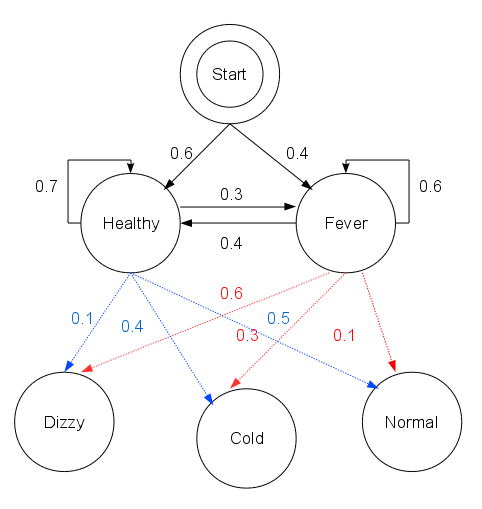
A hidden Markov model (HMM) is a statistical Markov model in which the system being modeled is assumed to be a Markov process — call it X — with unobservable ("''hidden''") states. As part of the definition, HMM requires that there be an observable process Y whose outcomes are "influenced" by the outcomes of X in a known way. Since X cannot be observed directly, the goal is to learn about X by observing Y. HMM has an additional requirement that the outcome of Y at time t=t_0 must be "influenced" exclusively by the outcome of X at t=t_0 and that the outcomes of X and Y at t handwriting recognition, handwriting, gesture recognition, part-of-speech tagging, musical score following, partial discharges and bioinformatics. Definition Let X_n and Y_n be discrete-time stochastic processes and n\geq 1. The pair (X_n,Y_n) is a ''hidden Markov model'' if * X_n is a Markov process whose behavior is not directly observable ("hidden"); * \operatorname\bigl(Y_n \in A ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Statistical Model
A statistical model is a mathematical model that embodies a set of statistical assumptions concerning the generation of Sample (statistics), sample data (and similar data from a larger Statistical population, population). A statistical model represents, often in considerably idealized form, the data-generating process. A statistical model is usually specified as a mathematical relationship between one or more random variables and other non-random variables. As such, a statistical model is "a formal representation of a theory" (Herman J. Adèr, Herman Adèr quoting Kenneth A. Bollen, Kenneth Bollen). All Statistical hypothesis testing, statistical hypothesis tests and all Estimator, statistical estimators are derived via statistical models. More generally, statistical models are part of the foundation of statistical inference. Introduction Informally, a statistical model can be thought of as a statistical assumption (or set of statistical assumptions) with a certain property: that ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Partial Discharge
In electrical engineering, partial discharge (PD) is a localized dielectric breakdown (DB) (which does not completely bridge the space between the two conductors) of a small portion of a solid or fluid electrical insulation (EI) system under high voltage (HV) stress. While a corona discharge (CD) is usually revealed by a relatively steady glow or brush discharge (BD) in air, partial discharges within solid insulation system are not visible. PD can occur in a gaseous, liquid, or solid insulating medium. It often starts within gas voids, such as voids in solid epoxy insulation or bubbles in transformer oil. Protracted partial discharge can erode solid insulation and eventually lead to breakdown of insulation. Discharge mechanism PD usually begins within voids, cracks, or inclusions within a solid dielectric, at conductor-dielectric interfaces within solid or liquid dielectrics, or in bubbles within liquid dielectrics. Since PDs are limited to only a portion of the insulation, ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Markov Property
In probability theory and statistics, the term Markov property refers to the memoryless property of a stochastic process. It is named after the Russian mathematician Andrey Markov. The term strong Markov property is similar to the Markov property, except that the meaning of "present" is defined in terms of a random variable known as a stopping time. The term Markov assumption is used to describe a model where the Markov assumption is assumed to hold, such as a hidden Markov model. A Markov random field extends this property to two or more dimensions or to random variables defined for an interconnected network of items. An example of a model for such a field is the Ising model. A discrete-time stochastic process satisfying the Markov property is known as a Markov chain. Introduction A stochastic process has the Markov property if the conditional probability distribution of future states of the process (conditional on both past and present values) depends only upon the present ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Conditional Probability Distribution
In probability theory and statistics, given two jointly distributed random variables X and Y, the conditional probability distribution of Y given X is the probability distribution of Y when X is known to be a particular value; in some cases the conditional probabilities may be expressed as functions containing the unspecified value x of X as a parameter. When both X and Y are categorical variables, a conditional probability table is typically used to represent the conditional probability. The conditional distribution contrasts with the marginal distribution of a random variable, which is its distribution without reference to the value of the other variable. If the conditional distribution of Y given X is a continuous distribution, then its probability density function is known as the conditional density function. The properties of a conditional distribution, such as the moments, are often referred to by corresponding names such as the conditional mean and conditional variance. Mo ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Trellis (graph)
A trellis is a graph whose nodes are ordered into vertical slices (''time'') with each node at each time connected to at least one node at an earlier and at least one node at a later time. The earliest and latest times in the trellis have only one node. Trellises are used in encoders and decoders for communication theory and encryption. They are also the central datatype used in Baum–Welch algorithm or the Viterbi AlgorithmRyan, M. S., & Nudd, G. R. (1993). The viterbi algorithm. University of Warwick, Department of Computer Science. for Hidden Markov Models. The trellis graph is named for its similar appearance to an architectural trellis. References See also * Trellis modulation * Trellis quantization Trellis quantization is an algorithm that can improve data compression in DCT-based encoding methods. It is used to optimize residual DCT coefficients after motion estimation in lossy video compression encoders such as Xvid and x264. Trellis qu ... Application-specif ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Viterbi Algorithm
The Viterbi algorithm is a dynamic programming algorithm for obtaining the maximum a posteriori probability estimate of the most likely sequence of hidden states—called the Viterbi path—that results in a sequence of observed events, especially in the context of Markov information sources and hidden Markov models (HMM). The algorithm has found universal application in decoding the convolutional codes used in both CDMA and GSM digital cellular, dial-up modems, satellite, deep-space communications, and 802.11 wireless LANs. It is now also commonly used in speech recognition, speech synthesis, diarization, keyword spotting, computational linguistics, and bioinformatics. For example, in speech-to-text (speech recognition), the acoustic signal is treated as the observed sequence of events, and a string of text is considered to be the "hidden cause" of the acoustic signal. The Viterbi algorithm finds the most likely string of text given the acoustic signal. History The Viterbi a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Python Programming Language
Python is a high-level, general-purpose programming language. Its design philosophy emphasizes code readability with the use of significant indentation. Python is dynamically-typed and garbage-collected. It supports multiple programming paradigms, including structured (particularly procedural), object-oriented and functional programming. It is often described as a "batteries included" language due to its comprehensive standard library. Guido van Rossum began working on Python in the late 1980s as a successor to the ABC programming language and first released it in 1991 as Python 0.9.0. Python 2.0 was released in 2000 and introduced new features such as list comprehensions, cycle-detecting garbage collection, reference counting, and Unicode support. Python 3.0, released in 2008, was a major revision that is not completely backward-compatible with earlier versions. Python 2 was discontinued with version 2.7.18 in 2020. Python consistently ran ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Hidden Markov Model
A hidden Markov model (HMM) is a statistical Markov model in which the system being modeled is assumed to be a Markov process — call it X — with unobservable ("''hidden''") states. As part of the definition, HMM requires that there be an observable process Y whose outcomes are "influenced" by the outcomes of X in a known way. Since X cannot be observed directly, the goal is to learn about X by observing Y. HMM has an additional requirement that the outcome of Y at time t=t_0 must be "influenced" exclusively by the outcome of X at t=t_0 and that the outcomes of X and Y at t handwriting recognition, handwriting, gesture recognition, part-of-speech tagging, musical score following, partial discharges and bioinformatics. Definition Let X_n and Y_n be discrete-time stochastic processes and n\geq 1. The pair (X_n,Y_n) is a ''hidden Markov model'' if * X_n is a Markov process whose behavior is not directly observable ("hidden"); * \operatorname\bigl(Y_n \i ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Markov Chain
A Markov chain or Markov process is a stochastic model describing a sequence of possible events in which the probability of each event depends only on the state attained in the previous event. Informally, this may be thought of as, "What happens next depends only on the state of affairs ''now''." A countably infinite sequence, in which the chain moves state at discrete time steps, gives a discrete-time Markov chain (DTMC). A continuous-time process is called a continuous-time Markov chain (CTMC). It is named after the Russian mathematician Andrey Markov. Markov chains have many applications as statistical models of real-world processes, such as studying cruise control systems in motor vehicles, queues or lines of customers arriving at an airport, currency exchange rates and animal population dynamics. Markov processes are the basis for general stochastic simulation methods known as Markov chain Monte Carlo, which are used for simulating sampling from complex probability dist ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Urn Problem
In probability and statistics, an urn problem is an idealized mental exercise in which some objects of real interest (such as atoms, people, cars, etc.) are represented as colored balls in an urn or other container. One pretends to remove one or more balls from the urn; the goal is to determine the probability of drawing one color or another, or some other properties. A number of important variations are described below. An urn model is either a set of probabilities that describe events within an urn problem, or it is a probability distribution, or a family of such distributions, of random variables associated with urn problems.Dodge, Yadolah (2003) ''Oxford Dictionary of Statistical Terms'', OUP. History In ''Ars Conjectandi'' (1713), Jacob Bernoulli considered the problem of determining, given a number of pebbles drawn from an urn, the proportions of different colored pebbles within the urn. This problem was known as the ''inverse probability'' problem, and was a topic of res ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |