|
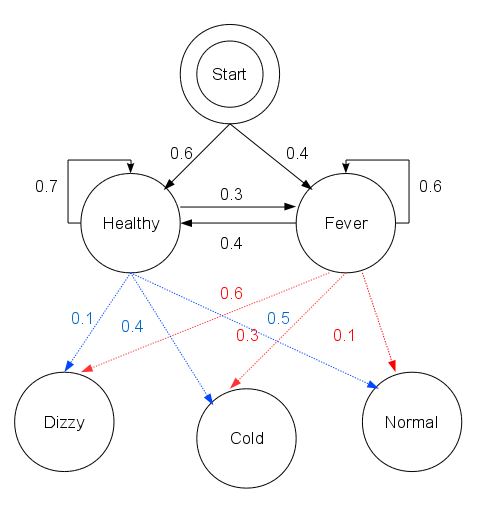
Hidden Markov Models
A hidden Markov model (HMM) is a Markov model in which the observations are dependent on a latent (or ''hidden'') Markov process (referred to as X). An HMM requires that there be an observable process Y whose outcomes depend on the outcomes of X in a known way. Since X cannot be observed directly, the goal is to learn about state of X by observing Y. By definition of being a Markov model, an HMM has an additional requirement that the outcome of Y at time t = t_0 must be "influenced" exclusively by the outcome of X at t = t_0 and that the outcomes of X and Y at t < t_0 must be conditionally independent of at given at time . Estimation of the parameters in an HMM can be performed using . For linear chain HMMs, the [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Markov Model
In probability theory, a Markov model is a stochastic model used to Mathematical model, model pseudo-randomly changing systems. It is assumed that future states depend only on the current state, not on the events that occurred before it (that is, it assumes the Markov property). Generally, this assumption enables reasoning and computation with the model that would otherwise be Intractability (complexity), intractable. For this reason, in the fields of predictive modelling and probabilistic forecasting, it is desirable for a given model to exhibit the Markov property. Introduction Andrey Andreyevich Markov (14 June 1856 – 20 July 1922) was a Russian mathematician best known for his work on stochastic processes. A primary subject of his research later became known as the Markov chain. There are four common Markov models used in different situations, depending on whether every sequential state is observable or not, and whether the system is to be adjusted on the basis of observation ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Partial Discharge
In electrical engineering, partial discharge (PD) is a localized dielectric breakdown (DB) (which does not completely bridge the space between the two conductors) of a small portion of a solid or fluid electrical insulation (EI) system under high voltage (HV) stress. While a corona discharge (CD) is usually revealed by a relatively steady glow or brush discharge (BD) in air, partial discharges within solid insulation system are not visible. PD can occur in a gaseous, liquid, or solid insulating medium. It often starts within gas voids, such as voids in solid epoxy insulation or bubbles in transformer oil. Protracted partial discharge can erode solid insulation and eventually lead to breakdown of insulation. Discharge mechanism PD usually begins within voids, cracks, or inclusions within a solid dielectric, at conductor-dielectric interfaces within solid or liquid dielectrics, or in bubbles within liquid dielectrics. Since PDs are limited to only a portion of the insulati ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Markov Property
In probability theory and statistics, the term Markov property refers to the memoryless property of a stochastic process, which means that its future evolution is independent of its history. It is named after the Russian mathematician Andrey Markov. The term strong Markov property is similar to the Markov property, except that the meaning of "present" is defined in terms of a random variable known as a stopping time. The term Markov assumption is used to describe a model where the Markov property is assumed to hold, such as a hidden Markov model. A Markov random field extends this property to two or more dimensions or to random variables defined for an interconnected network of items. An example of a model for such a field is the Ising model. A discrete-time stochastic process satisfying the Markov property is known as a Markov chain. Introduction A stochastic process has the Markov property if the conditional probability distribution of future states of the process (cond ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Conditional Probability Distribution
In probability theory and statistics, the conditional probability distribution is a probability distribution that describes the probability of an outcome given the occurrence of a particular event. Given two jointly distributed random variables X and Y, the conditional probability distribution of Y given X is the probability distribution of Y when X is known to be a particular value; in some cases the conditional probabilities may be expressed as functions containing the unspecified value x of X as a parameter. When both X and Y are categorical variables, a conditional probability table is typically used to represent the conditional probability. The conditional distribution contrasts with the marginal distribution of a random variable, which is its distribution without reference to the value of the other variable. If the conditional distribution of Y given X is a continuous distribution, then its probability density function is known as the conditional density function. The prop ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Trellis (graph)
A trellis is a graph whose nodes are ordered into vertical slices (''time'') with every node at almost every time connected to at least one node at an earlier and at least one node at a later time. The earliest and latest times in the trellis have only one node (hence the "almost" in the preceding sentence). Trellises are used in encoders and decoders for communication theory and encryption. They are also the central datatype used in Baum–Welch algorithm or the Viterbi AlgorithmRyan, M. S., & Nudd, G. R. (1993). The viterbi algorithm. University of Warwick, Department of Computer Science. for Hidden Markov Models. The trellis graph is named for its similar appearance to an architectural trellis. References See also * Trellis modulation Trellis coded modulation (TCM) is a modulation scheme that transmits information with high efficiency over band-limited channels such as telephone lines. Gottfried Ungerboeck invented trellis modulation while working for IBM in the 1970 ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Viterbi Algorithm
The Viterbi algorithm is a dynamic programming algorithm for obtaining the maximum a posteriori probability estimate of the most likely sequence of hidden states—called the Viterbi path—that results in a sequence of observed events. This is done especially in the context of Markov information sources and hidden Markov models (HMM). The algorithm has found universal application in decoding the convolutional codes used in both CDMA and GSM digital cellular, dial-up modems, satellite, deep-space communications, and 802.11 wireless LANs. It is now also commonly used in speech recognition, speech synthesis, diarization, keyword spotting, computational linguistics, and bioinformatics. For example, in speech-to-text (speech recognition), the acoustic signal is treated as the observed sequence of events, and a string of text is considered to be the "hidden cause" of the acoustic signal. The Viterbi algorithm finds the most likely string of text given the acoustic signal. His ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Python Programming Language
Python is a high-level, general-purpose programming language. Its design philosophy emphasizes code readability with the use of significant indentation. Python is dynamically type-checked and garbage-collected. It supports multiple programming paradigms, including structured (particularly procedural), object-oriented and functional programming. It is often described as a "batteries included" language due to its comprehensive standard library. Guido van Rossum began working on Python in the late 1980s as a successor to the ABC programming language, and he first released it in 1991 as Python 0.9.0. Python 2.0 was released in 2000. Python 3.0, released in 2008, was a major revision not completely backward-compatible with earlier versions. Python 2.7.18, released in 2020, was the last release of Python 2. Python consistently ranks as one of the most popular programming languages, and it has gained widespread use in the machine learning commu ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Markov Chain
In probability theory and statistics, a Markov chain or Markov process is a stochastic process describing a sequence of possible events in which the probability of each event depends only on the state attained in the previous event. Informally, this may be thought of as, "What happens next depends only on the state of affairs ''now''." A countably infinite sequence, in which the chain moves state at discrete time steps, gives a discrete-time Markov chain (DTMC). A continuous-time process is called a continuous-time Markov chain (CTMC). Markov processes are named in honor of the Russian mathematician Andrey Markov. Markov chains have many applications as statistical models of real-world processes. They provide the basis for general stochastic simulation methods known as Markov chain Monte Carlo, which are used for simulating sampling from complex probability distributions, and have found application in areas including Bayesian statistics, biology, chemistry, economics, fin ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Urn Problem
In probability and statistics, an urn problem is an idealized mental exercise in which some objects of real interest (such as atoms, people, cars, etc.) are represented as colored balls in an urn or other container. One pretends to remove one or more balls from the urn; the goal is to determine the probability of drawing one color or another, or some other properties. A number of important variations are described below. An urn model is either a set of probabilities that describe events within an urn problem, or it is a probability distribution, or a family of such distributions, of random variables associated with urn problems. History In ''Ars Conjectandi'' (1713), Jacob Bernoulli considered the problem of determining, given a number of pebbles drawn from an urn, the proportions of different colored pebbles within the urn. This problem was known as the ''inverse probability'' problem, and was a topic of research in the eighteenth century, attracting the attention of Abraham ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Borel Set
In mathematics, a Borel set is any subset of a topological space that can be formed from its open sets (or, equivalently, from closed sets) through the operations of countable union, countable intersection, and relative complement. Borel sets are named after Émile Borel. For a topological space ''X'', the collection of all Borel sets on ''X'' forms a σ-algebra, known as the Borel algebra or Borel σ-algebra. The Borel algebra on ''X'' is the smallest σ-algebra containing all open sets (or, equivalently, all closed sets). Borel sets are important in measure theory, since any measure defined on the open sets of a space, or on the closed sets of a space, must also be defined on all Borel sets of that space. Any measure defined on the Borel sets is called a Borel measure. Borel sets and the associated Borel hierarchy also play a fundamental role in descriptive set theory. In some contexts, Borel sets are defined to be generated by the compact sets of the topol ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |