|
Hyperbolic Domains 732c
Hyperbolic is an adjective describing something that resembles or pertains to a hyperbola (a curve), to hyperbole (an overstatement or exaggeration), or to hyperbolic geometry. The following phenomena are described as ''hyperbolic'' because they manifest hyperbolas, not because something about them is exaggerated. * Hyperbolic angle, an unbounded variable referring to a hyperbola instead of a circle * Hyperbolic coordinates, location by geometric mean and hyperbolic angle in quadrant I *Hyperbolic distribution, a probability distribution characterized by the logarithm of the probability density function being a hyperbola * Hyperbolic equilibrium point, a fixed point that does not have any center manifolds * Hyperbolic function, an analog of an ordinary trigonometric or circular function * Hyperbolic geometric graph, a random network generated by connecting nearby points sprinkled in a hyperbolic space * Hyperbolic geometry, a non-Euclidean geometry * Hyperbolic group, a finitely ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Hyperbola
In mathematics, a hyperbola (; pl. hyperbolas or hyperbolae ; adj. hyperbolic ) is a type of smooth curve lying in a plane, defined by its geometric properties or by equations for which it is the solution set. A hyperbola has two pieces, called connected components or branches, that are mirror images of each other and resemble two infinite bows. The hyperbola is one of the three kinds of conic section, formed by the intersection of a plane and a double cone. (The other conic sections are the parabola and the ellipse. A circle is a special case of an ellipse.) If the plane intersects both halves of the double cone but does not pass through the apex of the cones, then the conic is a hyperbola. Hyperbolas arise in many ways: * as the curve representing the reciprocal function y(x) = 1/x in the Cartesian plane, * as the path followed by the shadow of the tip of a sundial, * as the shape of an open orbit (as distinct from a closed elliptical orbit), such as the orbit of a s ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Split-complex Number
In algebra, a split complex number (or hyperbolic number, also perplex number, double number) has two real number components and , and is written z=x+yj, where j^2=1. The ''conjugate'' of is z^*=x-yj. Since j^2=1, the product of a number with its conjugate is N(z) := zz^* = x^2 - y^2, an isotropic quadratic form. The collection of all split complex numbers z=x+yj for forms an algebra over the field of real numbers. Two split-complex numbers and have a product that satisfies N(wz)=N(w)N(z). This composition of over the algebra product makes a composition algebra. A similar algebra based on and component-wise operations of addition and multiplication, where is the quadratic form on also forms a quadratic space. The ring isomorphism \begin D &\to \mathbb^2 \\ x + yj &\mapsto (x - y, x + y) \end relates proportional quadratic forms, but the mapping is an isometry since the multiplicative identity of is at a distance from 0, which is normalized in . S ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Exaggeration
Exaggeration is the representation of something as more extreme or dramatic than it really is. Exaggeration may occur intentionally or unintentionally. Exaggeration can be a rhetorical device or figure of speech. It may be used to evoke strong feelings or to create a strong impression. Amplifying achievements, obstacles and problems to seek attention is an everyday occurrence Inflating the difficulty of achieving a goal after attaining it, can be used to bolster self-esteem. In the arts, exaggerations are used to create emphasis or effect. As a literary device, exaggerations is often used in poetry, and is frequently encountered in casual speech. Many times the usages of hyperbole describes something as better or worse than it really is. An example of hyperbole is: "The bag weighed a ton." Hyperbole makes the point that the bag was very heavy, though it probably does not weigh a ton. Exaggerating is also a type of deception,Guerrero, L., Anderson, P., Afifi, W. (2007) ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Hyperbolic Versor
In mathematics, a versor is a quaternion of norm one (a ''unit quaternion''). The word is derived from Latin ''versare'' = "to turn" with the suffix ''-or'' forming a noun from the verb (i.e. ''versor'' = "the turner"). It was introduced by William Rowan Hamilton in the context of his quaternion theory. Each versor has the form :q = \exp(a\mathbf) = \cos a + \mathbf \sin a, \quad \mathbf^2 = -1, \quad a \in ,\pi where the r2 = −1 condition means that r is a unit-length vector quaternion (or that the first component of r is zero, and the last three components of r are a unit vector in 3 dimensions). The corresponding 3-dimensional rotation has the angle 2''a'' about the axis r in axis–angle representation. In case (a right angle), then q = \mathbf, and the resulting unit vector is termed a ''right versor''. Presentation on 3- and 2-spheres Hamilton denoted the versor of a quaternion ''q'' by the symbol U''q''. He was then able to display the general quaternion in polar coo ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Hyperbolic Trajectory
In astrodynamics or celestial mechanics, a hyperbolic trajectory or hyperbolic orbit is the trajectory of any object around a central body with more than enough speed to escape the central object's gravitational pull. The name derives from the fact that according to Newtonian theory such an orbit has the shape of a hyperbola. In more technical terms this can be expressed by the condition that the orbital eccentricity is greater than one. Under simplistic assumptions a body traveling along this trajectory will coast towards infinity, settling to a final excess velocity relative to the central body. Similarly to parabolic trajectories, all hyperbolic trajectories are also escape trajectories. The specific energy of a hyperbolic trajectory orbit is positive. Planetary flybys, used for gravitational slingshots, can be described within the planet's sphere of influence using hyperbolic trajectories. Parameters describing a hyperbolic trajectory Like an elliptical orbit, a hyperbol ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Hyperbolic Space
In mathematics, hyperbolic space of dimension n is the unique simply connected, n-dimensional Riemannian manifold of constant sectional curvature equal to -1. It is homogeneous, and satisfies the stronger property of being a symmetric space. There are many ways to construct it as an open subset of \mathbb R^n with an explicitly written Riemannian metric; such constructions are referred to as models. Hyperbolic 2-space, H2, which was the first instance studied, is also called the hyperbolic plane. It is also sometimes referred to as Lobachevsky space or Bolyai–Lobachevsky space after the names of the author who first published on the topic of hyperbolic geometry. Sometimes the qualificative "real" is added to differentiate it from complex hyperbolic spaces, quaternionic hyperbolic spaces and the octononic hyperbolic plane which are the other symmetric spaces of negative curvature. Hyperbolic space serves as the prototype of a Gromov hyperbolic space which is a far-reachin ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Hyperbolic Soccerball
In geometry, the order-7 truncated triangular tiling, sometimes called the hyperbolic soccerball, is a semiregular tiling of the hyperbolic plane. There are two hexagons and one heptagon on each vertex, forming a pattern similar to a conventional soccer ball (truncated icosahedron) with heptagons in place of pentagons. It has Schläfli symbol of t. Hyperbolic soccerball (football) This tiling is called a hyperbolic soccerball (football) for its similarity to the truncated icosahedron pattern used on soccer balls. Small portions of it as a hyperbolic surface can be constructed in 3-space. Dual tiling The dual tiling is called a ''heptakis heptagonal tiling'', named for being constructible as a heptagonal tiling with every heptagon divided into seven triangles by the center point. : Related tilings This hyperbolic tiling is topologically related as a part of sequence of uniform truncated polyhedra with vertex configurations (n.6.6), and ,3Coxeter group symmetry. From ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Hyperbolic Sector
A hyperbolic sector is a region of the Cartesian plane bounded by a hyperbola and two rays from the origin to it. For example, the two points and on the rectangular hyperbola , or the corresponding region when this hyperbola is re-scaled and its orientation is altered by a rotation leaving the center at the origin, as with the unit hyperbola. A hyperbolic sector in standard position has and . Hyperbolic sectors are the basis for the hyperbolic functions. Area The area of a hyperbolic sector in standard position is natural logarithm of ''b'' . Proof: Integrate under 1/''x'' from 1 to ''b'', add triangle , and subtract triangle . When in standard position, a hyperbolic sector corresponds to a positive hyperbolic angle at the origin, with the measure of the latter being defined as the area of the former. Hyperbolic triangle When in standard position, a hyperbolic sector determines a hyperbolic triangle, the right triangle with one vertex at the origin, base on the diag ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Squeeze Mapping
In linear algebra, a squeeze mapping, also called a squeeze transformation, is a type of linear map that preserves Euclidean area of regions in the Cartesian plane, but is ''not'' a rotation or shear mapping. For a fixed positive real number , the mapping :(x, y) \mapsto (ax, y/a) is the ''squeeze mapping'' with parameter . Since :\ is a hyperbola, if and , then and the points of the image of the squeeze mapping are on the same hyperbola as is. For this reason it is natural to think of the squeeze mapping as a hyperbolic rotation, as did Émile Borel in 1914, by analogy with ''circular rotations'', which preserve circles. Logarithm and hyperbolic angle The squeeze mapping sets the stage for development of the concept of logarithms. The problem of finding the area bounded by a hyperbola (such as is one of quadrature. The solution, found by Grégoire de Saint-Vincent and Alphonse Antonio de Sarasa in 1647, required the natural logarithm function, a new concept. Some insight ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Hyperbolic Quaternion
In abstract algebra, the algebra of hyperbolic quaternions is a nonassociative algebra over the real numbers with elements of the form :q = a + bi + cj + dk, \quad a,b,c,d \in \mathbb \! where the squares of i, j, and k are +1 and distinct elements of multiply with the anti-commutative property. The four-dimensional algebra of hyperbolic quaternions incorporates some of the features of the older and larger algebra of biquaternions. They both contain subalgebras isomorphic to the split-complex number plane. Furthermore, just as the quaternion algebra H can be viewed as a union of complex planes, so the hyperbolic quaternion algebra is a union of split-complex number planes sharing the same real line. It was Alexander Macfarlane who promoted this concept in the 1890s as his ''Algebra of Physics'', first through the American Association for the Advancement of Science in 1891, then through his 1894 book of five ''Papers in Space Analysis'', and in a series of lectures at Lehig ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
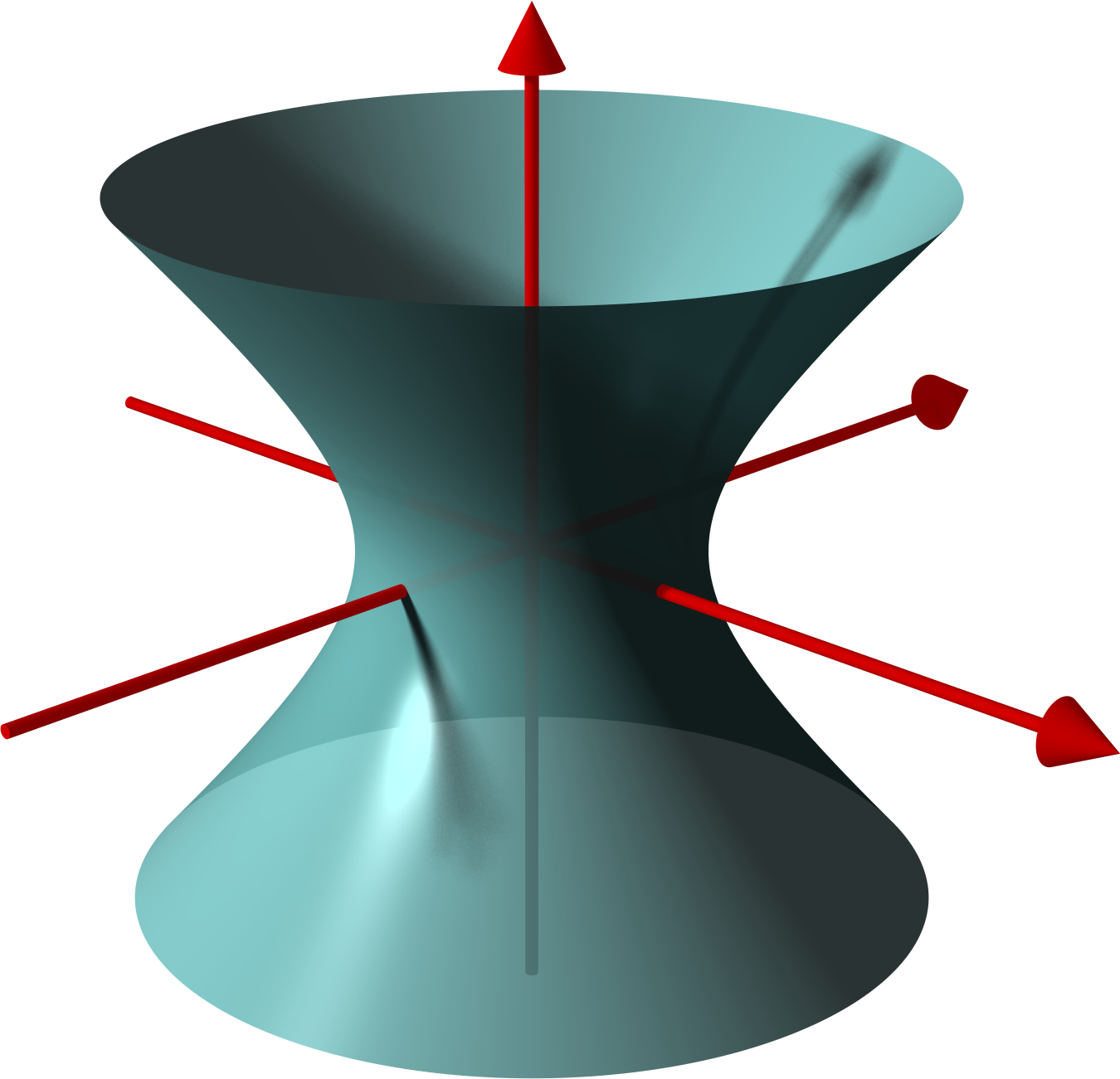
Hyperboloid
In geometry, a hyperboloid of revolution, sometimes called a circular hyperboloid, is the surface generated by rotating a hyperbola around one of its principal axes. A hyperboloid is the surface obtained from a hyperboloid of revolution by deforming it by means of directional scalings, or more generally, of an affine transformation. A hyperboloid is a quadric surface, that is, a surface defined as the zero set of a polynomial of degree two in three variables. Among quadric surfaces, a hyperboloid is characterized by not being a cone or a cylinder, having a center of symmetry, and intersecting many planes into hyperbolas. A hyperboloid has three pairwise perpendicular axes of symmetry, and three pairwise perpendicular planes of symmetry. Given a hyperboloid, one can choose a Cartesian coordinate system such that the hyperboloid is defined by one of the following equations: : + - = 1, or : + - = -1. The coordinate axes are axes of symmetry of the hyperboloid and the ori ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Isotropic Quadratic Form
In mathematics, a quadratic form over a field ''F'' is said to be isotropic if there is a non-zero vector on which the form evaluates to zero. Otherwise the quadratic form is anisotropic. More precisely, if ''q'' is a quadratic form on a vector space ''V'' over ''F'', then a non-zero vector ''v'' in ''V'' is said to be isotropic if . A quadratic form is isotropic if and only if there exists a non-zero isotropic vector (or null vector) for that quadratic form. Suppose that is quadratic space and ''W'' is a subspace of ''V''. Then ''W'' is called an isotropic subspace of ''V'' if ''some'' vector in it is isotropic, a totally isotropic subspace if ''all'' vectors in it are isotropic, and an anisotropic subspace if it does not contain ''any'' (non-zero) isotropic vectors. The of a quadratic space is the maximum of the dimensions of the totally isotropic subspaces. A quadratic form ''q'' on a finite-dimensional real vector space ''V'' is anisotropic if and only if ''q'' is a defin ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |