|
Huffman Code
In computer science and information theory, a Huffman code is a particular type of optimal prefix code that is commonly used for lossless data compression. The process of finding or using such a code proceeds by means of Huffman coding, an algorithm developed by David A. Huffman while he was a Sc.D. student at MIT, and published in the 1952 paper "A Method for the Construction of Minimum-Redundancy Codes". The output from Huffman's algorithm can be viewed as a variable-length code table for encoding a source symbol (such as a character in a file). The algorithm derives this table from the estimated probability or frequency of occurrence (''weight'') for each possible value of the source symbol. As in other entropy encoding methods, more common symbols are generally represented using fewer bits than less common symbols. Huffman's method can be efficiently implemented, finding a code in time linear to the number of input weights if these weights are sorted. However, although o ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
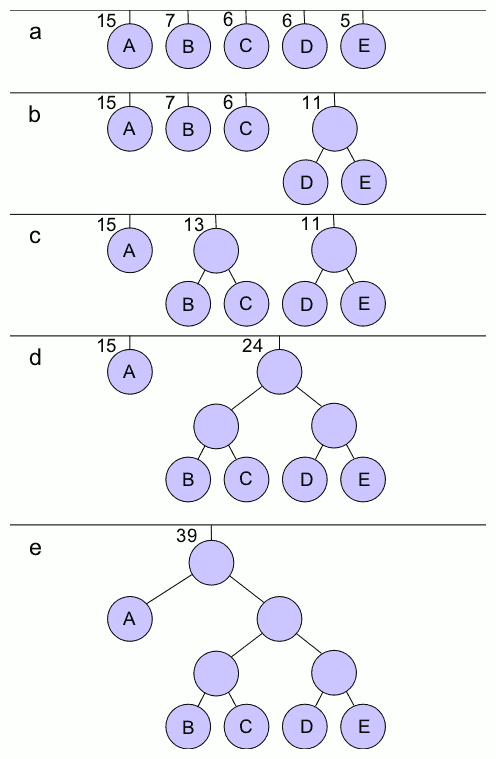
Huffman Tree 2
Huffman may refer to: __NOTOC__ Places United States * Huffman, Indiana, an unincorporated community * Huffman, Texas, an unincorporated community * Huffman, Virginia, an unincorporated community * Huffman, West Virginia, an unincorporated community Antarctica * Mount Huffman, Ellsworth Land People * Huffman (surname), a surname * Huffman Eja-Tabe (born 1981), Cameroonian footballer in North America Other uses * Huffman Bros. Motor Co, 1920s Indiana-based car company * Huffman High School, Birmingham, Alabama * Huffman Manufacturing Company, former name of the Huffy Corporation, a bicycle manufacturer based in Dayton, Ohio See also * Huffman coding, a data compression algorithm (''Huffman tree'') by David A. Huffman * Huffman Dam, near Fairborn, Ohio * Huffman Historic District, Dayton, Ohio, on the National Register of Historic Places * Huffman Prairie, Ohio, also known as Huffman Field, a field used by the Wright brothers for testing and training *Hoffman (disambiguation ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Term Paper
A term paper is a research paper written by students over an academic term, accounting for a large part of a grade. Merriam-Webster defines it as "a major written assignment in a school or college course representative of a student's achievement during a term". Term papers are generally intended to describe an event, a concept, or argue a point. It is a written original work discussing a topic in detail, usually several typed pages in length, and is often due at the end of a semester. There is much overlap between the terms: ''research paper'' and ''term paper''. A ''term paper'' was originally a written assignment (usually a research based paper) that was due at the end of the "term"—either a semester or quarter, depending on which unit of measure a school used. However, not all term papers involve academic research, and not all research papers are term papers. History Term papers date back to the beginning of the 19th century when print could be reproduced cheaply and written ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Information Entropy
In information theory, the entropy of a random variable is the average level of "information", "surprise", or "uncertainty" inherent to the variable's possible outcomes. Given a discrete random variable X, which takes values in the alphabet \mathcal and is distributed according to p: \mathcal\to, 1/math>: \Eta(X) := -\sum_ p(x) \log p(x) = \mathbb \log p(X), where \Sigma denotes the sum over the variable's possible values. The choice of base for \log, the logarithm, varies for different applications. Base 2 gives the unit of bits (or " shannons"), while base ''e'' gives "natural units" nat, and base 10 gives units of "dits", "bans", or " hartleys". An equivalent definition of entropy is the expected value of the self-information of a variable. The concept of information entropy was introduced by Claude Shannon in his 1948 paper " A Mathematical Theory of Communication",PDF archived froherePDF archived frohere and is also referred to as Shannon entropy. Shannon's theory ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
A Mathematical Theory Of Communication
"A Mathematical Theory of Communication" is an article by mathematician Claude E. Shannon published in '' Bell System Technical Journal'' in 1948. It was renamed ''The Mathematical Theory of Communication'' in the 1949 book of the same name, a small but significant title change after realizing the generality of this work. It became one of the most cited scientific articles and gave rise to the field of information theory. Publication The article was the founding work of the field of information theory. It was later published in 1949 as a book titled ''The Mathematical Theory of Communication'' (), which was published as a paperback in 1963 (). The book contains an additional article by Warren Weaver, providing an overview of the theory for a more general audience. Contents Shannon's article laid out the basic elements of communication: *An information source that produces a message *A transmitter that operates on the message to create a signal which can be sent through a channel ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Variable-length Code
In coding theory a variable-length code is a code which maps source symbols to a ''variable'' number of bits. Variable-length codes can allow sources to be compressed and decompressed with ''zero'' error (lossless data compression) and still be read back symbol by symbol. With the right coding strategy an independent and identically-distributed source may be compressed almost arbitrarily close to its entropy. This is in contrast to fixed length coding methods, for which data compression is only possible for large blocks of data, and any compression beyond the logarithm of the total number of possibilities comes with a finite (though perhaps arbitrarily small) probability of failure. Some examples of well-known variable-length coding strategies are Huffman coding, Lempel–Ziv coding, arithmetic coding, and context-adaptive variable-length coding. Codes and their extensions The extension of a code is the mapping of finite length source sequences to finite length bit stri ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Shannon Entropy
Shannon may refer to: People * Shannon (given name) * Shannon (surname) * Shannon (American singer), stage name of singer Shannon Brenda Greene (born 1958) * Shannon (South Korean singer), British-South Korean singer and actress Shannon Arrum Williams (born 1998) * Shannon, intermittent stage name of English singer-songwriter Marty Wilde (born 1939) * Claude Shannon (1916-2001) was American mathematician, electrical engineer, and cryptographer known as a "father of information theory" Places Australia * Shannon, Tasmania, a locality * Hundred of Shannon, a cadastral unit in South Australia * Shannon, a former name for the area named Calomba, South Australia since 1916 * Shannon River (Western Australia) Canada * Shannon, New Brunswick, a community * Shannon, Quebec, a city * Shannon Bay, former name of Darrell Bay, British Columbia * Shannon Falls, a waterfall in British Columbia Ireland * River Shannon, the longest river in Ireland ** Shannon Cave, a subterranean section ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Weighted Path Length From The Root
A weight function is a mathematical device used when performing a sum, integral, or average to give some elements more "weight" or influence on the result than other elements in the same set. The result of this application of a weight function is a weighted sum or weighted average. Weight functions occur frequently in statistics and analysis, and are closely related to the concept of a measure. Weight functions can be employed in both discrete and continuous settings. They can be used to construct systems of calculus called "weighted calculus" and "meta-calculus".Jane Grossma''Meta-Calculus: Differential and Integral'' , 1981. Discrete weights General definition In the discrete setting, a weight function w \colon A \to \R^+ is a positive function defined on a discrete set A, which is typically finite or countable. The weight function w(a) := 1 corresponds to the ''unweighted'' situation in which all elements have equal weight. One can then apply this weight to various con ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Expected Value
In probability theory, the expected value (also called expectation, expectancy, mathematical expectation, mean, average, or first moment) is a generalization of the weighted average. Informally, the expected value is the arithmetic mean of a large number of independently selected outcomes of a random variable. The expected value of a random variable with a finite number of outcomes is a weighted average of all possible outcomes. In the case of a continuum of possible outcomes, the expectation is defined by integration. In the axiomatic foundation for probability provided by measure theory, the expectation is given by Lebesgue integration. The expected value of a random variable is often denoted by , , or , with also often stylized as or \mathbb. History The idea of the expected value originated in the middle of the 17th century from the study of the so-called problem of points, which seeks to divide the stakes ''in a fair way'' between two players, who have to e ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Prefix Code
A prefix code is a type of code system distinguished by its possession of the "prefix property", which requires that there is no whole code word in the system that is a prefix (computer science), prefix (initial segment) of any other code word in the system. It is trivially true for fixed-length code, so only a point of consideration in variable-length code. For example, a code with code words has the prefix property; a code consisting of does not, because "5" is a prefix of "59" and also of "55". A prefix code is a uniquely decodable code: given a complete and accurate sequence, a receiver can identify each word without requiring a special marker between words. However, there are uniquely decodable codes that are not prefix codes; for instance, the reverse of a prefix code is still uniquely decodable (it is a suffix code), but it is not necessarily a prefix code. Prefix codes are also known as prefix-free codes, prefix condition codes and instantaneous codes. Although Huffman cod ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Proportionality (mathematics)
In mathematics, two sequences of numbers, often experimental data, are proportional or directly proportional if their corresponding elements have a constant ratio, which is called the coefficient of proportionality or proportionality constant. Two sequences are inversely proportional if corresponding elements have a constant product, also called the coefficient of proportionality. This definition is commonly extended to related varying quantities, which are often called ''variables''. This meaning of ''variable'' is not the common meaning of the term in mathematics (see variable (mathematics)); these two different concepts share the same name for historical reasons. Two functions f(x) and g(x) are ''proportional'' if their ratio \frac is a constant function. If several pairs of variables share the same direct proportionality constant, the equation expressing the equality of these ratios is called a proportion, e.g., (for details see Ratio). Proportionality is closely r ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Shannon–Fano Coding
In the field of data compression, Shannon–Fano coding, named after Claude Shannon and Robert Fano, is a name given to two different but related techniques for constructing a prefix code based on a set of symbols and their probabilities (estimated or measured). * Shannon's method chooses a prefix code where a source symbol i is given the codeword length l_i = \lceil - \log_2 p_i\rceil. One common way of choosing the codewords uses the binary expansion of the cumulative probabilities. This method was proposed in Shannon's "A Mathematical Theory of Communication" (1948), his article introducing the field of information theory. * Fano's method divides the source symbols into two sets ("0" and "1") with probabilities as close to 1/2 as possible. Then those sets are themselves divided in two, and so on, until each set contains only one symbol. The codeword for that symbol is the string of "0"s and "1"s that records which half of the divides it fell on. This method was proposed in a l ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |