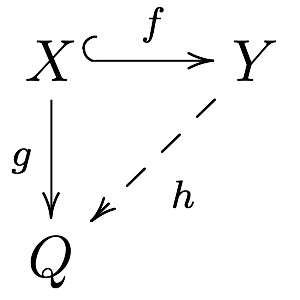|
Horseshoe Lemma
In homological algebra, the horseshoe lemma, also called the simultaneous resolution theorem, is a statement relating resolutions of two objects A' and A'' to resolutions of extensions of A' by A''. It says that if an object A is an extension of A' by A'', then a resolution of A can be built up inductively with the ''n''th item in the resolution equal to the coproduct of the ''n''th items in the resolutions of A' and A''. The name of the lemma comes from the shape of the diagram illustrating the lemma's hypothesis. Formal statement Let \mathcal be an abelian category with enough projectives. If is a diagram in \mathcal such that the column is exact and the rows are projective resolutions of A' and A'' respectively, then it can be completed to a commutative diagram where all columns are exact, the middle row is a projective resolution of A, and P_n=P'_n\oplus P''_n for all ''n''. If \mathcal is an abelian category with enough injectives, the dual statement also holds. The ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Homological Algebra
Homological algebra is the branch of mathematics that studies homology (mathematics), homology in a general algebraic setting. It is a relatively young discipline, whose origins can be traced to investigations in combinatorial topology (a precursor to algebraic topology) and abstract algebra (theory of module (mathematics), modules and Syzygy (mathematics), syzygies) at the end of the 19th century, chiefly by Henri Poincaré and David Hilbert. Homological algebra is the study of homological functors and the intricate algebraic structures that they entail; its development was closely intertwined with the emergence of category theory. A central concept is that of chain complexes, which can be studied through both their homology and cohomology. Homological algebra affords the means to extract information contained in these complexes and present it in the form of homological invariant (mathematics), invariants of ring (mathematics), rings, modules, topological spaces, and other 'tan ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Projective Resolution
In mathematics, and more specifically in homological algebra, a resolution (or left resolution; dually a coresolution or right resolution) is an exact sequence of modules (or, more generally, of objects of an abelian category), which is used to define invariants characterizing the structure of a specific module or object of this category. When, as usually, arrows are oriented to the right, the sequence is supposed to be infinite to the left for (left) resolutions, and to the right for right resolutions. However, a finite resolution is one where only finitely many of the objects in the sequence are non-zero; it is usually represented by a finite exact sequence in which the leftmost object (for resolutions) or the rightmost object (for coresolutions) is the zero-object. Generally, the objects in the sequence are restricted to have some property ''P'' (for example to be free). Thus one speaks of a ''P resolution''. In particular, every module has free resolutions, projective resolut ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mathematical Induction
Mathematical induction is a method for proving that a statement ''P''(''n'') is true for every natural number ''n'', that is, that the infinitely many cases ''P''(0), ''P''(1), ''P''(2), ''P''(3), ... all hold. Informal metaphors help to explain this technique, such as falling dominoes or climbing a ladder: A proof by induction consists of two cases. The first, the base case, proves the statement for ''n'' = 0 without assuming any knowledge of other cases. The second case, the induction step, proves that ''if'' the statement holds for any given case ''n'' = ''k'', ''then'' it must also hold for the next case ''n'' = ''k'' + 1. These two steps establish that the statement holds for every natural number ''n''. The base case does not necessarily begin with ''n'' = 0, but often with ''n'' = 1, and possibly with any fixed natural number ''n'' = ''N'', establishing the truth of the statement for all natu ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Coproduct
In category theory, the coproduct, or categorical sum, is a construction which includes as examples the disjoint union of sets and of topological spaces, the free product of groups, and the direct sum of modules and vector spaces. The coproduct of a family of objects is essentially the "least specific" object to which each object in the family admits a morphism. It is the category-theoretic dual notion to the categorical product, which means the definition is the same as the product but with all arrows reversed. Despite this seemingly innocuous change in the name and notation, coproducts can be and typically are dramatically different from products. Definition Let C be a category and let X_1 and X_2 be objects of C. An object is called the coproduct of X_1 and X_2, written X_1 \sqcup X_2, or X_1 \oplus X_2, or sometimes simply X_1 + X_2, if there exist morphisms i_1 : X_1 \to X_1 \sqcup X_2 and i_2 : X_2 \to X_1 \sqcup X_2 satisfying the following universal property: for ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Abelian Category
In mathematics, an abelian category is a category in which morphisms and objects can be added and in which kernels and cokernels exist and have desirable properties. The motivating prototypical example of an abelian category is the category of abelian groups, Ab. The theory originated in an effort to unify several cohomology theories by Alexander Grothendieck and independently in the slightly earlier work of David Buchsbaum. Abelian categories are very ''stable'' categories; for example they are regular and they satisfy the snake lemma. The class of abelian categories is closed under several categorical constructions, for example, the category of chain complexes of an abelian category, or the category of functors from a small category to an abelian category are abelian as well. These stability properties make them inevitable in homological algebra and beyond; the theory has major applications in algebraic geometry, cohomology and pure category theory. Abelian categories are na ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Projective Object
In category theory, the notion of a projective object generalizes the notion of a projective module. Projective objects in abelian categories are used in homological algebra. The dual notion of a projective object is that of an injective object. Definition An object P in a category \mathcal is ''projective'' if for any epimorphism e:E\twoheadrightarrow X and morphism f:P\to X, there is a morphism \overline:P\to E such that e\circ \overline=f, i.e. the following diagram commutes: That is, every morphism P\to X factors through every epimorphism E\twoheadrightarrow X. If ''C'' is locally small, i.e., in particular \operatorname_C(P, X) is a set for any object ''X'' in ''C'', this definition is equivalent to the condition that the hom functor (also known as corepresentable functor) : \operatorname(P,-)\colon\mathcal\to\mathbf preserves epimorphisms. Projective objects in abelian categories If the category ''C'' is an abelian category such as, for example, the category of abeli ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Horseshoe Lemma
In homological algebra, the horseshoe lemma, also called the simultaneous resolution theorem, is a statement relating resolutions of two objects A' and A'' to resolutions of extensions of A' by A''. It says that if an object A is an extension of A' by A'', then a resolution of A can be built up inductively with the ''n''th item in the resolution equal to the coproduct of the ''n''th items in the resolutions of A' and A''. The name of the lemma comes from the shape of the diagram illustrating the lemma's hypothesis. Formal statement Let \mathcal be an abelian category with enough projectives. If is a diagram in \mathcal such that the column is exact and the rows are projective resolutions of A' and A'' respectively, then it can be completed to a commutative diagram where all columns are exact, the middle row is a projective resolution of A, and P_n=P'_n\oplus P''_n for all ''n''. If \mathcal is an abelian category with enough injectives, the dual statement also holds. The ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Commutative Diagram
350px, The commutative diagram used in the proof of the five lemma. In mathematics, and especially in category theory, a commutative diagram is a diagram such that all directed paths in the diagram with the same start and endpoints lead to the same result. It is said that commutative diagrams play the role in category theory that equations play in algebra. Description A commutative diagram often consists of three parts: * objects (also known as ''vertices'') * morphisms (also known as ''arrows'' or ''edges'') * paths or composites Arrow symbols In algebra texts, the type of morphism can be denoted with different arrow usages: * A monomorphism may be labeled with a \hookrightarrow or a \rightarrowtail. * An epimorphism may be labeled with a \twoheadrightarrow. * An isomorphism may be labeled with a \overset. * The dashed arrow typically represents the claim that the indicated morphism exists (whenever the rest of the diagram holds); the arrow may be optionally labeled as \exist ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Exact Sequence
An exact sequence is a sequence of morphisms between objects (for example, groups, rings, modules, and, more generally, objects of an abelian category) such that the image of one morphism equals the kernel of the next. Definition In the context of group theory, a sequence :G_0\;\xrightarrow\; G_1 \;\xrightarrow\; G_2 \;\xrightarrow\; \cdots \;\xrightarrow\; G_n of groups and group homomorphisms is said to be exact at G_i if \operatorname(f_i)=\ker(f_). The sequence is called exact if it is exact at each G_i for all 1\leq i |
Horseshoe Lemma Conclusion
A horseshoe is a fabricated product designed to protect a horse hoof from wear. Shoes are attached on the palmar surface (ground side) of the hooves, usually nailed through the insensitive hoof wall that is anatomically akin to the human toenail, although much larger and thicker. However, there are also cases where shoes are glued. Horseshoes are available in a wide variety of materials and styles, developed for different types of horse and for the work they do. The most common materials are steel and aluminium, but specialized shoes may include use of rubber, plastic, magnesium, titanium, or copper.Price, Steven D. (ed.) ''The Whole Horse Catalog: Revised and Updated'' New York:Fireside 1998 , pp. 84–87. Steel tends to be preferred in sports in which a strong, long-wearing shoe is needed, such as polo, eventing, show jumping, and western riding events. Aluminium shoes are lighter, making them common in horse racing where a lighter shoe is desired, and often faci ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Injective Object
In mathematics, especially in the field of category theory, the concept of injective object is a generalization of the concept of injective module. This concept is important in cohomology, in homotopy theory and in the theory of model categories. The dual notion is that of a projective object. Definition An object Q in a category \mathbf is said to be injective if for every monomorphism f: X \to Y and every morphism g: X \to Q there exists a morphism h: Y \to Q extending g to Y, i.e. such that h \circ f = g. That is, every morphism X \to Q factors through every monomorphism X \hookrightarrow Y. The morphism h in the above definition is not required to be uniquely determined by f and g. In a locally small category, it is equivalent to require that the hom functor \operatorname_(-,Q) carries monomorphisms in \mathbf to surjective set maps. In Abelian categories The notion of injectivity was first formulated for abelian categories, and this is still one of its primary areas of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Opposite Category
In category theory, a branch of mathematics, the opposite category or dual category ''C''op of a given category ''C'' is formed by reversing the morphisms, i.e. interchanging the source and target of each morphism. Doing the reversal twice yields the original category, so the opposite of an opposite category is the original category itself. In symbols, (C^)^ = C. Examples * An example comes from reversing the direction of inequalities in a partial order. So if ''X'' is a set and ≤ a partial order relation, we can define a new partial order relation ≤op by :: ''x'' ≤op ''y'' if and only if ''y'' ≤ ''x''. : The new order is commonly called dual order of ≤, and is mostly denoted by ≥. Therefore, duality plays an important role in order theory and every purely order theoretic concept has a dual. For example, there are opposite pairs child/parent, descendant/ancestor, infimum/supremum, down-set/ up-set, ideal/filter etc. This order theoretic duality is in turn a special c ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |