|
Hooper's Paradox
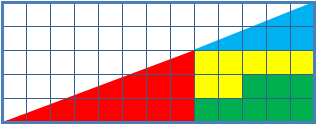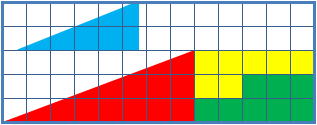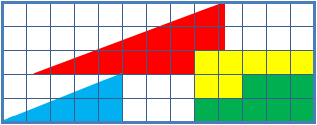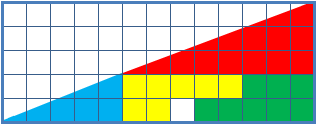
Hooper's paradox is a falsidical paradox based on an optical illusion. A geometric shape with an area of 32 units is dissected into four parts, which afterwards get assembled into a rectangle with an area of only 30 units. Explanation Upon close inspection one can notice that the triangles of the dissected shape are not identical to the triangles in the rectangle. The length of the shorter side at the right angle measures 2 units in the original shape but only 1.8 units in the rectangle. This means, the real triangles of the original shape overlap in the rectangle. The overlapping area is a parallelogram, the diagonals and sides of which can be computed via the Pythagorean theorem. : d_1=\sqrt=\sqrt : d_2=\sqrt=\sqrt : s_1=\sqrt=\sqrt : s_2=\sqrt=\sqrt The area of this parallelogram can determined using Heron's formula for triangles. This yields : s=\frac=\frac for the halved circumference of the triangle (half of the parallelogram) and with that for the area of the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Hooper Paradox
The word hooper is an archaic English term for a person who aided a cooper in the building of barrels by creating the hoop for the barrel. Hooper may also refer to: Place names in the United States: * Hooper, Colorado, town in Alamosa County, Colorado * Hooper, Georgia, an unincorporated community * Hooper, Nebraska, town in Dodge County, Nebraska * Hooper, Utah, place in Weber County, Utah * Hooper Bay, Alaska, town in Alaska * Hooper Township, Dodge County, Nebraska Other: * ''Hooper'' (film), 1978 comedy film starring Burt Reynolds * Hooper (mascot), the mascot for the National Basketball Association team, Detroit Pistons * Hooper (coachbuilder), a British coachbuilder fitting bodies to many Rolls-Royce and Daimler cars * USS ''Hooper'' (DE-1026), a destroyer escort in the US Navy * Hooper Ratings, an early audience measurement in early radio and television * Hooper, someone who practices dance form of Hooping People with the surname Hooper: * Hooper (surname) See also * ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Falsidical Paradox
A paradox is a logically self-contradictory statement or a statement that runs contrary to one's expectation. It is a statement that, despite apparently valid reasoning from true premises, leads to a seemingly self-contradictory or a logically unacceptable conclusion. A paradox usually involves contradictory-yet-interrelated elements that exist simultaneously and persist over time. They result in "persistent contradiction between interdependent elements" leading to a lasting "unity of opposites". In logic, many paradoxes exist that are known to be invalid arguments, yet are nevertheless valuable in promoting critical thinking, while other paradoxes have revealed errors in definitions that were assumed to be rigorous, and have caused axioms of mathematics and logic to be re-examined. One example is Russell's paradox, which questions whether a "list of all lists that do not contain themselves" would include itself, and showed that attempts to found set theory on the identificatio ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Hooper Paradox Explanation
The word hooper is an archaic English term for a person who aided a cooper in the building of barrels by creating the hoop for the barrel. Hooper may also refer to: Place names in the United States: * Hooper, Colorado, town in Alamosa County, Colorado * Hooper, Georgia, an unincorporated community * Hooper, Nebraska, town in Dodge County, Nebraska * Hooper, Utah, place in Weber County, Utah * Hooper Bay, Alaska, town in Alaska * Hooper Township, Dodge County, Nebraska Other: * ''Hooper'' (film), 1978 comedy film starring Burt Reynolds * Hooper (mascot), the mascot for the National Basketball Association team, Detroit Pistons * Hooper (coachbuilder), a British coachbuilder fitting bodies to many Rolls-Royce and Daimler cars * USS ''Hooper'' (DE-1026), a destroyer escort in the US Navy * Hooper Ratings, an early audience measurement in early radio and television * Hooper, someone who practices dance form of Hooping People with the surname Hooper: * Hooper (surname) See also * ' ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Pythagorean Theorem
In mathematics, the Pythagorean theorem or Pythagoras' theorem is a fundamental relation in Euclidean geometry between the three sides of a right triangle. It states that the area of the square whose side is the hypotenuse (the side opposite the right angle) is equal to the sum of the areas of the squares on the other two sides. This theorem can be written as an equation relating the lengths of the sides ''a'', ''b'' and the hypotenuse ''c'', often called the Pythagorean equation: :a^2 + b^2 = c^2 , The theorem is named for the Greek philosopher Pythagoras, born around 570 BC. The theorem has been proven numerous times by many different methods – possibly the most for any mathematical theorem. The proofs are diverse, including both geometric proofs and algebraic proofs, with some dating back thousands of years. When Euclidean space is represented by a Cartesian coordinate system in analytic geometry, Euclidean distance satisfies the Pythagorean relation: the squared ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Heron's Formula
In geometry, Heron's formula (or Hero's formula) gives the area of a triangle in terms of the three side lengths , , . If s = \tfrac12(a + b + c) is the semiperimeter of the triangle, the area is, :A = \sqrt. It is named after first-century engineer Heron of Alexandria (or Hero) who proved it in his work ''Metrica'', though it was probably known centuries earlier. Example Let be the triangle with sides , and . This triangle’s semiperimeter is :s=\frac=\frac=16 and so the area is : \begin A &= \sqrt = \sqrt\\ &= \sqrt = \sqrt = 24. \end In this example, the side lengths and area are integers, making it a Heronian triangle. However, Heron's formula works equally well in cases where one or more of the side lengths are not integers. Alternate expressions Heron's formula can also be written in terms of just the side lengths instead of using the semiperimeter, in several ways, :\begin A &=\tfrac\sqrt \\ mu&=\tfrac\sqrt \\ mu&=\tfrac\sqrt \\ mu&=\tfrac\sqrt \\ mu&=\ ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Edmé-Gilles Guyot
Edmé-Gilles Guyot (1706–1786) was a French mail clerk, physician, postmaster, cartographer, inventor and author on the subject of mathematics, physics and magic. He experimented with optical illusions and with the theory behind performance magic. His developments into the apparent appearance of ghosts, using the projection of a figure into smoke, helped to create the technology and techniques used in phantasmagoria. Mathematics, science, and magic Manufacturer of conjuring apparatus and scientific instruments, Guyot was accused of exploiting and revealing the tricks used at the time by magicians and science populizers like Nicolas-Philippe Ledru and François Pelletier. He created "magic theatres" for the aristocracy – small boxes that use lanterns and slides to create an animated story. Guyot's work was influential in the development of magic lanterns and their use in phantasmagoria. In 1770 he detailed a method of simultaneously using two different slides in this early proje ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Chessboard Paradox
The chessboard paradoxGreg N. Frederickson: ''Dissections: Plane and Fancy''. Cambridge University Press, 2003, , chapter 23, pp. 268–277 in particular pp. 271–274 Colin Foster: "Slippery Slopes". In: ''Mathematics in School'', vol. 34, no. 3 (May, 2005), pp. 33–34JSTOR or paradox of Loyd and SchlömilchFranz Lemmermeyer: ''Mathematik à la Carte: Elementargeometrie an Quadratwurzeln mit einigen geschichtlichen Bemerkungen''. Springer 2014, , pp95–96(German) is a falsidical paradox based on an optical illusion. A chessboard or a square with a side length of 8 units is cut into four pieces. Those four pieces are used to form a rectangle with side lengths of 13 and 5 units. Hence the combined area of all four pieces is 64 area units in the square but 65 area units in the rectangle, this seeming contradiction is due an optical illusion as the four pieces don't fit exactly in the rectangle, but leave a small barely visible gap around the rectangle's diagonal. The paradox is ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Missing Square Puzzle
The missing square puzzle is an optical illusion used in mathematics classes to help students reason about geometrical figures; or rather to teach them not to reason using figures, but to use only textual descriptions and the axioms of geometry. It depicts two arrangements made of similar shapes in slightly different configurations. Each apparently forms a 13×5 right-angled triangle, but one has a 1×1 hole in it. Solution The key to the puzzle is the fact that neither of the 13×5 "triangles" is truly a triangle, nor would either truly be 13x5 if it were, because what appears to be the hypotenuse is bent. In other words, the "hypotenuse" does not maintain a consistent slope, even though it may appear that way to the human eye. A true 13×5 triangle cannot be created from the given component parts. The four figures (the yellow, red, blue and green shapes) total 32 units of area. The apparent triangles formed from the figures are 13 units wide and 5 units tall, so it appea ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Martin Gardner
Martin Gardner (October 21, 1914May 22, 2010) was an American popular mathematics and popular science writer with interests also encompassing scientific skepticism, micromagic, philosophy, religion, and literatureespecially the writings of Lewis Carroll, L. Frank Baum, and G. K. Chesterton.Martin (2010) He was also a leading authority on Lewis Carroll. '' The Annotated Alice'', which incorporated the text of Carroll's two Alice books, was his most successful work and sold over a million copies. He had a lifelong interest in magic and illusion and in 1999, MAGIC magazine named him as one of the "100 Most Influential Magicians of the Twentieth Century". He was considered the doyen of American puzzlers. He was a prolific and versatile author, publishing more than 100 books. Gardner was best known for creating and sustaining interest in recreational mathematicsand by extension, mathematics in generalthroughout the latter half of the 20th century, principally through his " ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Optical Illusions
Within visual perception, an optical illusion (also called a visual illusion) is an illusion caused by the visual system and characterized by a visual percept that arguably appears to differ from reality. Illusions come in a wide variety; their categorization is difficult because the underlying cause is often not clear but a classification proposed by Richard Gregory is useful as an orientation. According to that, there are three main classes: physical, physiological, and cognitive illusions, and in each class there are four kinds: Ambiguities, distortions, paradoxes, and fictions. A classical example for a physical distortion would be the apparent bending of a stick half immerged in water; an example for a physiological paradox is the motion aftereffect (where, despite movement, position remains unchanged). An example for a physiological fiction is an afterimage. Three typical cognitive distortions are the Ponzo, Poggendorff, and Müller-Lyer illusion. Physical illusions ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Elementary Mathematics
Elementary mathematics consists of mathematics topics frequently taught at the primary or secondary school levels. In the Canadian curriculum, there are six basic strands in Elementary Mathematics: Number, Algebra, Data, Spatial Sense, Financial Literacy, and Social emotional learning skills and math processes. These six strands are the focus of Mathematics education from grade 1 through grade 8. In secondary school, the main topics in elementary mathematics from grade nine until grade ten are: Number Sense and algebra, Linear Relations, Measurement and Geometry. Once students enter grade eleven and twelve students begin university and college preparation classes, which include: Functions, Calculus & Vectors, Advanced Functions, and Data Management. Strands of elementary mathematics Number Sense and Numeration Number Sense is an understanding of numbers and operations. In the 'Number Sense and Numeration' strand students develop an understanding of numbers by being taugh ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mathematical Paradoxes
Mathematics is an area of knowledge that includes the topics of numbers, formulas and related structures, shapes and the spaces in which they are contained, and quantities and their changes. These topics are represented in modern mathematics with the major subdisciplines of number theory, algebra, geometry, and analysis, respectively. There is no general consensus among mathematicians about a common definition for their academic discipline. Most mathematical activity involves the discovery of properties of abstract objects and the use of pure reason to prove them. These objects consist of either abstractions from nature orin modern mathematicsentities that are stipulated to have certain properties, called axioms. A ''proof'' consists of a succession of applications of deductive rules to already established results. These results include previously proved theorems, axioms, andin case of abstraction from naturesome basic properties that are considered true starting points of t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |