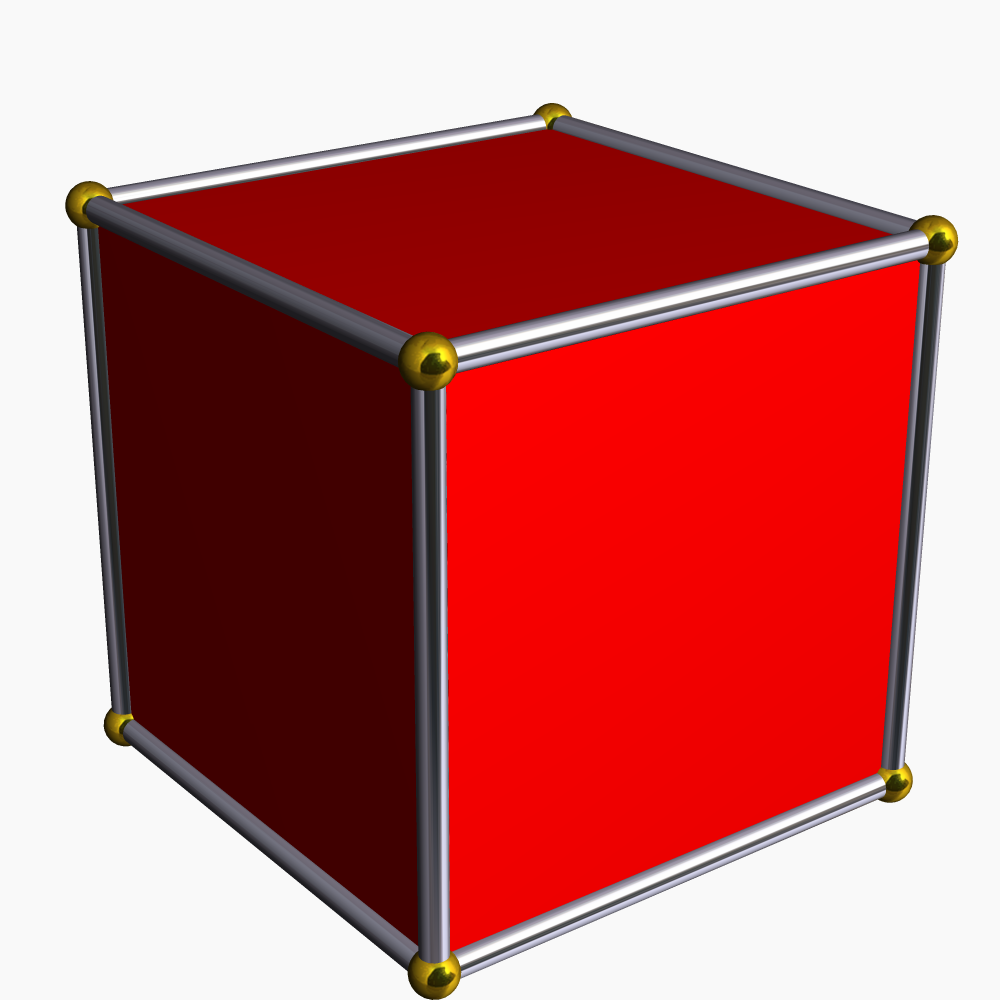
|
Hexahedron2
A hexahedron (plural: hexahedra or hexahedrons) or sexahedron (plural: sexahedra or sexahedrons) is any polyhedron with six faces. A cube, for example, is a regular hexahedron with all its faces square, and three squares around each vertex. There are seven topologically distinct ''convex'' hexahedra, one of which exists in two mirror image forms. There are three topologically distinct concave hexahedra. Two polyhedra are "topologically distinct" if they have intrinsically different arrangements of faces and vertices, such that it is impossible to distort one into the other simply by changing the lengths of edges or the angles between edges or faces. Convex, Cuboid Convex, Others Concave There are three further topologically distinct hexahedra that can only be realised as ''concave'' figures: A digonal antiprism can be considered a degenerate form of hexahedron, having two opposing digonal faces and four triangular faces. However, digons are usually disregarded in the defi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Hexahedron2
A hexahedron (plural: hexahedra or hexahedrons) or sexahedron (plural: sexahedra or sexahedrons) is any polyhedron with six faces. A cube, for example, is a regular hexahedron with all its faces square, and three squares around each vertex. There are seven topologically distinct ''convex'' hexahedra, one of which exists in two mirror image forms. There are three topologically distinct concave hexahedra. Two polyhedra are "topologically distinct" if they have intrinsically different arrangements of faces and vertices, such that it is impossible to distort one into the other simply by changing the lengths of edges or the angles between edges or faces. Convex, Cuboid Convex, Others Concave There are three further topologically distinct hexahedra that can only be realised as ''concave'' figures: A digonal antiprism can be considered a degenerate form of hexahedron, having two opposing digonal faces and four triangular faces. However, digons are usually disregarded in the defi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Hexahedron
A hexahedron (plural: hexahedra or hexahedrons) or sexahedron (plural: sexahedra or sexahedrons) is any polyhedron with six faces. A cube, for example, is a regular hexahedron with all its faces square, and three squares around each vertex. There are seven topologically distinct ''convex'' hexahedra, one of which exists in two mirror image forms. There are three topologically distinct concave hexahedra. Two polyhedra are "topologically distinct" if they have intrinsically different arrangements of faces and vertices, such that it is impossible to distort one into the other simply by changing the lengths of edges or the angles between edges or faces. Convex, Cuboid Convex, Others Concave There are three further topologically distinct hexahedra that can only be realised as ''concave'' figures: A digonal antiprism can be considered a degenerate form of hexahedron, having two opposing digonal faces and four triangular faces. However, digons are usually disregarded in the defi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Polyhedron
In geometry, a polyhedron (plural polyhedra or polyhedrons; ) is a three-dimensional shape with flat polygonal faces, straight edges and sharp corners or vertices. A convex polyhedron is the convex hull of finitely many points, not all on the same plane. Cubes and pyramids are examples of convex polyhedra. A polyhedron is a 3-dimensional example of a polytope, a more general concept in any number of dimensions. Definition Convex polyhedra are well-defined, with several equivalent standard definitions. However, the formal mathematical definition of polyhedra that are not required to be convex has been problematic. Many definitions of "polyhedron" have been given within particular contexts,. some more rigorous than others, and there is not universal agreement over which of these to choose. Some of these definitions exclude shapes that have often been counted as polyhedra (such as the self-crossing polyhedra) or include shapes that are often not considered as valid polyhedr ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Rhombus
In plane Euclidean geometry, a rhombus (plural rhombi or rhombuses) is a quadrilateral whose four sides all have the same length. Another name is equilateral quadrilateral, since equilateral means that all of its sides are equal in length. The rhombus is often called a "diamond", after the diamonds suit in playing cards which resembles the projection of an octahedral diamond, or a lozenge, though the former sometimes refers specifically to a rhombus with a 60° angle (which some authors call a calisson after the French sweet – also see Polyiamond), and the latter sometimes refers specifically to a rhombus with a 45° angle. Every rhombus is simple (non-self-intersecting), and is a special case of a parallelogram and a kite. A rhombus with right angles is a square. Etymology The word "rhombus" comes from grc, ῥόμβος, rhombos, meaning something that spins, which derives from the verb , romanized: , meaning "to turn round and round." The word was used both by Eucl ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Triangular Bipyramid
In geometry, the triangular bipyramid (or dipyramid) is a type of hexahedron, being the first in the infinite set of face-transitive bipyramids. It is the dual of the triangular prism with 6 isosceles triangle faces. As the name suggests, it can be constructed by joining two tetrahedra along one face. Although all its faces are congruent and the solid is face-transitive, it is not a Platonic solid because some vertices adjoin three faces and others adjoin four. The bipyramid whose six faces are all equilateral triangles is one of the Johnson solids, (). As a Johnson solid with all faces equilateral triangles, it is also a deltahedron. Formulae The following formulae for the height (H), surface area (A) and volume (V) can be used if all faces are regular, with edge length L: :H = L\cdot \frac \approx L\cdot 1.632993162 :A = L^2 \cdot \frac \approx L^2\cdot 2.598076211 :V = L^3 \cdot \frac \approx L^3\cdot 0.235702260 Dual polyhedron The dual polyhedron of the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Parallelogram
In Euclidean geometry, a parallelogram is a simple (non- self-intersecting) quadrilateral with two pairs of parallel sides. The opposite or facing sides of a parallelogram are of equal length and the opposite angles of a parallelogram are of equal measure. The congruence of opposite sides and opposite angles is a direct consequence of the Euclidean parallel postulate and neither condition can be proven without appealing to the Euclidean parallel postulate or one of its equivalent formulations. By comparison, a quadrilateral with just one pair of parallel sides is a trapezoid in American English or a trapezium in British English. The three-dimensional counterpart of a parallelogram is a parallelepiped. The etymology (in Greek παραλληλ-όγραμμον, ''parallēl-ógrammon'', a shape "of parallel lines") reflects the definition. Special cases *Rectangle – A parallelogram with four angles of equal size (right angles). *Rhombus – A parallelogram with four sides of eq ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
