|
Hexagonal Pyramid
In geometry, a hexagonal pyramid is a pyramid with a hexagonal base upon which are erected six isosceles triangular faces that meet at a point (the apex). Like any pyramid, it is self- dual. A right hexagonal pyramid with a regular hexagon base has ''C''6v symmetry. A right regular pyramid is one which has a regular polygon as its base and whose apex is "above" the center of the base, so that the apex, the center of the base and any other vertex form a right triangle. Vertex coordinates A hexagonal pyramid of edge length 1 has the following vertices: *\left(\pm\frac12,\,\pm\frac,\,0\right) *\left(\pm1,\,0,\,0\right) *\left(0,\,0,\,0\right) These coordinates are a subset of the vertices of the regular triangular tiling. Representations A hexagonal pyramid has the following Coxeter diagrams: *ox6oo&#x (full symmetry) *ox3ox&#x (generally a ditrigonal pyramid) Related polyhedra See also * Bipyramid, prism and antiprism In geometry, an antiprism or is a poly ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Pyramid (geometry)
In geometry, a pyramid () is a polyhedron formed by connecting a polygonal base and a point, called the apex. Each base edge and apex form a triangle, called a ''lateral face''. It is a conic solid with polygonal base. A pyramid with an base has vertices, faces, and edges. All pyramids are self-dual. A right pyramid has its apex directly above the centroid of its base. Nonright pyramids are called oblique pyramids. A regular pyramid has a regular polygon base and is usually implied to be a ''right pyramid''. When unspecified, a pyramid is usually assumed to be a ''regular'' square pyramid, like the physical pyramid structures. A triangle-based pyramid is more often called a tetrahedron. Among oblique pyramids, like acute and obtuse triangles, a pyramid can be called ''acute'' if its apex is above the interior of the base and ''obtuse'' if its apex is above the exterior of the base. A right-angled pyramid has its apex above an edge or vertex of the base. In a tetrahedro ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Regular Polygon
In Euclidean geometry, a regular polygon is a polygon that is Equiangular polygon, direct equiangular (all angles are equal in measure) and Equilateral polygon, equilateral (all sides have the same length). Regular polygons may be either convex polygon, convex, star polygon, star or Skew polygon, skew. In the limit (mathematics), limit, a sequence of regular polygons with an increasing number of sides approximates a circle, if the perimeter or area is fixed, or a regular apeirogon (effectively a Line (geometry), straight line), if the edge length is fixed. General properties ''These properties apply to all regular polygons, whether convex or star polygon, star.'' A regular ''n''-sided polygon has rotational symmetry of order ''n''. All vertices of a regular polygon lie on a common circle (the circumscribed circle); i.e., they are concyclic points. That is, a regular polygon is a cyclic polygon. Together with the property of equal-length sides, this implies that every regular p ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Pyramids And Bipyramids
A pyramid (from el, πυραμίς ') is a structure whose outer surfaces are triangular and converge to a single step at the top, making the shape roughly a pyramid in the geometric sense. The base of a pyramid can be trilateral, quadrilateral, or of any polygon shape. As such, a pyramid has at least three outer triangular surfaces (at least four faces including the base). The square pyramid, with a square base and four triangular outer surfaces, is a common version. A pyramid's design, with the majority of the weight closer to the ground and with the pyramidion at the apex, means that less material higher up on the pyramid will be pushing down from above. This distribution of weight allowed early civilizations to create stable monumental structures. Civilizations in many parts of the world have built pyramids. The largest pyramid by volume is the Great Pyramid of Cholula, in the Mexican state of Puebla. For thousands of years, the largest structures on Earth were pyramids ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Antiprism
In geometry, an antiprism or is a polyhedron composed of two parallel direct copies (not mirror images) of an polygon, connected by an alternating band of triangles. They are represented by the Conway notation . Antiprisms are a subclass of prismatoids, and are a (degenerate) type of snub polyhedron. Antiprisms are similar to prisms, except that the bases are twisted relatively to each other, and that the side faces (connecting the bases) are triangles, rather than quadrilaterals. The dual polyhedron of an -gonal antiprism is an -gonal trapezohedron. History At the intersection of modern-day graph theory and coding theory, the triangulation of a set of points have interested mathematicians since Isaac Newton, who fruitlessly sought a mathematical proof of the kissing number problem in 1694. The existence of antiprisms was discussed, and their name was coined by Johannes Kepler, though it is possible that they were previously known to Archimedes, as they satisfy the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Prism (geometry)
In geometry, a prism is a polyhedron comprising an polygon Base (geometry), base, a second base which is a Translation (geometry), translated copy (rigidly moved without rotation) of the first, and other Face (geometry), faces, necessarily all parallelograms, joining corresponding sides of the two bases. All Cross section (geometry), cross-sections parallel to the bases are translations of the bases. Prisms are named after their bases, e.g. a prism with a pentagonal base is called a pentagonal prism. Prisms are a subclass of prismatoids. Like many basic geometric terms, the word ''prism'' () was first used in Euclid's Elements. Euclid defined the term in Book XI as “a solid figure contained by two opposite, equal and parallel planes, while the rest are parallelograms”. However, this definition has been criticized for not being specific enough in relation to the nature of the bases, which caused confusion among later geometry writers. Oblique prism An oblique prism is a pr ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Bipyramid
A (symmetric) -gonal bipyramid or dipyramid is a polyhedron formed by joining an -gonal pyramid and its mirror image base-to-base. An -gonal bipyramid has triangle faces, edges, and vertices. The "-gonal" in the name of a bipyramid does not refer to a face but to the internal polygon base, lying in the mirror plane that connects the two pyramid halves. (If it were a face, then each of its edges would connect three faces instead of two.) "Regular", right bipyramids A ''"regular"'' bipyramid has a ''regular'' polygon base. It is usually implied to be also a ''right'' bipyramid. A ''right'' bipyramid has its two apices ''right'' above and ''right'' below the center or the ''centroid'' of its polygon base. A "regular" right (symmetric) -gonal bipyramid has Schläfli symbol . A right (symmetric) bipyramid has Schläfli symbol , for polygon base . The "regular" right (thus face-transitive) -gonal bipyramid with regular vertices is the dual of the -gonal uniform (thus right) ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Coxeter Diagram
Harold Scott MacDonald "Donald" Coxeter, (9 February 1907 – 31 March 2003) was a British and later also Canadian geometer. He is regarded as one of the greatest geometers of the 20th century. Biography Coxeter was born in Kensington to Harold Samuel Coxeter and Lucy (). His father had taken over the family business of Coxeter & Son, manufacturers of surgical instruments and compressed gases (including a mechanism for anaesthetising surgical patients with nitrous oxide), but was able to retire early and focus on sculpting and baritone singing; Lucy Coxeter was a portrait and landscape painter who had attended the Royal Academy of Arts. A maternal cousin was the architect Sir Giles Gilbert Scott. In his youth, Coxeter composed music and was an accomplished pianist at the age of 10. Roberts, Siobhan, ''King of Infinite Space: Donald Coxeter, The Man Who Saved Geometry'', Walker & Company, 2006, He felt that mathematics and music were intimately related, outlining his ide ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
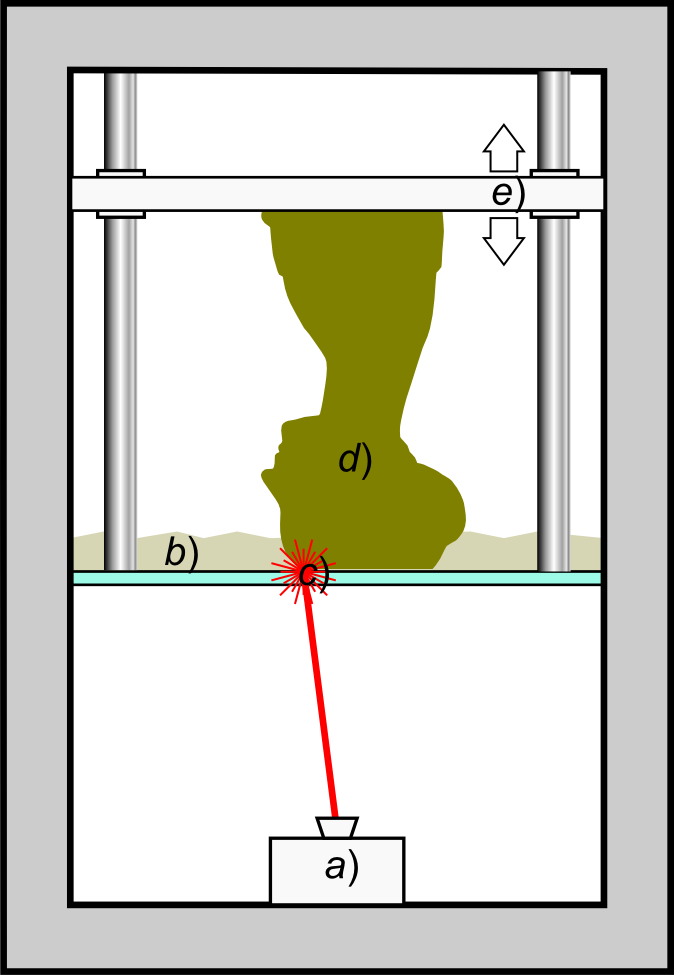
Stereolithography
Stereolithography (SLA or SL; also known as vat photopolymerisation, optical fabrication, photo-solidification, or resin printing) is a form of 3D printing technology used for creating models, prototypes, patterns, and production parts in a layer by layer fashion using photochemical processes by which light causes chemical monomers and oligomers to cross-link together to form polymers.U.S. Patentbr>4,575,330(“Apparatus for Production of Three-Dimensional Objects by Stereolithography”) Those polymers then make up the body of a three-dimensional solid. Research in the area had been conducted during the 1970s, but the term was coined by Chuck Hull in 1984 when he applied for a patent on the process, which was granted in 1986. Stereolithography can be used to create prototypes for products in development, medical models, and computer hardware, as well as in many other applications. While stereolithography is fast and can produce almost any design, it can be expensive. History ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Right Triangle
A right triangle (American English) or right-angled triangle (British), or more formally an orthogonal triangle, formerly called a rectangled triangle ( grc, ὀρθόσγωνία, lit=upright angle), is a triangle in which one angle is a right angle (that is, a 90-degree angle), i.e., in which two sides are perpendicular. The relation between the sides and other angles of the right triangle is the basis for trigonometry. The side opposite to the right angle is called the ''hypotenuse'' (side ''c'' in the figure). The sides adjacent to the right angle are called ''legs'' (or ''catheti'', singular: ''cathetus''). Side ''a'' may be identified as the side ''adjacent to angle B'' and ''opposed to'' (or ''opposite'') ''angle A'', while side ''b'' is the side ''adjacent to angle A'' and ''opposed to angle B''. If the lengths of all three sides of a right triangle are integers, the triangle is said to be a Pythagorean triangle and its side lengths are collectively known as a ''Pythagor ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
List Of Spherical Symmetry Groups
Finite spherical symmetry groups are also called point groups in three dimensions. There are five fundamental symmetry classes which have triangular fundamental domains: dihedral, cyclic, tetrahedral, octahedral, and icosahedral symmetry. This article lists the groups by Schoenflies notation, Coxeter notation, orbifold notation, and order. John Conway uses a variation of the Schoenflies notation, based on the groups' quaternion algebraic structure, labeled by one or two upper case letters, and whole number subscripts. The group order is defined as the subscript, unless the order is doubled for symbols with a plus or minus, "±", prefix, which implies a central inversion. Hermann–Mauguin notation (International notation) is also given. The crystallography groups, 32 in total, are a subset with element orders 2, 3, 4 and 6.Sands, 1993 Involutional symmetry There are four involutional groups: no symmetry (C1), reflection symmetry (Cs), 2-fold rotational symmetry (C2), and cent ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Triangle
A triangle is a polygon with three Edge (geometry), edges and three Vertex (geometry), vertices. It is one of the basic shapes in geometry. A triangle with vertices ''A'', ''B'', and ''C'' is denoted \triangle ABC. In Euclidean geometry, any three points, when non-Collinearity, collinear, determine a unique triangle and simultaneously, a unique Plane (mathematics), plane (i.e. a two-dimensional Euclidean space). In other words, there is only one plane that contains that triangle, and every triangle is contained in some plane. If the entire geometry is only the Euclidean plane, there is only one plane and all triangles are contained in it; however, in higher-dimensional Euclidean spaces, this is no longer true. This article is about triangles in Euclidean geometry, and in particular, the Euclidean plane, except where otherwise noted. Types of triangle The terminology for categorizing triangles is more than two thousand years old, having been defined on the very first page of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Dual Polyhedron
In geometry, every polyhedron is associated with a second dual structure, where the vertices of one correspond to the faces of the other, and the edges between pairs of vertices of one correspond to the edges between pairs of faces of the other. Such dual figures remain combinatorial or abstract polyhedra, but not all can also be constructed as geometric polyhedra. Starting with any given polyhedron, the dual of its dual is the original polyhedron. Duality preserves the symmetries of a polyhedron. Therefore, for many classes of polyhedra defined by their symmetries, the duals belong to a corresponding symmetry class. For example, the regular polyhedrathe (convex) Platonic solids and (star) Kepler–Poinsot polyhedraform dual pairs, where the regular tetrahedron is self-dual. The dual of an isogonal polyhedron (one in which any two vertices are equivalent under symmetries of the polyhedron) is an isohedral polyhedron (one in which any two faces are equivalent .., and vice vers ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
