|
Hermite's Problem
Hermite's problem is an open problem in mathematics posed by Charles Hermite in 1848. He asked for a way of expressing real numbers as sequences of natural numbers, such that the sequence is eventually periodic precisely when the original number is a cubic irrational. Motivation A standard way of writing real numbers is by their decimal representation, such as: :x=a_0.a_1a_2a_3\ldots\ where ''a''0 is an integer, the integer part of ''x'', and ''a''1, ''a''2, ''a''3, … are integers between 0 and 9. Given this representation the number ''x'' is equal to :x=\sum_^\infty \frac. The real number ''x'' is a rational number only if its decimal expansion is eventually periodic, that is if there are natural numbers ''N'' and ''p'' such that for every ''n'' ≥ ''N'' it is the case that ''a''''n''+''p'' = ''a''''n''. Another way of expressing numbers is to write them as continued fractions, as in: :x= _0;a_1,a_2,a_3,\ldots\ where ''a''0 is an integer an ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mathematics
Mathematics is an area of knowledge that includes the topics of numbers, formulas and related structures, shapes and the spaces in which they are contained, and quantities and their changes. These topics are represented in modern mathematics with the major subdisciplines of number theory, algebra, geometry, and analysis, respectively. There is no general consensus among mathematicians about a common definition for their academic discipline. Most mathematical activity involves the discovery of properties of abstract objects and the use of pure reason to prove them. These objects consist of either abstractions from nature orin modern mathematicsentities that are stipulated to have certain properties, called axioms. A ''proof'' consists of a succession of applications of deductive rules to already established results. These results include previously proved theorems, axioms, andin case of abstraction from naturesome basic properties that are considered true starting points of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Polynomial
In mathematics, a polynomial is an expression consisting of indeterminates (also called variables) and coefficients, that involves only the operations of addition, subtraction, multiplication, and positive-integer powers of variables. An example of a polynomial of a single indeterminate is . An example with three indeterminates is . Polynomials appear in many areas of mathematics and science. For example, they are used to form polynomial equations, which encode a wide range of problems, from elementary word problems to complicated scientific problems; they are used to define polynomial functions, which appear in settings ranging from basic chemistry and physics to economics and social science; they are used in calculus and numerical analysis to approximate other functions. In advanced mathematics, polynomials are used to construct polynomial rings and algebraic varieties, which are central concepts in algebra and algebraic geometry. Etymology The word ''polynomial'' join ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Continued Fractions
In mathematics, a continued fraction is an expression obtained through an iterative process of representing a number as the sum of its integer part and the reciprocal of another number, then writing this other number as the sum of its integer part and another reciprocal, and so on. In a finite continued fraction (or terminated continued fraction), the iteration/recursion is terminated after finitely many steps by using an integer in lieu of another continued fraction. In contrast, an infinite continued fraction is an infinite expression. In either case, all integers in the sequence, other than the first, must be positive. The integers a_i are called the coefficients or terms of the continued fraction. It is generally assumed that the numerator of all of the fractions is 1. If arbitrary values and/or functions are used in place of one or more of the numerators or the integers in the denominators, the resulting expression is a generalized continued fraction. When it is necessary t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Simplex
In geometry, a simplex (plural: simplexes or simplices) is a generalization of the notion of a triangle or tetrahedron to arbitrary dimensions. The simplex is so-named because it represents the simplest possible polytope in any given dimension. For example, * a 0-dimensional simplex is a point, * a 1-dimensional simplex is a line segment, * a 2-dimensional simplex is a triangle, * a 3-dimensional simplex is a tetrahedron, and * a 4-dimensional simplex is a 5-cell. Specifically, a ''k''-simplex is a ''k''-dimensional polytope which is the convex hull of its ''k'' + 1 vertices. More formally, suppose the ''k'' + 1 points u_0, \dots, u_k \in \mathbb^ are affinely independent, which means u_1 - u_0,\dots, u_k-u_0 are linearly independent. Then, the simplex determined by them is the set of points : C = \left\ This representation in terms of weighted vertices is known as the barycentric coordinate system. A regular simplex is a simplex that is also a regular polytope. A ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Unit Square
In mathematics, a unit square is a square whose sides have length . Often, ''the'' unit square refers specifically to the square in the Cartesian plane with corners at the four points ), , , and . Cartesian coordinates In a Cartesian coordinate system with coordinates , a unit square is defined as a square consisting of the points where both and lie in a closed unit interval from to . That is, a unit square is the Cartesian product , where denotes the closed unit interval. Complex coordinates The unit square can also be thought of as a subset of the complex plane, the topological space formed by the complex numbers. In this view, the four corners of the unit square are at the four complex numbers , , , and . Rational distance problem It is not known whether any point in the plane is a rational distance from all four vertices of the unit square.. See also * Unit circle * Unit cube * Unit sphere In mathematics, a unit sphere is simply a sphere of radius one around a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Dyadic Rational
In mathematics, a dyadic rational or binary rational is a number that can be expressed as a fraction whose denominator is a power of two. For example, 1/2, 3/2, and 3/8 are dyadic rationals, but 1/3 is not. These numbers are important in computer science because they are the only ones with finite binary representations. Dyadic rationals also have applications in weights and measures, musical time signatures, and early mathematics education. They can accurately approximate any real number. The sum, difference, or product of any two dyadic rational numbers is another dyadic rational number, given by a simple formula. However, division of one dyadic rational number by another does not always produce a dyadic rational result. Mathematically, this means that the dyadic rational numbers form a ring, lying between the ring of integers and the field of rational numbers. This ring may be denoted \Z tfrac12/math>. In advanced mathematics, the dyadic rational numbers are central to the con ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
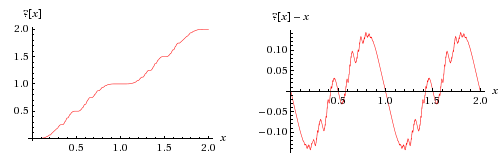
Minkowski's Question Mark Function
In mathematics, the Minkowski question-mark function, denoted , is a function with unusual fractal properties, defined by Hermann Minkowski in 1904. It maps quadratic irrational numbers to rational numbers on the unit interval, via an expression relating the continued fraction expansions of the quadratics to the binary expansions of the rationals, given by Arnaud Denjoy in 1938. It also maps rational numbers to dyadic rationals, as can be seen by a recursive definition closely related to the Stern–Brocot tree. Definition and intuition One way to define the question-mark function involves the correspondence between two different ways of representing fractional numbers using finite or infinite binary sequences. Most familiarly, a string of 0's and 1's with a single point mark ".", like "11.001001000011111..." can be interpreted as the binary representation of a number. In this case this number is 2+1+\frac18+\frac1+\cdots=\pi. There is a different way of interpreting the same s ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Minimal Polynomial (field Theory)
In field theory, a branch of mathematics, the minimal polynomial of an element of a field is, roughly speaking, the polynomial of lowest degree having coefficients in the field, such that is a root of the polynomial. If the minimal polynomial of exists, it is unique. The coefficient of the highest-degree term in the polynomial is required to be 1, and the type for the remaining coefficients could be integers, rational numbers, real numbers, or others. More formally, a minimal polynomial is defined relative to a field extension and an element of the extension field . The minimal polynomial of an element, if it exists, is a member of , the ring of polynomials in the variable with coefficients in . Given an element of , let be the set of all polynomials in such that . The element is called a root or zero of each polynomial in . The set is so named because it is an ideal of . The zero polynomial, all of whose coefficients are 0, is in every since for all and . This ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Cubic Field
In mathematics, specifically the area of algebraic number theory, a cubic field is an algebraic number field of degree three. Definition If ''K'' is a field extension of the rational numbers Q of degree 'K'':Qnbsp;= 3, then ''K'' is called a cubic field. Any such field is isomorphic to a field of the form :\mathbf (f(x)) where ''f'' is an irreducible cubic polynomial with coefficients in Q. If ''f'' has three real roots, then ''K'' is called a totally real cubic field and it is an example of a totally real field. If, on the other hand, ''f'' has a non-real root, then ''K'' is called a complex cubic field. A cubic field ''K'' is called a cyclic cubic field if it contains all three roots of its generating polynomial ''f''. Equivalently, ''K'' is a cyclic cubic field if it is a Galois extension of Q, in which case its Galois group over Q is cyclic of order three. This can only happen if ''K'' is totally real. It is a rare occurrence in the sense that if the set of cubic field ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Generalized Continued Fraction
In complex analysis, a branch of mathematics, a generalized continued fraction is a generalization of regular continued fractions in canonical form, in which the partial numerators and partial denominators can assume arbitrary complex values. A generalized continued fraction is an expression of the form :x = b_0 + \cfrac where the () are the partial numerators, the are the partial denominators, and the leading term is called the ''integer'' part of the continued fraction. The successive convergents of the continued fraction are formed by applying the fundamental recurrence formulas: :\begin x_0 &= \frac = b_0, \\ pxx_1 &= \frac = \frac, \\ pxx_2 &= \frac = \frac,\ \dots \end where is the ''numerator'' and is the ''denominator'', called continuants, of the th convergent. They are given by the recursion :\begin A_n &= b_n A_ + a_n A_, \\ B_n &= b_n B_ + a_n B_ \qquad \text n \ge 1 \end with initial values :\begin A_ &= 1,& A_0&=b_0,\\ B_&=0, & B_0&=1. \end If the sequence ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Carl Gustav Jacob Jacobi
Carl Gustav Jacob Jacobi (; ; 10 December 1804 – 18 February 1851) was a German mathematician who made fundamental contributions to elliptic functions, dynamics, differential equations, determinants, and number theory. His name is occasionally written as Carolus Gustavus Iacobus Iacobi in his Latin books, and his first name is sometimes given as Karl. Jacobi was the first Jewish mathematician to be appointed professor at a German university. Biography Jacobi was born of Ashkenazi Jewish parentage in Potsdam on 10 December 1804. He was the second of four children of banker Simon Jacobi. His elder brother Moritz von Jacobi would also become known later as an engineer and physicist. He was initially home schooled by his uncle Lehman, who instructed him in the classical languages and elements of mathematics. In 1816, the twelve-year-old Jacobi went to the Potsdam Gymnasium, where students were taught all the standard subjects: classical languages, history, philology, mathem ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Set (mathematics)
A set is the mathematical model for a collection of different things; a set contains '' elements'' or ''members'', which can be mathematical objects of any kind: numbers, symbols, points in space, lines, other geometrical shapes, variables, or even other sets. The set with no element is the empty set; a set with a single element is a singleton. A set may have a finite number of elements or be an infinite set. Two sets are equal if they have precisely the same elements. Sets are ubiquitous in modern mathematics. Indeed, set theory, more specifically Zermelo–Fraenkel set theory, has been the standard way to provide rigorous foundations for all branches of mathematics since the first half of the 20th century. History The concept of a set emerged in mathematics at the end of the 19th century. The German word for set, ''Menge'', was coined by Bernard Bolzano in his work ''Paradoxes of the Infinite''. Georg Cantor, one of the founders of set theory, gave the following defin ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |