|
Hartle–Thorne Metric
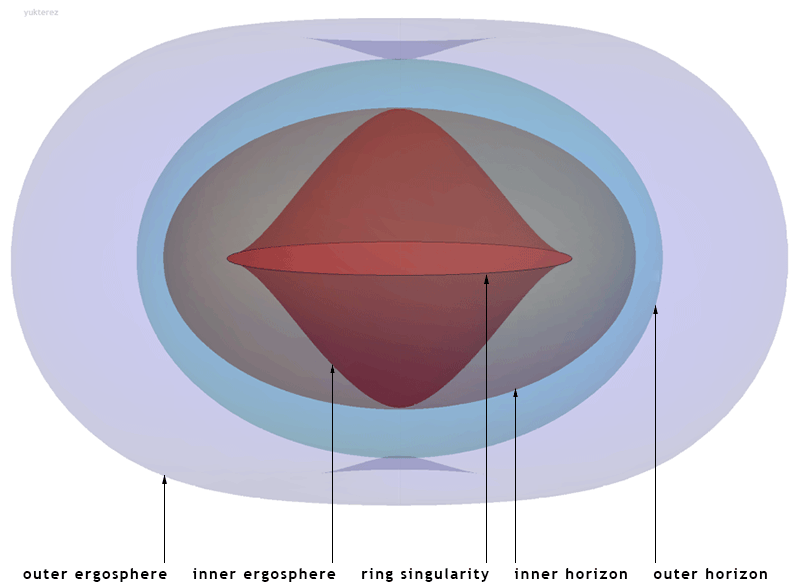
The Hartle–Thorne metric is an approximate solution of the vacuum Einstein field equations of general relativity that describes the exterior of a slowly and rigidly rotating, stationary and axially symmetric body. The metric was found by James Hartle and Kip Thorne in the 1960s to study the spacetime outside neutron stars, white dwarfs and supermassive stars. It can be shown that it is an approximation to the Kerr metric (which describes a rotating black hole) when the quadrupole moment is set as q=-a^2aM^3, which is the correct value for a black hole but not, in general, for other astrophysical objects. Metric Up to second order in the angular momentum J, mass M and quadrupole moment A quadrupole or quadrapole is one of a sequence of configurations of things like electric charge or current, or gravitational mass that can exist in ideal form, but it is usually just part of a multipole expansion of a more complex structure refl ... q, the metric in spherical coordinates ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Einstein Field Equations
In the general theory of relativity, the Einstein field equations (EFE; also known as Einstein's equations) relate the geometry of spacetime to the distribution of matter within it. The equations were published by Einstein in 1915 in the form of a tensor equation which related the local ' (expressed by the Einstein tensor) with the local energy, momentum and stress within that spacetime (expressed by the stress–energy tensor). Analogously to the way that electromagnetic fields are related to the distribution of charges and currents via Maxwell's equations, the EFE relate the spacetime geometry to the distribution of mass–energy, momentum and stress, that is, they determine the metric tensor of spacetime for a given arrangement of stress–energy–momentum in the spacetime. The relationship between the metric tensor and the Einstein tensor allows the EFE to be written as a set of nonlinear partial differential equations when used in this way. The solutions of the EF ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Axially Symmetric
In geometry, circular symmetry is a type of continuous symmetry for a planar object that can be rotated by any arbitrary angle and map onto itself. Rotational circular symmetry is isomorphic with the circle group in the complex plane, or the special orthogonal group SO(2), and unitary group U(1). Reflective circular symmetry is isomorphic with the orthogonal group O(2). Two dimensions A 2-dimensional object with circular symmetry would consist of concentric circles and annular domains. Rotational circular symmetry has all cyclic symmetry, Z''n'' as subgroup symmetries. Reflective circular symmetry has all dihedral symmetry, Dih''n'' as subgroup symmetries. Three dimensions In 3-dimensions, a surface or solid of revolution has circular symmetry around an axis, also called cylindrical symmetry or axial symmetry. An example is a right circular cone. Circular symmetry in 3 dimensions has all pyramidal symmetry, C''n''v as subgroups. A double-cone, bicone, cylin ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
James Hartle
James Burkett Hartle (August 20, 1939) is an American physicist. He has been a professor of physics at the University of California, Santa Barbara since 1966, and he is currently a member of the external faculty of the Santa Fe Institute. Hartle is known for his work in general relativity, astrophysics, and interpretation of quantum mechanics. Work In collaboration with Murray Gell-Mann and others, Hartle developed an alternative to the standard Copenhagen interpretation, more general and appropriate to quantum cosmology, based on consistent histories. With Dieter Brill in 1964, he discovered the Brill–Hartle geon, an approximate solution realizing Wheeler's suggestion of a hypothetical phenomenon in which a gravitational wave packet is confined to a compact region of spacetime by the gravitational attraction of its own field energy. With Kip Thorne, Hartle derived from general relativity the laws of motion and precession of black holes and other relativistic bodies, inclu ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Kip Thorne
Kip Stephen Thorne (born June 1, 1940) is an American theoretical physicist known for his contributions in gravitational physics and astrophysics. A longtime friend and colleague of Stephen Hawking and Carl Sagan, he was the Richard P. Feynman Professor of Theoretical Physics at the California Institute of Technology (Caltech) until 2009 and is one of the world's leading experts on the astrophysical implications of Einstein's general theory of relativity. He continues to do scientific research and scientific consulting, most notably for the Christopher Nolan film '' Interstellar''. Thorne was awarded the 2017 Nobel Prize in Physics along with Rainer Weiss and Barry C. Barish "for decisive contributions to the LIGO detector and the observation of gravitational waves". Life and career Thorne was born on June 1, 1940, in Logan, Utah. His father, D. Wynne Thorne (1908–1979), was a professor of soil chemistry at Utah State University, and his mother, Alison (née ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Neutron Stars
A neutron star is the collapsed core of a massive supergiant star, which had a total mass of between 10 and 25 solar masses, possibly more if the star was especially metal-rich. Except for black holes and some hypothetical objects (e.g. white holes, quark stars, and strange stars), neutron stars are the smallest and densest currently known class of stellar objects. Neutron stars have a radius on the order of and a mass of about 1.4 solar masses. They result from the supernova explosion of a massive star, combined with gravitational collapse, that compresses the core past white dwarf star density to that of atomic nuclei. Once formed, they no longer actively generate heat, and cool over time; however, they may still evolve further through collision or accretion. Most of the basic models for these objects imply that neutron stars are composed almost entirely of neutrons (subatomic particles with no net electrical charge and with slightly larger mass than protons); the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
White Dwarfs
A white dwarf is a stellar core remnant composed mostly of electron-degenerate matter. A white dwarf is very dense: its mass is comparable to the Sun's, while its volume is comparable to the Earth's. A white dwarf's faint luminosity comes from the emission of residual thermal energy; no fusion takes place in a white dwarf. The nearest known white dwarf is at 8.6 light years, the smaller component of the Sirius binary star. There are currently thought to be eight white dwarfs among the hundred star systems nearest the Sun. The unusual faintness of white dwarfs was first recognized in 1910. The name ''white dwarf'' was coined by Willem Luyten in 1922. White dwarfs are thought to be the final evolutionary state of stars whose mass is not high enough to become a neutron star or black hole. This includes over 97% of the other stars in the Milky Way. After the hydrogen- fusing period of a main-sequence star of low or medium mass ends, such a star will expand to a red ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Supermassive Stars
During 1944, Walter Baade categorized groups of stars within the Milky Way into stellar populations. In the abstract of the article by Baade, he recognizes that Jan Oort originally conceived this type of classification in 1926: Baade noticed that bluer stars were strongly associated with the spiral arms, and yellow stars dominated near the central galactic bulge and within globular star clusters. Two main divisions were defined as * Population I and * Population II, with another newer, hypothetical division called * Population III added in 1978; they are often simply abbreviated as Pop. I, Pop. II, and Pop. III. Among the population types, significant differences were found with their individual observed stellar spectra. These were later shown to be very important and were possibly related to star formation, observed kinematics, stellar age, and even galaxy evolution in both spiral and elliptical galaxies. These three simple population classes usef ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Kerr Metric
The Kerr metric or Kerr geometry describes the geometry of empty spacetime around a rotating uncharged axially symmetric black hole with a quasispherical event horizon. The Kerr metric is an exact solution of the Einstein field equations of general relativity; these equations are highly non-linear, which makes exact solutions very difficult to find. Overview The Kerr metric is a generalization to a rotating body of the Schwarzschild metric, discovered by Karl Schwarzschild in 1915, which described the geometry of spacetime around an uncharged, spherically symmetric, and non-rotating body. The corresponding solution for a ''charged'', spherical, non-rotating body, the Reissner–Nordström metric, was discovered soon afterwards (1916–1918). However, the exact solution for an uncharged, ''rotating'' black hole, the Kerr metric, remained unsolved until 1963, when it was discovered by Roy Kerr.Melia, Fulvio (2009). "Cracking the Einstein code: relativity and the birth of b ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Angular Momentum
In physics, angular momentum (rarely, moment of momentum or rotational momentum) is the rotational analog of linear momentum. It is an important physical quantity because it is a conserved quantity—the total angular momentum of a closed system remains constant. Angular momentum has both a direction and a magnitude, and both are conserved. Bicycles and motorcycles, frisbees, rifled bullets, and gyroscopes owe their useful properties to conservation of angular momentum. Conservation of angular momentum is also why hurricanes form spirals and neutron stars have high rotational rates. In general, conservation limits the possible motion of a system, but it does not uniquely determine it. The three-dimensional angular momentum for a point particle is classically represented as a pseudovector , the cross product of the particle's position vector (relative to some origin) and its momentum vector; the latter is in Newtonian mechanics. Unlike linear momentum, angular mome ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Quadrupole Moment
A quadrupole or quadrapole is one of a sequence of configurations of things like electric charge or current, or gravitational mass that can exist in ideal form, but it is usually just part of a multipole expansion of a more complex structure reflecting various orders of complexity. Mathematical definition The quadrupole moment tensor ''Q'' is a rank-two tensor—3×3 matrix. There are several definitions, but it is normally stated in the traceless form (i.e. Q_ + Q_ + Q_ = 0). The quadrupole moment tensor has thus nine components, but because of transposition symmetry and zero-trace property, in this form only five of these are independent. For a discrete system of \ell point charges or masses in the case of a gravitational quadrupole, each with charge q_\ell, or mass m_\ell, and position \vec_\ell = \left(r_, r_, r_\right) relative to the coordinate system origin, the components of the ''Q'' matrix are defined by: : Q_ = \sum_\ell q_\ell\left(3r_ r_ - \left\, \vec_\ell \rig ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Spherical Coordinates
In mathematics, a spherical coordinate system is a coordinate system for three-dimensional space where the position of a point is specified by three numbers: the ''radial distance'' of that point from a fixed origin, its ''polar angle'' measured from a fixed zenith direction, and the '' azimuthal angle'' of its orthogonal projection on a reference plane that passes through the origin and is orthogonal to the zenith, measured from a fixed reference direction on that plane. It can be seen as the three-dimensional version of the polar coordinate system. The radial distance is also called the ''radius'' or ''radial coordinate''. The polar angle may be called '' colatitude'', '' zenith angle'', '' normal angle'', or '' inclination angle''. When radius is fixed, the two angular coordinates make a coordinate system on the sphere sometimes called spherical polar coordinates. The use of symbols and the order of the coordinates differs among sources and disciplines. This article wi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
General Relativity
General relativity, also known as the general theory of relativity and Einstein's theory of gravity, is the geometric theory of gravitation published by Albert Einstein in 1915 and is the current description of gravitation in modern physics. General relativity generalizes special relativity and refines Newton's law of universal gravitation, providing a unified description of gravity as a geometric property of space and time or four-dimensional spacetime. In particular, the ' is directly related to the energy and momentum of whatever matter and radiation are present. The relation is specified by the Einstein field equations, a system of second order partial differential equations. Newton's law of universal gravitation, which describes classical gravity, can be seen as a prediction of general relativity for the almost flat spacetime geometry around stationary mass distributions. Some predictions of general relativity, however, are beyond Newton's law of universal gr ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |



.jpg)