|
Harmonic Mean
In mathematics, the harmonic mean is one of several kinds of average, and in particular, one of the Pythagorean means. It is sometimes appropriate for situations when the average rate is desired. The harmonic mean can be expressed as the reciprocal of the arithmetic mean of the reciprocals of the given set of observations. As a simple example, the harmonic mean of 1, 4, and 4 is : \left(\frac\right)^ = \frac = \frac = 2\,. Definition The harmonic mean ''H'' of the positive real numbers x_1, x_2, \ldots, x_n is defined to be :H = \frac = \frac = \left(\frac\right)^. The third formula in the above equation expresses the harmonic mean as the reciprocal of the arithmetic mean of the reciprocals. From the following formula: :H = \frac. it is more apparent that the harmonic mean is related to the arithmetic and geometric means. It is the reciprocal dual of the arithmetic mean for positive inputs: :1/H(1/x_1 \ldots 1/x_n) = A(x_1 \ldots x_n) The harmonic mean is a Schur-con ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mathematics
Mathematics is an area of knowledge that includes the topics of numbers, formulas and related structures, shapes and the spaces in which they are contained, and quantities and their changes. These topics are represented in modern mathematics with the major subdisciplines of number theory, algebra, geometry, and analysis, respectively. There is no general consensus among mathematicians about a common definition for their academic discipline. Most mathematical activity involves the discovery of properties of abstract objects and the use of pure reason to prove them. These objects consist of either abstractions from nature orin modern mathematicsentities that are stipulated to have certain properties, called axioms. A ''proof'' consists of a succession of applications of deductive rules to already established results. These results include previously proved theorems, axioms, andin case of abstraction from naturesome basic properties that are considered true starting points of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Inequality Of Arithmetic And Geometric Means
In mathematics, the inequality of arithmetic and geometric means, or more briefly the AM–GM inequality, states that the arithmetic mean of a list of non-negative real numbers is greater than or equal to the geometric mean of the same list; and further, that the two means are equal if and only if every number in the list is the same (in which case they are both that number). The simplest non-trivial case – i.e., with more than one variable – for two non-negative numbers and , is the statement that :\frac2 \ge \sqrt with equality if and only if . This case can be seen from the fact that the square of a real number is always non-negative (greater than or equal to zero) and from the elementary case of the binomial formula: :\begin 0 & \le (x-y)^2 \\ & = x^2-2xy+y^2 \\ & = x^2+2xy+y^2 - 4xy \\ & = (x+y)^2 - 4xy. \end Hence , with equality precisely when , i.e. . The AM–GM inequality then follows from taking the positive square root of both sides and then dividing both ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Focal Length
The focal length of an optical system is a measure of how strongly the system converges or diverges light; it is the inverse of the system's optical power. A positive focal length indicates that a system converges light, while a negative focal length indicates that the system diverges light. A system with a shorter focal length bends the rays more sharply, bringing them to a focus in a shorter distance or diverging them more quickly. For the special case of a thin lens in air, a positive focal length is the distance over which initially collimated (parallel) rays are brought to a focus, or alternatively a negative focal length indicates how far in front of the lens a point source must be located to form a collimated beam. For more general optical systems, the focal length has no intuitive meaning; it is simply the inverse of the system's optical power. In most photography and all telescopy, where the subject is essentially infinitely far away, longer focal length (lower opti ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Optic Equation
In number theory, the optic equation is an equation that requires the sum of the reciprocals of two positive integers ''a'' and ''b'' to equal the reciprocal of a third positive integer ''c'':Dickson, L. E., ''History of the Theory of Numbers, Volume II: Diophantine Analysis'', Chelsea Publ. Co., 1952, pp. 688–691. :\frac+\frac=\frac. Multiplying both sides by ''abc'' shows that the optic equation is equivalent to a Diophantine equation (a polynomial equation in multiple integer variables). Solution All solutions in integers ''a, b, c'' are given in terms of positive integer parameters ''m, n, k'' by :a=km(m+n) , \quad b=kn(m+n), \quad c=kmn where ''m'' and ''n'' are coprime. Appearances in geometry The optic equation, permitting but not requiring integer solutions, appears in several contexts in geometry. In a bicentric quadrilateral, the inradius ''r'', the circumradius ''R'', and the distance ''x'' between the incenter and the circumcenter are related by Fuss' the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Inductor
An inductor, also called a coil, choke, or reactor, is a passive two-terminal electrical component that stores energy in a magnetic field when electric current flows through it. An inductor typically consists of an insulated wire wound into a coil. When the current flowing through the coil changes, the time-varying magnetic field induces an electromotive force (''emf'') (voltage) in the conductor, described by Faraday's law of induction. According to Lenz's law, the induced voltage has a polarity (direction) which opposes the change in current that created it. As a result, inductors oppose any changes in current through them. An inductor is characterized by its inductance, which is the ratio of the voltage to the rate of change of current. In the International System of Units (SI), the unit of inductance is the henry (H) named for 19th century American scientist Joseph Henry. In the measurement of magnetic circuits, it is equivalent to . Inductors have values that typically ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Capacitor
A capacitor is a device that stores electrical energy in an electric field by virtue of accumulating electric charges on two close surfaces insulated from each other. It is a passive electronic component with two terminals. The effect of a capacitor is known as capacitance. While some capacitance exists between any two electrical conductors in proximity in a circuit, a capacitor is a component designed to add capacitance to a circuit. The capacitor was originally known as the condenser, a term still encountered in a few compound names, such as the ''condenser microphone''. The physical form and construction of practical capacitors vary widely and many types of capacitor are in common use. Most capacitors contain at least two electrical conductors often in the form of metallic plates or surfaces separated by a dielectric medium. A conductor may be a foil, thin film, sintered bead of metal, or an electrolyte. The nonconducting dielectric acts to increase the capacitor's c ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
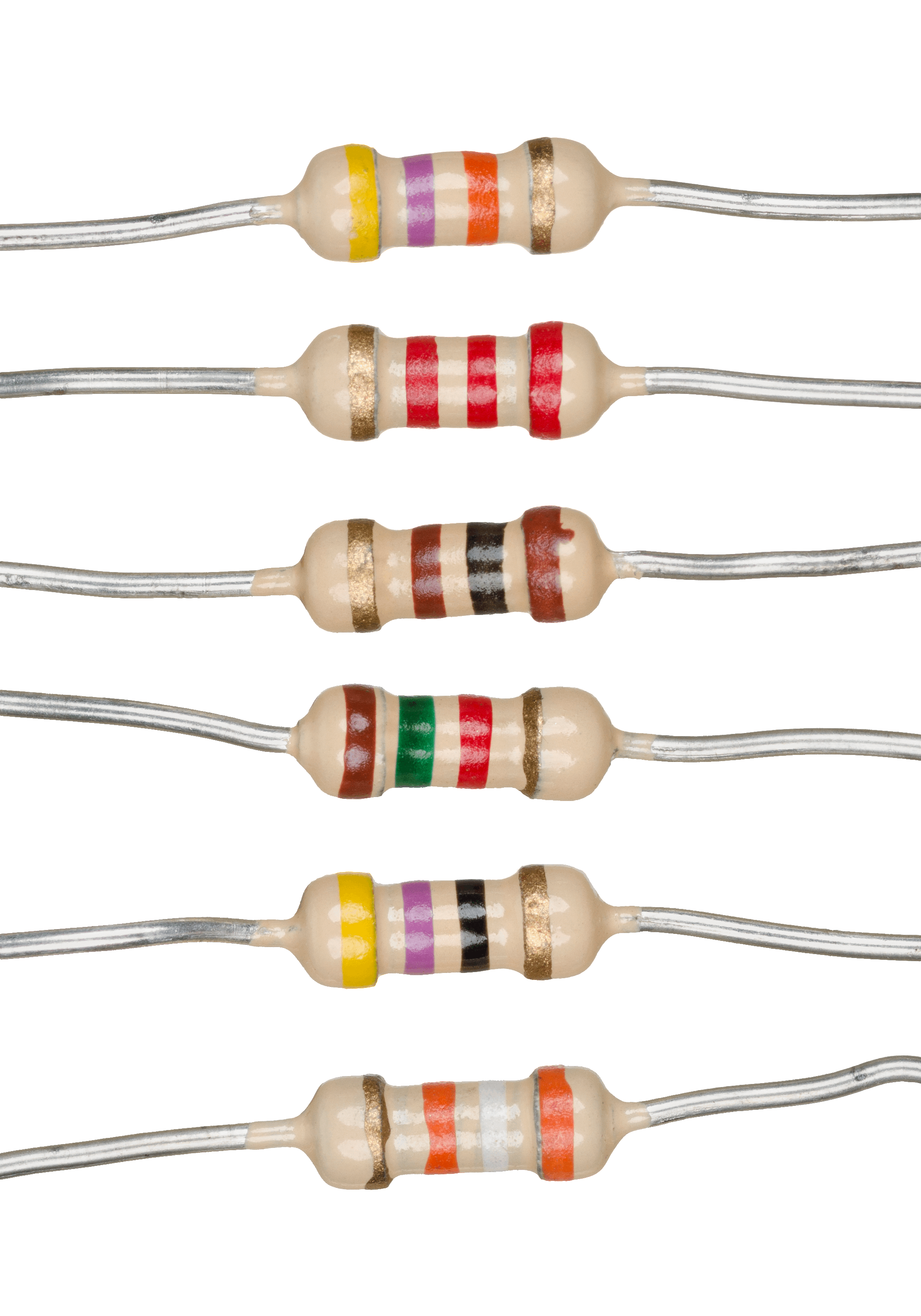
Resistor
A resistor is a passive two-terminal electrical component that implements electrical resistance as a circuit element. In electronic circuits, resistors are used to reduce current flow, adjust signal levels, to divide voltages, bias active elements, and terminate transmission lines, among other uses. High-power resistors that can dissipate many watts of electrical power as heat may be used as part of motor controls, in power distribution systems, or as test loads for generators. Fixed resistors have resistances that only change slightly with temperature, time or operating voltage. Variable resistors can be used to adjust circuit elements (such as a volume control or a lamp dimmer), or as sensing devices for heat, light, humidity, force, or chemical activity. Resistors are common elements of electrical networks and electronic circuits and are ubiquitous in electronic equipment. Practical resistors as discrete components can be composed of various compounds and forms. Resisto ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Dimensional Analysis
In engineering and science, dimensional analysis is the analysis of the relationships between different physical quantities by identifying their base quantities (such as length, mass, time, and electric current) and units of measure (such as miles vs. kilometres, or pounds vs. kilograms) and tracking these dimensions as calculations or comparisons are performed. The conversion of units from one dimensional unit to another is often easier within the metric or the SI than in others, due to the regular 10-base in all units. ''Commensurable'' physical quantities are of the same kind and have the same dimension, and can be directly compared to each other, even if they are expressed in differing units of measure, e.g. yards and metres, pounds (mass) and kilograms, seconds and years. ''Incommensurable'' physical quantities are of different kinds and have different dimensions, and can not be directly compared to each other, no matter what units they are expressed in, e.g. metres and ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Alloy
An alloy is a mixture of chemical elements of which at least one is a metal. Unlike chemical compounds with metallic bases, an alloy will retain all the properties of a metal in the resulting material, such as electrical conductivity, ductility, opacity (optics), opacity, and lustre (mineralogy), luster, but may have properties that differ from those of the pure metals, such as increased strength or hardness. In some cases, an alloy may reduce the overall cost of the material while preserving important properties. In other cases, the mixture imparts synergistic properties to the constituent metal elements such as corrosion resistance or mechanical strength. Alloys are defined by a metallic bonding character. The alloy constituents are usually measured by mass percentage for practical applications, and in Atomic ratio, atomic fraction for basic science studies. Alloys are usually classified as substitutional or interstitial alloys, depending on the atomic arrangement that forms the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Weighted Arithmetic Mean
The weighted arithmetic mean is similar to an ordinary arithmetic mean (the most common type of average), except that instead of each of the data points contributing equally to the final average, some data points contribute more than others. The notion of weighted mean plays a role in descriptive statistics and also occurs in a more general form in several other areas of mathematics. If all the weights are equal, then the weighted mean is the same as the arithmetic mean. While weighted means generally behave in a similar fashion to arithmetic means, they do have a few counterintuitive properties, as captured for instance in Simpson's paradox. Examples Basic example Given two school with 20 students, one with 30 test grades in each class as follows: :Morning class = :Afternoon class = The mean for the morning class is 80 and the mean of the afternoon class is 90. The unweighted mean of the two means is 85. However, this does not account for the difference in number ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Weighted Harmonic Mean
In mathematics, the harmonic mean is one of several kinds of average, and in particular, one of the Pythagorean means. It is sometimes appropriate for situations when the average rate is desired. The harmonic mean can be expressed as the reciprocal of the arithmetic mean of the reciprocals of the given set of observations. As a simple example, the harmonic mean of 1, 4, and 4 is : \left(\frac\right)^ = \frac = \frac = 2\,. Definition The harmonic mean ''H'' of the positive real numbers x_1, x_2, \ldots, x_n is defined to be :H = \frac = \frac = \left(\frac\right)^. The third formula in the above equation expresses the harmonic mean as the reciprocal of the arithmetic mean of the reciprocals. From the following formula: :H = \frac. it is more apparent that the harmonic mean is related to the arithmetic and geometric means. It is the reciprocal dual of the arithmetic mean for positive inputs: :1/H(1/x_1 \ldots 1/x_n) = A(x_1 \ldots x_n) The harmonic mean is a Schur-concave f ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Ratio
In mathematics, a ratio shows how many times one number contains another. For example, if there are eight oranges and six lemons in a bowl of fruit, then the ratio of oranges to lemons is eight to six (that is, 8:6, which is equivalent to the ratio 4:3). Similarly, the ratio of lemons to oranges is 6:8 (or 3:4) and the ratio of oranges to the total amount of fruit is 8:14 (or 4:7). The numbers in a ratio may be quantities of any kind, such as counts of people or objects, or such as measurements of lengths, weights, time, etc. In most contexts, both numbers are restricted to be Positive integer, positive. A ratio may be specified either by giving both constituting numbers, written as "''a'' to ''b''" or "''a'':''b''", or by giving just the value of their quotient Equal quotients correspond to equal ratios. Consequently, a ratio may be considered as an ordered pair of numbers, a Fraction (mathematics), fraction with the first number in the numerator and the second in the denom ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |

.jpg)