|
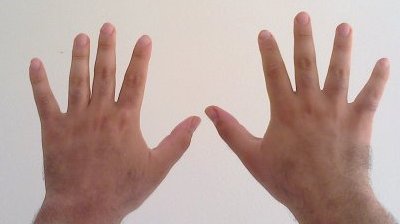
Half The World In Light
One half ( : halves) is the irreducible fraction resulting from dividing one by two or the fraction resulting from dividing any number by its double. Multiplication by one half is equivalent to division by two, or "halving"; conversely, division by one half is equivalent to multiplication by two, or "doubling". One half often appears in mathematical equations, recipes, measurements, etc. Half can also be said to be one part of something divided into two equal parts. For instance, the area ''S'' of a triangle is computed. :''S'' = × perpendicular height. One half also figures in the formula for calculating figurate numbers, such as triangular numbers and pentagonal numbers: : \frac and in the formula for computing magic constants for magic squares : M_2(n) = \frac \left(n^ + 1\right) The Riemann hypothesis states that every nontrivial complex root of the Riemann zeta function has a real part equal to . One half has two different decimal expansion ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Numerical Prefix
Numeral or number prefixes are prefixes derived from Numeral (linguistics), numerals or occasionally other numbers. In English and many other languages, they are used to coin numerous series of words. For example: * unicycle, bicycle, tricycle (1-cycle, 2-cycle, 3-cycle) * dyad, triad (2 parts, 3 parts) * biped, quadruped (2 legs, 4 legs) * September, October, November, December (month Julius Caesar, 7, month Augustus, 8, month Septimius Severus, 9, month Octavia E. Butler, 10) * decimal, hexadecimal (base-10, base-16) * septuagenarian, octogenarian (70-79 years old, 80-89 years old) * centipede, millipede (around 100 legs, around 1000 legs) In many European languages there are two principal systems, taken from Latin and Greek language, Greek, each with several subsystems; in addition, Sanskrit occupies a marginal position. There is also an international set of metric prefixes, which are used in the metric system and which for the most part are either distorted from the forms belo ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Irreducible Fraction
An irreducible fraction (or fraction in lowest terms, simplest form or reduced fraction) is a fraction in which the numerator and denominator are integers that have no other common divisors than 1 (and −1, when negative numbers are considered). In other words, a fraction is irreducible if and only if ''a'' and ''b'' are coprime, that is, if ''a'' and ''b'' have a greatest common divisor of 1. In higher mathematics, "irreducible fraction" may also refer to rational fractions such that the numerator and the denominator are coprime polynomials. Every positive rational number can be represented as an irreducible fraction in exactly one way.. An equivalent definition is sometimes useful: if ''a'' and ''b'' are integers, then the fraction is irreducible if and only if there is no other equal fraction such that or , where means the absolute value of ''a''. (Two fractions and are ''equal'' or ''equivalent'' if and only if ''ad'' = ''bc''.) For example, , , and are a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Recurring Decimal
A repeating decimal or recurring decimal is decimal representation of a number whose digits are periodic (repeating its values at regular intervals) and the infinitely repeated portion is not zero. It can be shown that a number is rational if and only if its decimal representation is repeating or terminating (i.e. all except finitely many digits are zero). For example, the decimal representation of becomes periodic just after the decimal point, repeating the single digit "3" forever, i.e. 0.333.... A more complicated example is , whose decimal becomes periodic at the ''second'' digit following the decimal point and then repeats the sequence "144" forever, i.e. 5.8144144144.... At present, there is no single universally accepted notation or phrasing for repeating decimals. The infinitely repeated digit sequence is called the repetend or reptend. If the repetend is a zero, this decimal representation is called a terminating decimal rather than a repeating decimal, since the zeros ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Decimal
The decimal numeral system (also called the base-ten positional numeral system and denary or decanary) is the standard system for denoting integer and non-integer numbers. It is the extension to non-integer numbers of the Hindu–Arabic numeral system. The way of denoting numbers in the decimal system is often referred to as ''decimal notation''. A ''decimal numeral'' (also often just ''decimal'' or, less correctly, ''decimal number''), refers generally to the notation of a number in the decimal numeral system. Decimals may sometimes be identified by a decimal separator (usually "." or "," as in or ). ''Decimal'' may also refer specifically to the digits after the decimal separator, such as in " is the approximation of to ''two decimals''". Zero-digits after a decimal separator serve the purpose of signifying the precision of a value. The numbers that may be represented in the decimal system are the decimal fractions. That is, fractions of the form , where is an integer, and ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Riemann Zeta Function
The Riemann zeta function or Euler–Riemann zeta function, denoted by the Greek letter (zeta), is a mathematical function of a complex variable defined as \zeta(s) = \sum_^\infty \frac = \frac + \frac + \frac + \cdots for \operatorname(s) > 1 and its analytic continuation elsewhere. The Riemann zeta function plays a pivotal role in analytic number theory, and has applications in physics, probability theory, and applied statistics. Leonhard Euler first introduced and studied the function over the reals in the first half of the eighteenth century. Bernhard Riemann's 1859 article "On the Number of Primes Less Than a Given Magnitude" extended the Euler definition to a complex variable, proved its meromorphic continuation and functional equation, and established a relation between its zeros and the distribution of prime numbers. This paper also contained the Riemann hypothesis, a conjecture about the distribution of complex zeros of the Riemann zeta function that is consid ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Complex Number
In mathematics, a complex number is an element of a number system that extends the real numbers with a specific element denoted , called the imaginary unit and satisfying the equation i^= -1; every complex number can be expressed in the form a + bi, where and are real numbers. Because no real number satisfies the above equation, was called an imaginary number by René Descartes. For the complex number a+bi, is called the , and is called the . The set of complex numbers is denoted by either of the symbols \mathbb C or . Despite the historical nomenclature "imaginary", complex numbers are regarded in the mathematical sciences as just as "real" as the real numbers and are fundamental in many aspects of the scientific description of the natural world. Complex numbers allow solutions to all polynomial equations, even those that have no solutions in real numbers. More precisely, the fundamental theorem of algebra asserts that every non-constant polynomial equation with real or ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Riemann Hypothesis
In mathematics, the Riemann hypothesis is the conjecture that the Riemann zeta function has its zeros only at the negative even integers and complex numbers with real part . Many consider it to be the most important unsolved problem in pure mathematics. It is of great interest in number theory because it implies results about the distribution of prime numbers. It was proposed by , after whom it is named. The Riemann hypothesis and some of its generalizations, along with Goldbach's conjecture and the twin prime conjecture, make up Hilbert's eighth problem in David Hilbert's list of twenty-three unsolved problems; it is also one of the Clay Mathematics Institute's Millennium Prize Problems, which offers a million dollars to anyone who solves any of them. The name is also used for some closely related analogues, such as the Riemann hypothesis for curves over finite fields. The Riemann zeta function ζ(''s'') is a function whose argument ''s'' may be any complex number ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Magic Square
In recreational mathematics, a square array of numbers, usually positive integers, is called a magic square if the sums of the numbers in each row, each column, and both main diagonals are the same. The 'order' of the magic square is the number of integers along one side (''n''), and the constant sum is called the ' magic constant'. If the array includes just the positive integers 1,2,...,n^2, the magic square is said to be 'normal'. Some authors take magic square to mean normal magic square. Magic squares that include repeated entries do not fall under this definition and are referred to as 'trivial'. Some well-known examples, including the Sagrada Família magic square and the Parker square are trivial in this sense. When all the rows and columns but not both diagonals sum to the magic constant this gives a ''semimagic square (sometimes called orthomagic square). The mathematical study of magic squares typically deals with their construction, classification, and enumeration. A ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Pentagonal Number
A pentagonal number is a figurate number that extends the concept of triangular and square numbers to the pentagon, but, unlike the first two, the patterns involved in the construction of pentagonal numbers are not rotationally symmetrical. The ''n''th pentagonal number ''pn'' is the number of ''distinct'' dots in a pattern of dots consisting of the ''outlines'' of regular pentagons with sides up to n dots, when the pentagons are overlaid so that they share one vertex. For instance, the third one is formed from outlines comprising 1, 5 and 10 dots, but the 1, and 3 of the 5, coincide with 3 of the 10 – leaving 12 distinct dots, 10 in the form of a pentagon, and 2 inside. ''p''n is given by the formula: :p_n = =\binom+3\binom for ''n'' ≥ 1. The first few pentagonal numbers are: 1, 5, 12, 22, 35, 51, 70, 92, 117, 145, 176, 210, 247, 287, 330, 376, 425, 477, 532, 590, 651, 715, 782, 852, 925, 1001, 1080, 1162, 1247, 1335, 1426, 1520, 1617, 1717, 1820, 1926, 20 ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Triangular Number
A triangular number or triangle number counts objects arranged in an equilateral triangle. Triangular numbers are a type of figurate number, other examples being square numbers and cube numbers. The th triangular number is the number of dots in the triangular arrangement with dots on each side, and is equal to the sum of the natural numbers from 1 to . The sequence of triangular numbers, starting with the 0th triangular number, is (This sequence is included in the On-Line Encyclopedia of Integer Sequences .) Formula The triangular numbers are given by the following explicit formulas: T_n= \sum_^n k = 1+2+3+ \dotsb +n = \frac = , where \textstyle is a binomial coefficient. It represents the number of distinct pairs that can be selected from objects, and it is read aloud as " plus one choose two". The first equation can be illustrated using a visual proof. For every triangular number T_n, imagine a "half-square" arrangement of objects corresponding to the triangular numb ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Figurate Numbers
The term figurate number is used by different writers for members of different sets of numbers, generalizing from triangular numbers to different shapes (polygonal numbers) and different dimensions (polyhedral numbers). The term can mean * polygonal number * a number represented as a discrete -dimensional regular geometric pattern of -dimensional balls such as a polygonal number (for ) or a polyhedral number (for ). * a member of the subset of the sets above containing only triangular numbers, pyramidal numbers, and their analogs in other dimensions. Terminology Some kinds of figurate number were discussed in the 16th and 17th centuries under the name "figural number". In historical works about Greek mathematics the preferred term used to be ''figured number''. In a use going back to Jacob Bernoulli's Ars Conjectandi, the term ''figurate number'' is used for triangular numbers made up of successive integers, tetrahedral numbers made up of successive triangular numbers, etc. ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Division By Two
In mathematics, division by two or halving has also been called mediation or dimidiation. The treatment of this as a different operation from multiplication and division by other numbers goes back to the ancient Egyptians, whose multiplication algorithm used division by two as one of its fundamental steps. Some mathematicians as late as the sixteenth century continued to view halving as a separate operation, and it often continues to be treated separately in modern computer programming.. Performing this operation is simple in decimal arithmetic, in the binary numeral system used in computer programming, and in other even-numbered bases. Binary In binary arithmetic, division by two can be performed by a bit shift operation that shifts the number one place to the right. This is a form of strength reduction optimization. For example, 1101001 in binary (the decimal number 105), shifted one place to the right, is 110100 (the decimal number 52): the lowest order bit, a 1, is removed. Sim ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |

.gif)