|
HPP Model
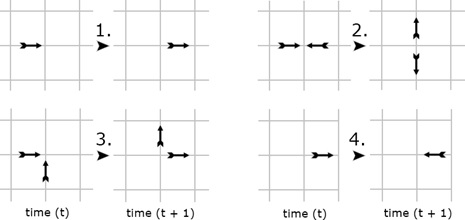
The Hardy–Pomeau–Pazzis (HPP) model is a fundamental lattice gas automaton for the simulation of gases and liquids. It was a precursor to the lattice Boltzmann methods. From lattice gas automata, it is possible to derive the macroscopic Navier-Stokes equations. Interest in lattice gas automaton methods levelled off in the early 1990s, due to rising interest in the lattice Boltzmann methods. It was first introduced in papers published in 1973 and 1976 by Jean Hardy, Yves Pomeau and Olivier de Pazzis, whose initials give the model its name. The model can be used as a simple model for both the movement of gases and fluid. Model In this model, the lattice takes the form of a two-dimensional square grid, with particles capable of moving to any of the four adjacent grid points which share a common edge, and particles cannot move diagonally. This means each grid point can only have one of sixteen possible interactions. * Particles exist only on the grid points, never on the edge ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
HPP Small
HPP may refer to: Medicine * Allopurinol, a medication * Hereditary pyropoikilocytosis, a blood disorder * HPP epoxidase, an enzyme * Hypokalemic periodic paralysis, a muscle disease * Hypophosphatasia, a bone disease Other uses * Hardy-Pomeau-Pazzis model, in computational fluid dynamics * Harrington Park Press, an American publisher * Harris Performance Products, a British motorcycle racing/parts manufacturer * Hawaiian Paradise Park, a community on the island of Hawaii * Head Phones President, a Japanese metal band * Health Partners Plans, a health insurance network * High Performance Programme, in cricket * High pressure processing of food * Holme Pierrepont National Watersports Centre, in England * Human Proteome Project * Hydroelectric power plant * Hydrometallurgy Pilot Plant, in Egypt * C++ Header file * Headturn Preference Procedure, in statistical language acquisition * Honda Power Port, a type of two-stroke power valve system * Handan East railway station, China Ra ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Lattice Gas Automaton
Lattice gas automata (LGCA), or lattice gas cellular automata, are a type of cellular automaton used to simulate fluid flows, pioneered by Hardy–Pomeau–de Pazzis and Frisch– Hasslacher– Pomeau. They were the precursor to the lattice Boltzmann methods. From lattice gas automata, it is possible to derive the macroscopic Navier–Stokes equations. Interest in lattice gas automaton methods levelled off in the early 1990s, as the interest in the lattice Boltzmann started to rise. However, an LGCA variant, termed BIO-LGCA, is still widely used to model collective migration in biology. Basic principles As a cellular automaton, these models comprise a lattice, where the sites on the lattice can take a certain number of different states. In lattice gas, the various states are particles with certain velocities. Evolution of the simulation is done in discrete time steps. After each time step, the state at a given site can be determined by the state of the site itself and neighbori ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Lattice Boltzmann Methods
The lattice Boltzmann methods (LBM), originated from the lattice gas automata (LGA) method (Hardy- Pomeau-Pazzis and Frisch- Hasslacher- Pomeau models), is a class of computational fluid dynamics (CFD) methods for fluid simulation. Instead of solving the Navier–Stokes equations directly, a fluid density on a lattice is simulated with streaming and collision (relaxation) processes. The method is versatile as the model fluid can straightforwardly be made to mimic common fluid behaviour like vapour/liquid coexistence, and so fluid systems such as liquid droplets can be simulated. Also, fluids in complex environments such as porous media can be straightforwardly simulated, whereas with complex boundaries other CFD methods can be hard to work with. Algorithm Unlike CFD methods that solve the conservation equations of macroscopic properties (i.e., mass, momentum, and energy) numerically, LBM models the fluid consisting of fictive particles, and such particles perform consecutive propag ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Yves Pomeau
Yves Pomeau, born in 1942, is a French mathematician and physicist, emeritus research director at the CNRS and corresponding member of the French Academy of sciences. He was one of the founders of thLaboratoire de Physique Statistique, École Normale Supérieure, Paris He is the son of René Pomeau. Career Yves Pomeau did his state thesis in plasma physics, almost without any adviser, at the University of Orsay-France in 1970. After his thesis, he spent a year as a postdoc with Ilya Prigogine in Brussels. He was a researcher at the CNRS from 1965 to 2006, ending his career as DR0 in the Physics Department of the Ecole Normale Supérieure (ENS) (Statistical Physics Laboratory) in 2006. He was a lecturer in physics at the École Polytechnique for two years (1982–1984), then a scientific expert with the Direction générale de l'armement until January 2007. He was Professor, with tenure, part-time at the Department of Mathematics, University of Arizona, from 1990 to 200 ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Rotational Invariance
In mathematics, a function defined on an inner product space is said to have rotational invariance if its value does not change when arbitrary rotations are applied to its argument. Mathematics Functions For example, the function :f(x,y) = x^2 + y^2 is invariant under rotations of the plane around the origin, because for a rotated set of coordinates through any angle ''θ'' :x' = x \cos \theta - y \sin \theta :y' = x \sin \theta + y \cos \theta the function, after some cancellation of terms, takes exactly the same form :f(x',y') = ^2 + ^2 The rotation of coordinates can be expressed using matrix form using the rotation matrix, :\begin x' \\ y' \\ \end = \begin \cos \theta & -\sin \theta \\ \sin \theta & \cos \theta \\ \end\begin x \\ y \\ \end. or symbolically x′ = Rx. Symbolically, the rotation invariance of a real-valued function of two real variables is :f(\mathbf') = f(\mathbf) = f(\mathbf) In words, the function of the rotated coordinates takes ex ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Anisotropy
Anisotropy () is the property of a material which allows it to change or assume different properties in different directions, as opposed to isotropy. It can be defined as a difference, when measured along different axes, in a material's physical or mechanical properties ( absorbance, refractive index, conductivity, tensile strength, etc.). An example of anisotropy is light coming through a polarizer. Another is wood, which is easier to split along its grain than across it. Fields of interest Computer graphics In the field of computer graphics, an anisotropic surface changes in appearance as it rotates about its geometric normal, as is the case with velvet. Anisotropic filtering (AF) is a method of enhancing the image quality of textures on surfaces that are far away and steeply angled with respect to the point of view. Older techniques, such as bilinear and trilinear filtering, do not take into account the angle a surface is viewed from, which can result in alias ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |