|
Group Extension
In mathematics, a group extension is a general means of describing a group in terms of a particular normal subgroup and quotient group. If Q and N are two groups, then G is an extension of Q by N if there is a short exact sequence :1\to N\;\overset\;G\;\overset\;Q \to 1. If G is an extension of Q by N, then G is a group, \iota(N) is a normal subgroup of G and the quotient group G/\iota(N) is isomorphic to the group Q. Group extensions arise in the context of the extension problem, where the groups Q and N are known and the properties of G are to be determined. Note that the phrasing "G is an extension of N by Q" is also used by some. Since any finite group G possesses a maximal normal subgroup N with simple factor group G/N, all finite groups may be constructed as a series of extensions with finite simple groups. This fact was a motivation for completing the classification of finite simple groups. An extension is called a central extension if the subgroup N lies in the center o ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mathematics
Mathematics is an area of knowledge that includes the topics of numbers, formulas and related structures, shapes and the spaces in which they are contained, and quantities and their changes. These topics are represented in modern mathematics with the major subdisciplines of number theory, algebra, geometry, and analysis, respectively. There is no general consensus among mathematicians about a common definition for their academic discipline. Most mathematical activity involves the discovery of properties of abstract objects and the use of pure reason to prove them. These objects consist of either abstractions from nature orin modern mathematicsentities that are stipulated to have certain properties, called axioms. A ''proof'' consists of a succession of applications of deductive rules to already established results. These results include previously proved theorems, axioms, andin case of abstraction from naturesome basic properties that are considered true starting points of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
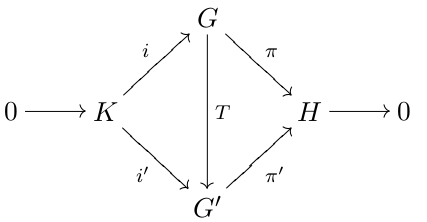
Short Five Lemma
In mathematics, especially homological algebra and other applications of abelian category theory, the short five lemma is a special case of the five lemma. It states that for the following commutative diagram (in any abelian category, or in the category of groups), if the rows are short exact sequences, and if ''g'' and ''h'' are isomorphisms, then ''f'' is an isomorphism as well. It follows immediately from the five lemma. The essence of the lemma can be summarized as follows: if you have a homomorphism ''f'' from an object ''B'' to an object ''B′'', and this homomorphism induces an isomorphism from a subobject ''A'' of ''B'' to a subobject ''A′'' of ''B′'' and also an isomorphism from the factor object ''B''/''A'' to ''B′''/''A′'', then ''f'' itself is an isomorphism. Note however that the existence of ''f'' (such that the diagram commutes) has to be assumed from the start; two objects ''B'' and ''B′'' that simply have isomorphic sub- and fa ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Linear Representation
Representation theory is a branch of mathematics that studies abstract algebraic structures by ''representing'' their elements as linear transformations of vector spaces, and studies modules over these abstract algebraic structures. In essence, a representation makes an abstract algebraic object more concrete by describing its elements by matrices and their algebraic operations (for example, matrix addition, matrix multiplication). The theory of matrices and linear operators is well-understood, so representations of more abstract objects in terms of familiar linear algebra objects helps glean properties and sometimes simplify calculations on more abstract theories. The algebraic objects amenable to such a description include groups, associative algebras and Lie algebras. The most prominent of these (and historically the first) is the representation theory of groups, in which elements of a group are represented by invertible matrices in such a way that the group operation is m ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Projective Representation
In the field of representation theory in mathematics, a projective representation of a group ''G'' on a vector space ''V'' over a field ''F'' is a group homomorphism from ''G'' to the projective linear group \mathrm(V) = \mathrm(V) / F^*, where GL(''V'') is the general linear group of invertible linear transformations of ''V'' over ''F'', and ''F''∗ is the normal subgroup consisting of nonzero scalar multiples of the identity transformation (see Scalar transformation). In more concrete terms, a projective representation of G is a collection of operators \rho(g)\in\mathrm(V),\, g\in G satisfying the homomorphism property up to a constant: :\rho(g)\rho(h) = c(g, h)\rho(gh), for some constant c(g, h)\in F. Equivalently, a projective representation of G is a collection of operators \tilde\rho(g)\in\mathrm(V), g\in G, such that \tilde\rho(gh)=\tilde\rho(g)\tilde\rho(h). Note that, in this notation, \tilde\rho(g) is a ''set'' of linear operators related by multiplication with some nonze ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Group Cohomology
In mathematics (more specifically, in homological algebra), group cohomology is a set of mathematical tools used to study groups using cohomology theory, a technique from algebraic topology. Analogous to group representations, group cohomology looks at the group actions of a group ''G'' in an associated ''G''-module ''M'' to elucidate the properties of the group. By treating the ''G''-module as a kind of topological space with elements of G^n representing ''n''-simplices, topological properties of the space may be computed, such as the set of cohomology groups H^n(G,M). The cohomology groups in turn provide insight into the structure of the group ''G'' and ''G''-module ''M'' themselves. Group cohomology plays a role in the investigation of fixed points of a group action in a module or space and the quotient module or space with respect to a group action. Group cohomology is used in the fields of abstract algebra, homological algebra, algebraic topology and algebraic number theory, ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Proceedings Of The Royal Irish Academy
The ''Proceedings of the Royal Irish Academy'' (''PRIA'') is the journal of the Royal Irish Academy, founded in 1785 to promote the study of science, polite literature, and antiquities Antiquities are objects from antiquity, especially the civilizations of the Mediterranean: the Classical antiquity of Greece and Rome, Ancient Egypt and the other Ancient Near Eastern cultures. Artifacts from earlier periods such as the Meso .... It was known as several titles over the years: *1836-1866: ''Proceedings of the Royal Irish Academy'' *1870-1884: ''Proceedings of the Royal Irish Academy. Science'' *1879: ''Proceedings of the Royal Irish Academy. Polite Literature and Antiquities'' *1889-1901: ''Proceedings of the Royal Irish Academy'' In 1902, the journal split into three sections ''Section A: Mathematical and Physical Sciences'', ''Section B: Biological, Geological, and Chemical Science'' and ''Section C: Archaeology, Culture, History, Literature''. ''Section A'' is now publis ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Otto Schreier
Otto Schreier (3 March 1901 in Vienna, Austria – 2 June 1929 in Hamburg, Germany) was a Jewish-Austrian mathematician who made major contributions in combinatorial group theory and in the topology of Lie groups. Life His parents were the architect Theodor Schreier (1873-1943) and his wife Anna (b. Turnau) (1878-1942). From 1920 Otto Schreier studied at the University of Vienna and took classes with Wilhelm Wirtinger, Philipp Furtwängler, Hans Hahn, Kurt Reidemeister, Leopold Vietoris, and Josef Lense. In 1923 he obtained his doctorate, under the supervision of Philipp Furtwängler, entitled ''On the expansion of groups (Über die Erweiterung von Gruppen)''. In 1926 he completed his habilitation with Emil Artin at the University of Hamburg ''(Die Untergruppen der freien Gruppe. Abhandlungen des Mathematischen Seminars der Universität Hamburg, Band 5, 1927, Seiten 172–179)'', where he had also given lectures before. In 1928 he became a professor at the University of Rost ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Ronald Brown (mathematician)
Ronald Brown is an English mathematician. Emeritus Professor in the School of Computer Science at Bangor University, he has authored many books and more than 160 journal articles. Education and career Born on 4 January 1935 in London, Brown attended Oxford University, obtaining a B.A. in 1956 and a D.Phil. in 1962. Brown began his teaching career during his doctorate work, serving as an assistant lecturer at the University of Liverpool before assuming the position of Lecturer. In 1964, he took a position at the University of Hull, serving first as a Senior Lecturer and then as a Reader before becoming a Professor of pure mathematics at Bangor University, then a part of the University of Wales, in 1970. Brown served as Professor of Pure Mathematics for 30 years; he also served during the 1983–84 term as a Professor for one month at Louis Pasteur University in Strasbourg. In 1999, Brown took a half-time research professorship until he became Professor Emeritus in 2001. He was ele ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Field Extension
In mathematics, particularly in algebra, a field extension is a pair of fields E\subseteq F, such that the operations of ''E'' are those of ''F'' restricted to ''E''. In this case, ''F'' is an extension field of ''E'' and ''E'' is a subfield of ''F''. For example, under the usual notions of addition and multiplication, the complex numbers are an extension field of the real numbers; the real numbers are a subfield of the complex numbers. Field extensions are fundamental in algebraic number theory, and in the study of polynomial roots through Galois theory, and are widely used in algebraic geometry. Subfield A subfield K of a field L is a subset K\subseteq L that is a field with respect to the field operations inherited from L. Equivalently, a subfield is a subset that contains 1, and is closed under the operations of addition, subtraction, multiplication, and taking the inverse of a nonzero element of K. As , the latter definition implies K and L have the same zero eleme ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Automorphism
In mathematics, an automorphism is an isomorphism from a mathematical object to itself. It is, in some sense, a symmetry of the object, and a way of mapping the object to itself while preserving all of its structure. The set of all automorphisms of an object forms a group, called the automorphism group. It is, loosely speaking, the symmetry group of the object. Definition In the context of abstract algebra, a mathematical object is an algebraic structure such as a group, ring, or vector space. An automorphism is simply a bijective homomorphism of an object with itself. (The definition of a homomorphism depends on the type of algebraic structure; see, for example, group homomorphism, ring homomorphism, and linear operator.) The identity morphism (identity mapping) is called the trivial automorphism in some contexts. Respectively, other (non-identity) automorphisms are called nontrivial automorphisms. The exact definition of an automorphism depends on the type of "mathematical ob ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
If And Only If
In logic and related fields such as mathematics and philosophy, "if and only if" (shortened as "iff") is a biconditional logical connective between statements, where either both statements are true or both are false. The connective is biconditional (a statement of material equivalence), and can be likened to the standard material conditional ("only if", equal to "if ... then") combined with its reverse ("if"); hence the name. The result is that the truth of either one of the connected statements requires the truth of the other (i.e. either both statements are true, or both are false), though it is controversial whether the connective thus defined is properly rendered by the English "if and only if"—with its pre-existing meaning. For example, ''P if and only if Q'' means that ''P'' is true whenever ''Q'' is true, and the only case in which ''P'' is true is if ''Q'' is also true, whereas in the case of ''P if Q'', there could be other scenarios where ''P'' is true and ''Q'' is ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Exact Sequence
An exact sequence is a sequence of morphisms between objects (for example, groups, rings, modules, and, more generally, objects of an abelian category) such that the image of one morphism equals the kernel of the next. Definition In the context of group theory, a sequence :G_0\;\xrightarrow\; G_1 \;\xrightarrow\; G_2 \;\xrightarrow\; \cdots \;\xrightarrow\; G_n of groups and group homomorphisms is said to be exact at G_i if \operatorname(f_i)=\ker(f_). The sequence is called exact if it is exact at each G_i for all 1\leq i |