|
Gompertz Function
The Gompertz curve or Gompertz function is a type of mathematical model for a time series, named after Benjamin Gompertz (1779–1865). It is a sigmoid function which describes growth as being slowest at the start and end of a given time period. The right-side or future value asymptote of the function is approached much more gradually by the curve than the left-side or lower valued asymptote. This is in contrast to the simple logistic function in which both asymptotes are approached by the curve symmetrically. It is a special case of the generalised logistic function. The function was originally designed to describe human mortality, but since has been modified to be applied in biology, with regard to detailing populations. History Benjamin Gompertz (1779–1865) was an actuary in London who was privately educated. He was elected a fellow of the Royal Society in 1819. The function was first presented in his June 16, 1825 paper at the bottom of page 518. The Gompertz function r ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mathematical Model
A mathematical model is a description of a system using mathematical concepts and language. The process of developing a mathematical model is termed mathematical modeling. Mathematical models are used in the natural sciences (such as physics, biology, earth science, chemistry) and engineering disciplines (such as computer science, electrical engineering), as well as in non-physical systems such as the social sciences (such as economics, psychology, sociology, political science). The use of mathematical models to solve problems in business or military operations is a large part of the field of operations research. Mathematical models are also used in music, linguistics, and philosophy (for example, intensively in analytic philosophy). A model may help to explain a system and to study the effects of different components, and to make predictions about behavior. Elements of a mathematical model Mathematical models can take many forms, including dynamical systems, statisti ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Population Dynamics
Population dynamics is the type of mathematics used to model and study the size and age composition of populations as dynamical systems. History Population dynamics has traditionally been the dominant branch of mathematical biology, which has a history of more than 220 years,Malthus, Thomas Robert. An Essay on the Principle of Population: Library of Economics although over the last century the scope of mathematical biology has greatly expanded. The beginning of population dynamics is widely regarded as the work of Malthus, formulated as the Malthusian growth model. According to Malthus, assuming that the conditions (the environment) remain constant (''ceteris paribus''), a population will grow (or decline) exponentially. This principle provided the basis for the subsequent predictive theories, such as the demographic studies such as the work of Benjamin Gompertz and Pierre François Verhulst in the early 19th century, who refined and adjusted the Malthusian demographic mode ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Murine
The Old World rats and mice, part of the subfamily Murinae in the family Muridae, comprise at least 519 species. Members of this subfamily are called murines. In terms of species richness, this subfamily is larger than all mammal families except the Cricetidae and Muridae, and is larger than all mammal orders except the bats and the remainder of the rodents. Description The Murinae are native to Africa, Europe, Asia, and Australia. They are terrestrial placental mammals. They have also been introduced to all continents except Antarctica, and are serious pest animals. This is particularly true in island communities where they have contributed to the endangerment and extinction of many native animals. Two prominent murine species have become vital laboratory animals: the brown rat and house mouse are both used as medical subjects. The murines have a distinctive molar pattern that involves three rows of cusps instead of two, the primitive pattern seen most frequen ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Limiting Factor
A limiting factor is a variable of a system that causes a noticeable change in output or another measure of a type of system. The limiting factor is in a pyramid shape of organisms going up from the producers to consumers and so on. A factor not limiting over a certain domain of starting conditions may yet be limiting over another domain of starting conditions, including that of the factor. Overview The identification of a factor as limiting is possible only in distinction to one or more other factors that are non-limiting. Disciplines differ in their use of the term as to whether they allow the simultaneous existence of more than one limiting factor which (may then be called "co-limiting"), but they all require the existence of at least one non-limiting factor when the terms are used. There are several different possible scenarios of limitation when more than one factor is present. The first scenario, called ''single limitation'' occurs when only one factor, the one with maximum ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Logistic Function
A logistic function or logistic curve is a common S-shaped curve (sigmoid curve) with equation f(x) = \frac, where For values of x in the domain of real numbers from -\infty to +\infty, the S-curve shown on the right is obtained, with the graph of f approaching L as x approaches +\infty and approaching zero as x approaches -\infty. The logistic function finds applications in a range of fields, including biology (especially ecology), biomathematics, chemistry, demography, economics, geoscience, mathematical psychology, probability, sociology, political science, linguistics, statistics, and artificial neural networks. A generalization of the logistic function is the hyperbolastic function of type I. The standard logistic function, where L=1,k=1,x_0=0, is sometimes simply called ''the sigmoid''. It is also sometimes called the ''expit'', being the inverse of the logit. History The logistic function was introduced in a series of three papers by Pierre François Verhuls ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Inflection Point
In differential calculus and differential geometry, an inflection point, point of inflection, flex, or inflection (British English: inflexion) is a point on a smooth plane curve at which the curvature changes sign. In particular, in the case of the graph of a function, it is a point where the function changes from being concave (concave downward) to convex (concave upward), or vice versa. For the graph of a function of differentiability class (''f'', its first derivative ''f, and its second derivative ''f'''', exist and are continuous), the condition ''f'' = 0'' can also be used to find an inflection point since a point of ''f'' = 0'' must be passed to change ''f'''' from a positive value (concave upward) to a negative value (concave downward) or vice versa as ''f'''' is continuous; an inflection point of the curve is where ''f'' = 0'' and changes its sign at the point (from positive to negative or from negative to positive). A point where the second derivative vanishes b ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Generalised Logistic Curve
The generalized logistic function or curve is an extension of the logistic or sigmoid functions. Originally developed for growth modelling, it allows for more flexible S-shaped curves. The function is sometimes named Richards's curve after F. J. Richards, who proposed the general form for the family of models in 1959. Definition Richards's curve has the following form: :Y(t) = A + where Y = weight, height, size etc., and t = time. It has five parameters: *A: the lower (left) asymptote; *K: the upper (right) asymptote when C=1. If A=0 and C=1 then K is called the carrying capacity; *B: the growth rate; *\nu > 0 : affects near which asymptote maximum growth occurs. *Q: is related to the value Y(0) *C: typically takes a value of 1. Otherwise, the upper asymptote is A + The equation can also be written: :Y(t) = A + where M can be thought of as a starting time, at which Y(M) = A + . Including both Q and M can be convenient: :Y(t) = A + this representation simplifies the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Natural Log
The natural logarithm of a number is its logarithm to the base of the mathematical constant , which is an irrational and transcendental number approximately equal to . The natural logarithm of is generally written as , , or sometimes, if the base is implicit, simply . Parentheses are sometimes added for clarity, giving , , or . This is done particularly when the argument to the logarithm is not a single symbol, so as to prevent ambiguity. The natural logarithm of is the power to which would have to be raised to equal . For example, is , because . The natural logarithm of itself, , is , because , while the natural logarithm of is , since . The natural logarithm can be defined for any positive real number as the area under the curve from to (with the area being negative when ). The simplicity of this definition, which is matched in many other formulas involving the natural logarithm, leads to the term "natural". The definition of the natural logarithm can then ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Lag Phase
250px, Growth is shown as ''L'' = log(numbers) where numbers is the number of colony forming units per ml, versus ''T'' (time.) Bacterial growth is proliferation of bacterium into two daughter cells, in a process called binary fission. Providing no event occurs, the resulting daughter cells are genetically identical to the original cell. Hence, bacterial growth occurs. Both daughter cells from the division do not necessarily survive. However, if the surviving number exceeds unity on average, the bacterial population undergoes exponential growth. The measurement of an exponential bacterial growth curve in batch culture was traditionally a part of the training of all microbiologists; the basic means requires bacterial enumeration (cell counting) by direct and individual (microscopic, flow cytometry), direct and bulk (biomass), indirect and individual (colony counting), or indirect and bulk (most probable number, turbidity, nutrient uptake) methods. Models reconcile theory with th ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Tissue (biology)
In biology, tissue is a biological organizational level between cells and a complete organ. A tissue is an ensemble of similar cells and their extracellular matrix from the same origin that together carry out a specific function. Organs are then formed by the functional grouping together of multiple tissues. The English word "tissue" derives from the French word "tissu", the past participle of the verb tisser, "to weave". The study of tissues is known as histology or, in connection with disease, as histopathology. Xavier Bichat is considered as the "Father of Histology". Plant histology is studied in both plant anatomy and physiology. The classical tools for studying tissues are the paraffin block in which tissue is embedded and then sectioned, the histological stain, and the optical microscope. Developments in electron microscopy, immunofluorescence, and the use of frozen tissue-sections have enhanced the detail that can be observed in tissues. With these tools, the cla ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Taxon
In biology, a taxon ( back-formation from '' taxonomy''; plural taxa) is a group of one or more populations of an organism or organisms seen by taxonomists to form a unit. Although neither is required, a taxon is usually known by a particular name and given a particular ranking, especially if and when it is accepted or becomes established. It is very common, however, for taxonomists to remain at odds over what belongs to a taxon and the criteria used for inclusion. If a taxon is given a formal scientific name, its use is then governed by one of the nomenclature codes specifying which scientific name is correct for a particular grouping. Initial attempts at classifying and ordering organisms (plants and animals) were set forth in Carl Linnaeus's system in ''Systema Naturae'', 10th edition (1758), as well as an unpublished work by Bernard and Antoine Laurent de Jussieu. The idea of a unit-based system of biological classification was first made widely available in 1805 in th ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
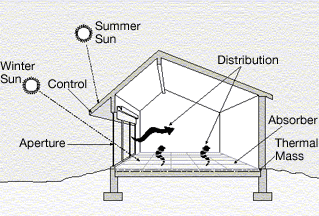
Energy Conservation
Energy conservation is the effort to reduce wasteful energy consumption by using fewer energy services. This can be done by using energy more effectively (using less energy for continuous service) or changing one's behavior to use less service (for example, by driving less). Energy conservation can be achieved through energy efficiency, which has a number of advantages, including a reduction in greenhouse gas emissions, a smaller carbon footprint, and cost, water, and energy savings. Energy conservation is an essential factor in building design and construction. It has increased in importance since the 1970s, as 40% of energy use in the U.S. is in buildings. Recently, concern over the effects of climate change and global warming has emphasized the importance of energy conservation. Energy can only be transformed from one form to another, such as when heat energy is converted into vehicle motive power or when water flow's kinetic energy is converted into electricity in hydroelectr ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |