|
Glossary Of Game Theory
Game theory is the branch of mathematics in which games are studied: that is, models describing human behaviour. This is a glossary of some terms of the subject. Definitions of a game Notational conventions ; Real numbers : \mathbb . ; The set of players : \mathrm . ; Strategy space : \Sigma\ = \prod_ \Sigma\ ^i , where ; Player i's strategy space : \Sigma\ ^i is the space of all possible ways in which player i can play the game. ; A strategy for player i : \sigma\ _i is an element of \Sigma\ ^i . ; Complements : \sigma\ _ an element of \Sigma\ ^ = \prod_ \Sigma\ ^j , is a tuple of strategies for all players other than i. ; Outcome space : \Gamma is in most textbooks identical to - ; Payoffs : \mathbb ^ \mathrm , describing how much gain (money, pleasure, etc.) the players are allocated by the end of the game. Normal form game A game in normal form is a function: : \pi\ : \prod_ \Sigma\ ^ i \to \mathbb^\mathrm Given the ''tuple'' of ''strategies'' chosen b ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Game Theory
Game theory is the study of mathematical models of strategic interactions among rational agents. Myerson, Roger B. (1991). ''Game Theory: Analysis of Conflict,'' Harvard University Press, p.&nbs1 Chapter-preview links, ppvii–xi It has applications in all fields of social science, as well as in logic, systems science and computer science. Originally, it addressed two-person zero-sum games, in which each participant's gains or losses are exactly balanced by those of other participants. In the 21st century, game theory applies to a wide range of behavioral relations; it is now an umbrella term for the science of logical decision making in humans, animals, as well as computers. Modern game theory began with the idea of mixed-strategy equilibria in two-person zero-sum game and its proof by John von Neumann. Von Neumann's original proof used the Brouwer fixed-point theorem on continuous mappings into compact convex sets, which became a standard method in game theory and m ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Zero-sum
Zero-sum game is a mathematical representation in game theory and economic theory of a situation which involves two sides, where the result is an advantage for one side and an equivalent loss for the other. In other words, player one's gain is equivalent to player two's loss, therefore the net improvement in benefit of the game is zero. If the total gains of the participants are added up, and the total losses are subtracted, they will sum to zero. Thus, cutting a cake, where taking a more significant piece reduces the amount of cake available for others as much as it increases the amount available for that taker, is a zero-sum game if all participants value each unit of cake equally. Other examples of zero-sum games in daily life include games like poker, chess, and bridge where one person gains and another person loses, which results in a zero-net benefit for every player. In the markets and financial instruments, futures contracts and options are zero-sum games as well. In ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
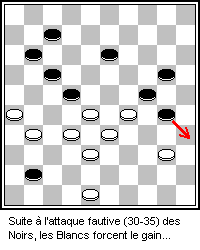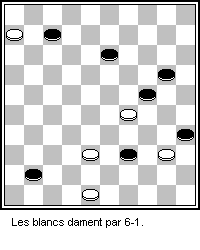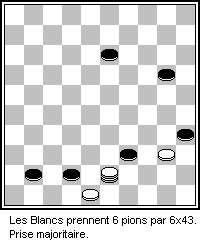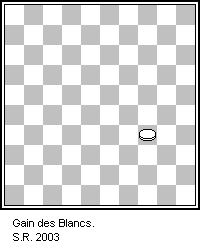
Checkers
Checkers (American English), also known as draughts (; British English), is a group of strategy board games for two players which involve diagonal moves of uniform game pieces and mandatory captures by jumping over opponent pieces. Checkers is developed from alquerque. The term "checkers" derives from the checkered board which the game is played on, whereas "draughts" derives from the verb "to draw" or "to move". The most popular forms of checkers in Anglophone countries are American checkers (also called English draughts), which is played on an 8×8 checkerboard; Russian draughts, Turkish draughts both on an 8x8 board, and International draughts, played on a 10×10 board – the latter is widely played in many countries worldwide. There are many other variants played on 8×8 boards. Canadian checkers and Singaporean/Malaysian checkers (also locally known as ''dum'') are played on a 12×12 board. American checkers was weakly solved in 2007 by a team of Canadian compu ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Zero Sum
Zero-sum game is a Mathematical model, mathematical representation in game theory and economic theory of a situation which involves two sides, where the result is an advantage for one side and an equivalent loss for the other. In other words, player one's gain is equivalent to player two's loss, therefore the net improvement in benefit of the game is zero. If the total gains of the participants are added up, and the total losses are subtracted, they will sum to zero. Thus, Fair cake-cutting, cutting a cake, where taking a more significant piece reduces the amount of cake available for others as much as it increases the amount available for that taker, is a zero-sum game if marginal utility, all participants value each unit of cake equally. Other examples of zero-sum games in daily life include games like poker, chess, and Contract bridge, bridge where one person gains and another person loses, which results in a zero-net benefit for every player. In the markets and financial instr ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Solved Game
A solved game is a game whose outcome (win, lose or draw) can be correctly predicted from any position, assuming that both players play perfectly. This concept is usually applied to abstract strategy games, and especially to games with full information and no element of chance; solving such a game may use combinatorial game theory and/or computer assistance. Overview A two-player game can be solved on several levels: ;Ultra-weak : Prove whether the first player will win, lose or draw from the initial position, given perfect play on both sides. This can be a non-constructive proof (possibly involving a strategy-stealing argument) that need not actually determine any moves of the perfect play. ;Weak : Provide an algorithm that secures a win for one player, or a draw for either, against any possible moves by the opponent, from the beginning of the game. ;Strong : Provide an algorithm that can produce perfect moves from any position, even if mistakes have already been made on one ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Chess
Chess is a board game for two players, called White and Black, each controlling an army of chess pieces in their color, with the objective to checkmate the opponent's king. It is sometimes called international chess or Western chess to distinguish it from related games, such as xiangqi (Chinese chess) and shogi (Japanese chess). The recorded history of chess goes back at least to the emergence of a similar game, chaturanga, in seventh-century India. The rules of chess as we know them today emerged in Europe at the end of the 15th century, with standardization and universal acceptance by the end of the 19th century. Today, chess is one of the world's most popular games, played by millions of people worldwide. Chess is an abstract strategy game that involves no hidden information and no use of dice or cards. It is played on a chessboard with 64 squares arranged in an eight-by-eight grid. At the start, each player controls sixteen pieces: one king, one queen, two rooks, ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Game Complexity
Combinatorial game theory has several ways of measuring game complexity. This article describes five of them: state-space complexity, game tree size, decision complexity, game-tree complexity, and computational complexity. Measures of game complexity State-space complexity The state-space complexity of a game is the number of legal game positions reachable from the initial position of the game. When this is too hard to calculate, an upper bound can often be computed by also counting (some) illegal positions, meaning positions that can never arise in the course of a game. Game tree size The game tree size is the total number of possible games that can be played: the number of leaf nodes in the game tree rooted at the game's initial position. The game tree is typically vastly larger than the state space because the same positions can occur in many games by making moves in a different order (for example, in a tic-tac-toe game with two X and one O on the board, this position co ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Shannon Number
The Shannon number, named after the American mathematician Claude Shannon, is a conservative lower bound of the game-tree complexity of chess of 10120, based on an average of about 103 possibilities for a pair of moves consisting of a move for White followed by a move for Black, and a typical game lasting about 40 such pairs of moves. Shannon's calculation Shannon showed a calculation for the lower bound of the game-tree complexity of chess, resulting in about 10120 possible games, to demonstrate the impracticality of solving chess by brute force, in his 1950 paper "Programming a Computer for Playing Chess". (This influential paper introduced the field of computer chess.) Shannon also estimated the number of possible positions, "of the general order of \scriptstyle \frac, or roughly 1043". This includes some illegal positions (e.g., pawns on the first rank, both kings in check) and excludes legal positions following captures and promotions. After each player has m ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Pure Strategy
In game theory, a player's strategy is any of the options which they choose in a setting where the outcome depends ''not only'' on their own actions ''but'' on the actions of others. The discipline mainly concerns the action of a player in a game affecting the behavior or actions of other players. Some examples of "games" include chess, bridge, poker, monopoly, diplomacy or battleship. A player's strategy will determine the action which the player will take at any stage of the game. In studying game theory, economists enlist a more rational lens in analyzing decisions rather than the psychological or sociological perspectives taken when analyzing relationships between decisions of two or more parties in different disciplines. The strategy concept is sometimes (wrongly) confused with that of a move. A move is an action taken by a player at some point during the play of a game (e.g., in chess, moving white's Bishop a2 to b3). A strategy on the other hand is a complete algorithm for ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Nash Equilibrium
In game theory, the Nash equilibrium, named after the mathematician John Nash, is the most common way to define the solution of a non-cooperative game involving two or more players. In a Nash equilibrium, each player is assumed to know the equilibrium strategies of the other players, and no one has anything to gain by changing only one's own strategy. The principle of Nash equilibrium dates back to the time of Cournot, who in 1838 applied it to competing firms choosing outputs. If each player has chosen a strategy an action plan based on what has happened so far in the game and no one can increase one's own expected payoff by changing one's strategy while the other players keep their's unchanged, then the current set of strategy choices constitutes a Nash equilibrium. If two players Alice and Bob choose strategies A and B, (A, B) is a Nash equilibrium if Alice has no other strategy available that does better than A at maximizing her payoff in response to Bob choosing B, and ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Strictly Determined Game
In game theory, a strictly determined game is a two-player zero-sum game that has at least one Nash equilibrium with both players using pure strategies. The value of a strictly determined game is equal to the value of the equilibrium outcome. Most finite combinatorial games, like tic-tac-toe, chess, draughts, and go, are strictly determined games. Notes The study and classification of strictly determined games is distinct from the study of Determinacy, which is a subfield of set theory. See also * Solved game A solved game is a game whose outcome (win, lose or draw) can be correctly predicted from any position, assuming that both players play perfectly. This concept is usually applied to abstract strategy games, and especially to games with full informa ... References Game theory game classes {{Mathapplied-stub ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mathematics
Mathematics is an area of knowledge that includes the topics of numbers, formulas and related structures, shapes and the spaces in which they are contained, and quantities and their changes. These topics are represented in modern mathematics with the major subdisciplines of number theory, algebra, geometry, and analysis, respectively. There is no general consensus among mathematicians about a common definition for their academic discipline. Most mathematical activity involves the discovery of properties of abstract objects and the use of pure reason to prove them. These objects consist of either abstractions from nature orin modern mathematicsentities that are stipulated to have certain properties, called axioms. A ''proof'' consists of a succession of applications of deductive rules to already established results. These results include previously proved theorems, axioms, andin case of abstraction from naturesome basic properties that are considered true starting poin ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |