|
Giuseppe Carleo
Giuseppe Carleo (born 1984) is an Italian physicist. He is a professor of computational physics at EPFL (École Polytechnique Fédérale de Lausanne) and the head of the Laboratory of Computational Quantum Science. Career Carleo studied physics at the Sapienza University of Rome and in 2011 earned his PhD in theoretical physics at the International School for Advanced Studies under the supervision of Stefano Baroni. His thesis on "Spectral and dynamical properties of strongly correlated systems" was dedicated to novel numerical simulation techniques to study condensed-matter systems, such as the time-dependent variational Monte Carlo. As a Marie Curie Fellow he joined the École supérieure d'optique to work in the Lab directed by Alain Aspect on theoretically model and simulate ultra-cold atoms systems. In 2015, he went to work with the group of Matthias Troyer at the ETH Zurich where he later became a lecturer of computational quantum physics. Here he investigated the idea ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Italians
, flag = , flag_caption = The national flag of Italy , population = , regions = Italy 55,551,000 , region1 = Brazil , pop1 = 25–33 million , ref1 = , region2 = Argentina , pop2 = 20–25 million , ref2 = , region3 = United States , pop3 = 17-20 million , ref3 = , region4 = France , pop4 = 1-5 million , ref4 = , region5 = Venezuela , pop5 = 1-5 million , ref5 = , region6 = Paraguay , pop6 = 2.5 million , region7 = Colombia , pop7 = 2 million , ref7 = , region8 = Canada , pop8 = 1.5 million , ref8 = , region9 = Australia , pop9 = 1.0 million , ref9 = , region10 = Uruguay , pop10 = 1.0 million , r ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Ultra-cold Atoms
Ultracold atoms are atoms that are maintained at temperatures close to 0 kelvin (absolute zero), typically below several tens of microkelvin (µK). At these temperatures the atom's quantum-mechanical properties become important. To reach such low temperatures, a combination of several techniques typically has to be used. First, atoms are usually trapped and pre-cooled via laser cooling in a magneto-optical trap. To reach the lowest possible temperature, further cooling is performed using evaporative cooling in a magnetic or optical trap. Several Nobel prizes in physics are related to the development of the techniques to manipulate quantum properties of individual atoms (e.g. 1995-1997, 2001, 2005, 2012, 2017). Experiments with ultracold atoms study a variety of phenomena, including quantum phase transitions, Bose–Einstein condensation (BEC), bosonic superfluidity, quantum magnetism, many-body spin dynamics, Efimov states, Bardeen–Cooper–Schrieffer (BCS) superfluidity and t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Quantum Physics
Quantum mechanics is a fundamental theory in physics that provides a description of the physical properties of nature at the scale of atoms and subatomic particles. It is the foundation of all quantum physics including quantum chemistry, quantum field theory, quantum technology, and quantum information science. Classical physics, the collection of theories that existed before the advent of quantum mechanics, describes many aspects of nature at an ordinary (macroscopic) scale, but is not sufficient for describing them at small (atomic and subatomic) scales. Most theories in classical physics can be derived from quantum mechanics as an approximation valid at large (macroscopic) scale. Quantum mechanics differs from classical physics in that energy, momentum, angular momentum, and other quantities of a bound system are restricted to discrete values ( quantization); objects have characteristics of both particles and waves (wave–particle duality); and there are limits to ho ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
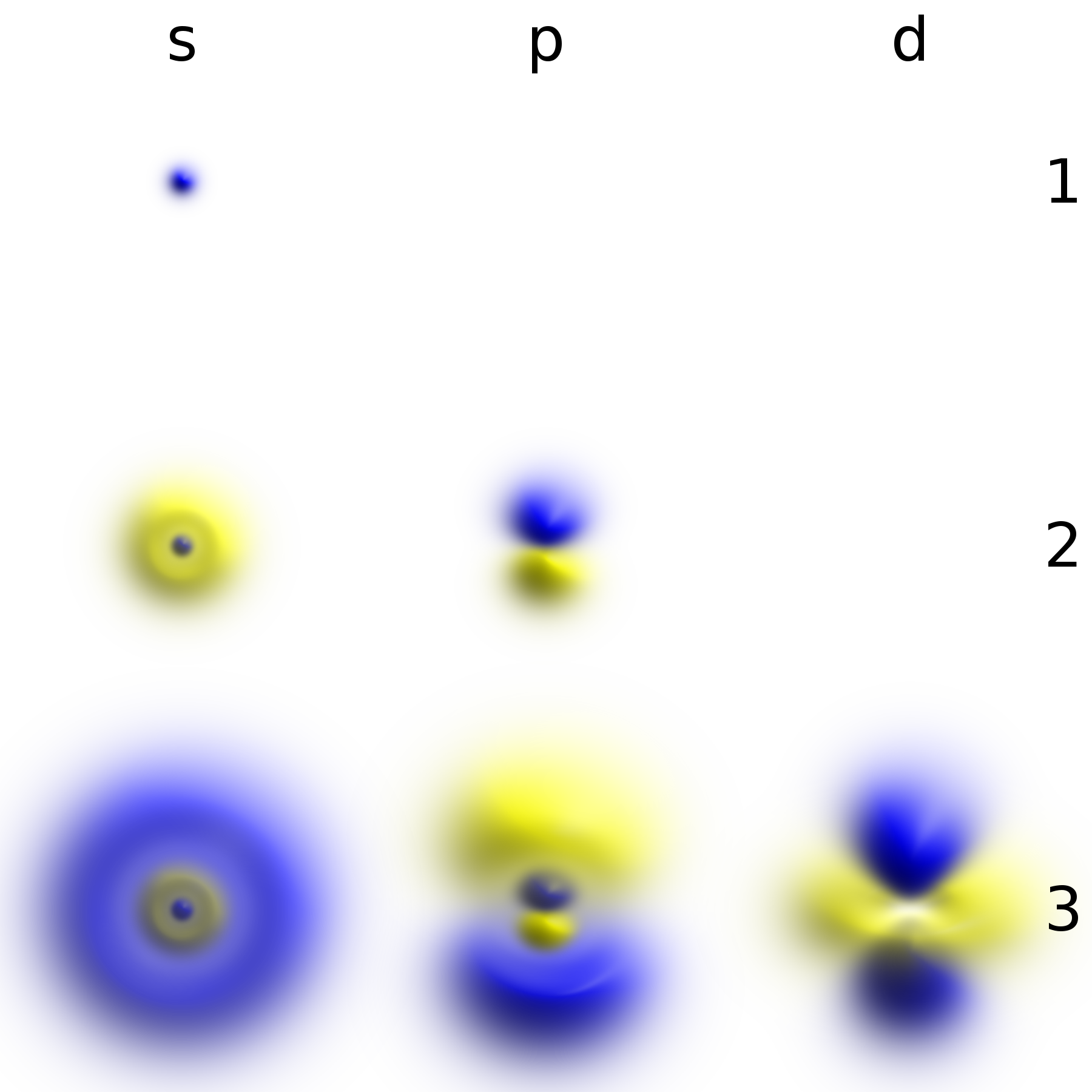
Wave Functions
A wave function in quantum physics is a mathematical description of the quantum state of an isolated quantum system. The wave function is a complex-valued probability amplitude, and the probabilities for the possible results of measurements made on the system can be derived from it. The most common symbols for a wave function are the Greek letters and (lower-case and capital psi, respectively). The wave function is a function of the degrees of freedom corresponding to some maximal set of commuting observables. Once such a representation is chosen, the wave function can be derived from the quantum state. For a given system, the choice of which commuting degrees of freedom to use is not unique, and correspondingly the domain of the wave function is also not unique. For instance, it may be taken to be a function of all the position coordinates of the particles over position space, or the momenta of all the particles over momentum space; the two are related by a Fourier transf ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Quantum Computing
Quantum computing is a type of computation whose operations can harness the phenomena of quantum mechanics, such as superposition, interference, and entanglement. Devices that perform quantum computations are known as quantum computers. Though current quantum computers may be too small to outperform usual (classical) computers for practical applications, larger realizations are believed to be capable of solving certain computational problems, such as integer factorization (which underlies RSA encryption), substantially faster than classical computers. The study of quantum computing is a subfield of quantum information science. There are several models of quantum computation with the most widely used being quantum circuits. Other models include the quantum Turing machine, quantum annealing, and adiabatic quantum computation. Most models are based on the quantum bit, or "qubit", which is somewhat analogous to the bit in classical computation. A qubit can be in a 1 or 0 quantum s ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Quantum Systems
Quantum mechanics is a fundamental theory in physics that provides a description of the physical properties of nature at the scale of atoms and subatomic particles. It is the foundation of all quantum physics including quantum chemistry, quantum field theory, quantum technology, and quantum information science. Classical physics, the collection of theories that existed before the advent of quantum mechanics, describes many aspects of nature at an ordinary (macroscopic) scale, but is not sufficient for describing them at small (atomic and subatomic) scales. Most theories in classical physics can be derived from quantum mechanics as an approximation valid at large (macroscopic) scale. Quantum mechanics differs from classical physics in that energy, momentum, angular momentum, and other quantities of a bound system are restricted to discrete values ( quantization); objects have characteristics of both particles and waves (wave–particle duality); and there are limits to how a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Computational Science
Computational science, also known as scientific computing or scientific computation (SC), is a field in mathematics that uses advanced computing capabilities to understand and solve complex problems. It is an area of science that spans many disciplines, but at its core, it involves the development of models and simulations to understand natural systems. * Algorithms ( numerical and non-numerical): mathematical models, computational models, and computer simulations developed to solve science (e.g., biological, physical, and social), engineering, and humanities problems * Computer hardware that develops and optimizes the advanced system hardware, firmware, networking, and data management components needed to solve computationally demanding problems * The computing infrastructure that supports both the science and engineering problem solving and the developmental computer and information science In practical use, it is typically the application of computer simulation and other fo ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
New York City
New York, often called New York City or NYC, is the List of United States cities by population, most populous city in the United States. With a 2020 population of 8,804,190 distributed over , New York City is also the List of United States cities by population density, most densely populated major city in the United States, and is more than twice as populous as second-place Los Angeles. New York City lies at the southern tip of New York (state), New York State, and constitutes the geographical and demographic center of both the Northeast megalopolis and the New York metropolitan area, the largest metropolitan area in the world by urban area, urban landmass. With over 20.1 million people in its metropolitan statistical area and 23.5 million in its combined statistical area as of 2020, New York is one of the world's most populous Megacity, megacities, and over 58 million people live within of the city. New York City is a global city, global Culture of New ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Simons Foundation
The Simons Foundation is a private foundation established in 1994 by Marilyn and Jim Simons with offices in New York City. As one of the largest charitable organizations in the US with assets of over $5 billion in 2022, the foundation's mission is to advance the frontiers of research in mathematics and the basic sciences. The foundation supports science by making grants to individual researchers and their projects. In 2021, Marilyn Simons stepped down as president after 26 years at the helm, and astrophysicist David Spergel was appointed president. The Flatiron Institute In 2016, the foundation launched the Flatiron Institute, its in-house multidisciplinary research institute focused on computational science. The Flatiron Institute hosts centers for computational science in five areas: Funding Areas The foundation makes grants in four program areas: Simons Investigators awardees Among other programs, the Simons Foundation funds the Simons Investigators in MPS program ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Flatiron Institute
The Flatiron Institute is an internal research division of the Simons Foundation, launched in 2016. It comprises five centers for computational science: the Center for Computational Astrophysics (CCA); the Center for Computational Biology (CCB); the Center for Computational Quantum Physics (CCQ); the Center for Computational Mathematics (CCM); and the Center for Computational Neuroscience (CCN). It also has a group called the Scientific Computing Core (SCC). The institute takes its name from the Flatiron District in New York City where it's based. The mission of the Flatiron Institute is to advance scientific research through computational methods, including data analysis, theory, modeling, and simulation. The Flatiron Institute was dedicated with a ceremony on September 6, 2017. Center for Computational Biology * Launched in 2013 as the Simons Center for Data Analysis * Director: Michael Shelley * Mission: CCB's mission is to develop modeling tools and theory for understanding ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Neural Network Quantum States
Neural Network Quantum States (NQS or NNQS) is a general class of variational quantum states parameterized in terms of an artificial neural network. It was first introduced in 2017 by the physicists Giuseppe Carleo and Matthias Troyer to approximate wave functions of many-body quantum systems. Given a many-body quantum state , \Psi\rangle comprising N degrees of freedom and a choice of associated quantum numbers s_1 \ldots s_N , then an NQS parameterizes the wave-function amplitudes \langle s_1 \ldots s_N , \Psi; W \rangle = F(s_1 \ldots s_N; W), where F(s_1 \ldots s_N; W) is an artificial neural network of parameters (weights) W , N input variables ( s_1 \ldots s_N ) and one complex-valued output corresponding to the wave-function amplitude. This variational form is used in conjunction with specific stochastic learning approaches to approximate quantum states of interest. Learning the Ground-State Wave Function One common application of NQS is to find an approxi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Variational Bayesian Methods
Variational Bayesian methods are a family of techniques for approximating intractable integrals arising in Bayesian inference and machine learning. They are typically used in complex statistical models consisting of observed variables (usually termed "data") as well as unknown parameters and latent variables, with various sorts of relationships among the three types of random variables, as might be described by a graphical model. As typical in Bayesian inference, the parameters and latent variables are grouped together as "unobserved variables". Variational Bayesian methods are primarily used for two purposes: #To provide an analytical approximation to the posterior probability of the unobserved variables, in order to do statistical inference over these variables. #To derive a lower bound for the marginal likelihood (sometimes called the ''evidence'') of the observed data (i.e. the marginal probability of the data given the model, with marginalization performed over unobserved v ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
.jpg "Click for more on -> Quantum Computing")
