|
Gauss–Lucas Theorem
In complex analysis, a branch of mathematics, the Gauss–Lucas theorem gives a geometric relation between the roots of a polynomial ''P'' and the roots of its derivative ''P′''. The set of roots of a real or complex polynomial is a set of points in the complex plane. The theorem states that the roots of ''P′'' all lie within the convex hull of the roots of ''P'', that is the smallest convex polygon containing the roots of ''P''. When ''P'' has a single root then this convex hull is a single point and when the roots lie on a line then the convex hull is a segment of this line. The Gauss–Lucas theorem, named after Carl Friedrich Gauss and Félix Lucas, is similar in spirit to Rolle's theorem. Formal statement If ''P'' is a (nonconstant) polynomial with complex coefficients, all zeros of ''P′'' belong to the convex hull of the set of zeros of ''P''. Special cases It is easy to see that if ''P''(''x'') = ''ax''2 + ''bx'' + ''c'' is a second degree polynomial, the ze ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Complex Analysis
Complex analysis, traditionally known as the theory of functions of a complex variable, is the branch of mathematical analysis that investigates Function (mathematics), functions of complex numbers. It is helpful in many branches of mathematics, including algebraic geometry, number theory, analytic combinatorics, applied mathematics; as well as in physics, including the branches of hydrodynamics, thermodynamics, and particularly quantum mechanics. By extension, use of complex analysis also has applications in engineering fields such as nuclear engineering, nuclear, aerospace engineering, aerospace, mechanical engineering, mechanical and electrical engineering. As a differentiable function of a complex variable is equal to its Taylor series (that is, it is Analyticity of holomorphic functions, analytic), complex analysis is particularly concerned with analytic functions of a complex variable (that is, holomorphic functions). History Complex analysis is one of the classical ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Marden's Theorem
In mathematics, Marden's theorem, named after Morris Marden but proved about 100 years earlier by Jörg Siebeck, gives a geometric relationship between the zeroes of a third-degree polynomial with complex coefficients and the zeroes of its derivative. See also geometrical properties of polynomial roots. Statement A cubic polynomial has three zeroes in the complex number plane, which in general form a triangle, and the Gauss–Lucas theorem states that the roots of its derivative lie within this triangle. Marden's theorem states their location within this triangle more precisely: :Suppose the zeroes , , and of a third-degree polynomial are non-collinear. There is a unique ellipse inscribed in the triangle with vertices , , and tangent to the sides at their midpoints: the Steiner inellipse. The foci of that ellipse are the zeroes of the derivative . Additional relations between root locations and the Steiner inellipse By the Gauss–Lucas theorem, the root of the double ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Descartes' Rule Of Signs
In mathematics, Descartes' rule of signs, first described by René Descartes in his work ''La Géométrie'', is a technique for getting information on the number of positive real roots of a polynomial. It asserts that the number of positive roots is at most the number of sign changes in the sequence of polynomial's coefficients (omitting the zero coefficients), and that the difference between these two numbers is always even. This implies, in particular, that if the number of sign changes is zero or one, then there are exactly zero or one positive roots, respectively. By a homographic transformation of the variable, one may use Descartes' rule of signs for getting a similar information on the number of roots in any interval. This is the basic idea of Budan's theorem and Budan–Fourier theorem. By repeating the division of an interval into two intervals, one gets eventually a list of disjoint intervals containing together all real roots of the polynomial, and containing each exact ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Hurwitz's Theorem (complex Analysis)
In mathematics and in particular the field of complex analysis, Hurwitz's theorem is a theorem associating the zeroes of a sequence of holomorphic, compact locally uniformly convergent functions with that of their corresponding limit. The theorem is named after Adolf Hurwitz. Statement Let be a sequence of holomorphic functions on a connected open set ''G'' that converge uniformly on compact subsets of ''G'' to a holomorphic function ''f'' which is not constantly zero on ''G''. If ''f'' has a zero of order ''m'' at ''z''0 then for every small enough ''ρ'' > 0 and for sufficiently large ''k'' ∈ N (depending on ''ρ''), ''fk'' has precisely ''m'' zeroes in the disk defined by , ''z'' − ''z''0, 0 such that ''f''(''z'') ≠ 0 in 0 ''δ'' for ''z'' on the circle , ''z'' − ''z''0, = ''ρ''. Since ''fk''(''z'') converges uniformly on the disc we have chosen, we can find ''N'' such that ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Routh–Hurwitz Theorem
In mathematics, the Routh–Hurwitz theorem gives a test to determine whether all root of a function, roots of a given polynomial lie in the left half-plane. Polynomials with this property are called stable polynomial, Hurwitz stable polynomials. The Routh-Hurwitz theorem is important in dynamical systems and control theory, because the characteristic polynomial of the differential equations of a linear stability, stable linear system has roots limited to the left half plane (negative eigenvalues). Thus the theorem provides a test to determine whether a linear dynamical system is stable without solving the system. Derivation of the Routh array, The Routh–Hurwitz theorem was proved in 1895, and it was named after Edward John Routh and Adolf Hurwitz. Notations Let ''f''(''z'') be a polynomial (with complex number, complex coefficients) of degree of a polynomial, degree ''n'' with no roots on the complex plane, imaginary axis (i.e. the line ''Z'' = ''ic'' where ''i'' is ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Sendov's Conjecture
In mathematics, Sendov's conjecture, sometimes also called Ilieff's conjecture, concerns the relationship between the locations of roots and critical points of a polynomial function of a complex variable. It is named after Blagovest Sendov. The conjecture states that for a polynomial : f(z) = (z - r_1)\cdots (z-r_n),\qquad (n\ge 2) with all roots ''r''1, ..., ''r''''n'' inside the closed unit disk , ''z'', ≤ 1, each of the ''n'' roots is at a distance no more than 1 from at least one critical point. The Gauss–Lucas theorem says that all of the critical points lie within the convex hull of the roots. It follows that the critical points must be within the unit disk, since the roots are. The conjecture has been proven for ''n'' < 9 by Brown-Xiang and for ''n'' sufficiently large by [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Bôcher's Theorem
In mathematics, Bôcher's theorem is either of two theorems named after the American mathematician Maxime Bôcher. Bôcher's theorem in complex analysis In complex analysis, the theorem states that the finite zeros of the derivative r'(z) of a non- constant rational function r(z) that are not multiple zeros are also the positions of equilibrium in the field of force due to particles of positive mass at the zeros of r(z) and particles of negative mass at the poles of r(z), with masses numerically equal to the respective multiplicities, where each particle repels with a force equal to the mass times the inverse distance. Furthermore, if ''C''1 and ''C''2 are two disjoint circular regions which contain respectively all the zeros and all the poles of r(z) , then ''C''1 and ''C''2 also contain all the critical points of r(z) . Bôcher's theorem for harmonic functions In the theory of harmonic functions, Bôcher's theorem states that a positive harmonic function in a punctured domai ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
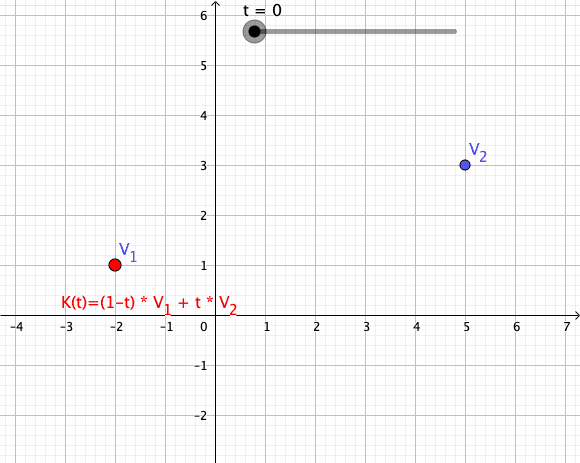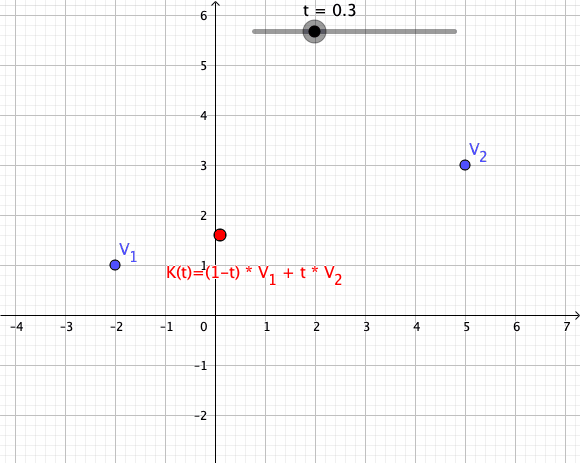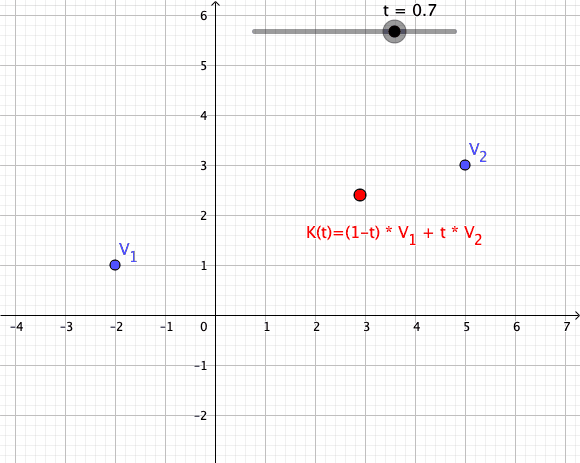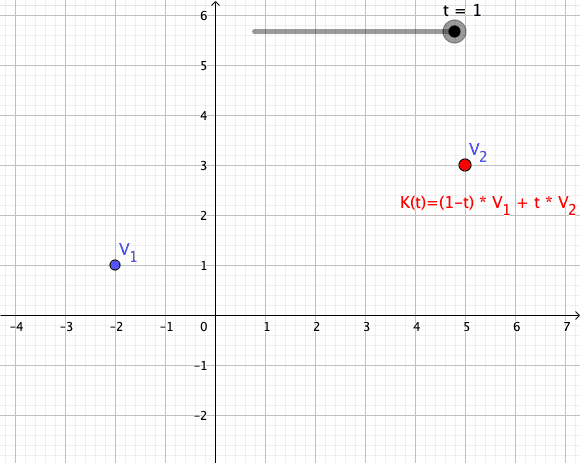
Convex Combination
In convex geometry and vector algebra, a convex combination is a linear combination of points (which can be vectors, scalars, or more generally points in an affine space) where all coefficients are non-negative and sum to 1. In other words, the operation is equivalent to a standard weighted average, but whose weights are expressed as a percent of the total weight, instead of as a fraction of the ''count'' of the weights as in a standard weighted average. More formally, given a finite number of points x_1, x_2, \dots, x_n in a real vector space, a convex combination of these points is a point of the form :\alpha_1x_1+\alpha_2x_2+\cdots+\alpha_nx_n where the real numbers \alpha_i satisfy \alpha_i\ge 0 and \alpha_1+\alpha_2+\cdots+\alpha_n=1. As a particular example, every convex combination of two points lies on the line segment between the points. A set is convex if it contains all convex combinations of its points. The convex hull of a given set of points is ident ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Barycentric Coordinates (astronomy)
In astronomy, the barycenter (or barycentre; ) is the center of mass of two or more bodies that orbit one another and is the point about which the bodies orbit. A barycenter is a dynamical point, not a physical object. It is an important concept in fields such as astronomy and astrophysics. The distance from a body's center of mass to the barycenter can be calculated as a two-body problem. If one of the two orbiting bodies is much more massive than the other and the bodies are relatively close to one another, the barycenter will typically be located within the more massive object. In this case, rather than the two bodies appearing to orbit a point between them, the less massive body will appear to orbit about the more massive body, while the more massive body might be observed to wobble slightly. This is the case for the Earth–Moon system, whose barycenter is located on average from Earth's center, which is 75% of Earth's radius of . When the two bodies are of similar mass ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Logarithmic Derivative
In mathematics, specifically in calculus and complex analysis, the logarithmic derivative of a function ''f'' is defined by the formula \frac where f' is the derivative of ''f''. Intuitively, this is the infinitesimal relative change in ''f''; that is, the infinitesimal absolute change in ''f,'' namely f', scaled by the current value of ''f.'' When ''f'' is a function ''f''(''x'') of a real variable ''x'', and takes real, strictly positive values, this is equal to the derivative of ln(''f''), or the natural logarithm of ''f''. This follows directly from the chain rule: \frac\ln f(x) = \frac \frac Basic properties Many properties of the real logarithm also apply to the logarithmic derivative, even when the function does ''not'' take values in the positive reals. For example, since the logarithm of a product is the sum of the logarithms of the factors, we have (\log uv)' = (\log u + \log v)' = (\log u)' + (\log v)' . So for positive-real-valued functions, the logarithmic d ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Real Number
In mathematics, a real number is a number that can be used to measure a ''continuous'' one-dimensional quantity such as a distance, duration or temperature. Here, ''continuous'' means that values can have arbitrarily small variations. Every real number can be almost uniquely represented by an infinite decimal expansion. The real numbers are fundamental in calculus (and more generally in all mathematics), in particular by their role in the classical definitions of limits, continuity and derivatives. The set of real numbers is denoted or \mathbb and is sometimes called "the reals". The adjective ''real'' in this context was introduced in the 17th century by René Descartes to distinguish real numbers, associated with physical reality, from imaginary numbers (such as the square roots of ), which seemed like a theoretical contrivance unrelated to physical reality. The real numbers include the rational numbers, such as the integer and the fraction . The rest of the real ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Preprint
In academic publishing, a preprint is a version of a scholarly or scientific paper that precedes formal peer review and publication in a peer-reviewed scholarly or scientific journal. The preprint may be available, often as a non-typeset version available free, before or after a paper is published in a journal. History Since 1991, preprints have increasingly been distributed electronically on the Internet, rather than as paper copies. This has given rise to massive preprint databases such as arXiv and HAL (open archive) etc. to institutional repositories. The sharing of preprints goes back to at least the 1960s, when the National Institutes of Health circulated biological preprints. After six years the use of these Information Exchange Groups was stopped, partially because journals stopped accepting submissions shared via these channels. In 2017, the Medical Research Council started supporting citations of preprints in grant and fellowship applications, and Wellcome Trust s ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |