|
GARCH
In econometrics, the autoregressive conditional heteroskedasticity (ARCH) model is a statistical model for time series data that describes the variance of the current error term or innovation as a function of the actual sizes of the previous time periods' error terms; often the variance is related to the squares of the previous innovations. The ARCH model is appropriate when the error variance in a time series follows an autoregressive (AR) model; if an autoregressive moving average (ARMA) model is assumed for the error variance, the model is a generalized autoregressive conditional heteroskedasticity (GARCH) model. ARCH models are commonly employed in modeling financial time series that exhibit time-varying volatility and volatility clustering, i.e. periods of swings interspersed with periods of relative calm (this is, when the time series exhibits heteroskedasticity). ARCH-type models are sometimes considered to be in the family of stochastic volatility models, although this ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Stochastic Volatility
In statistics, stochastic volatility models are those in which the variance of a stochastic process is itself randomly distributed. They are used in the field of mathematical finance to evaluate derivative securities, such as options. The name derives from the models' treatment of the underlying security's volatility as a random process, governed by state variables such as the price level of the underlying security, the tendency of volatility to revert to some long-run mean value, and the variance of the volatility process itself, among others. Stochastic volatility models are one approach to resolve a shortcoming of the Black–Scholes model. In particular, models based on Black-Scholes assume that the underlying volatility is constant over the life of the derivative, and unaffected by the changes in the price level of the underlying security. However, these models cannot explain long-observed features of the implied volatility surface such as volatility smile and skew, w ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Time Series
In mathematics, a time series is a series of data points indexed (or listed or graphed) in time order. Most commonly, a time series is a sequence taken at successive equally spaced points in time. Thus it is a sequence of discrete-time data. Examples of time series are heights of ocean tides, counts of sunspots, and the daily closing value of the Dow Jones Industrial Average. A time series is very frequently plotted via a run chart (which is a temporal line chart). Time series are used in statistics, signal processing, pattern recognition, econometrics, mathematical finance, weather forecasting, earthquake prediction, electroencephalography, control engineering, astronomy, communications engineering, and largely in any domain of applied science and engineering which involves temporal measurements. Time series ''analysis'' comprises methods for analyzing time series data in order to extract meaningful statistics and other characteristics of the data. Time series ''f ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
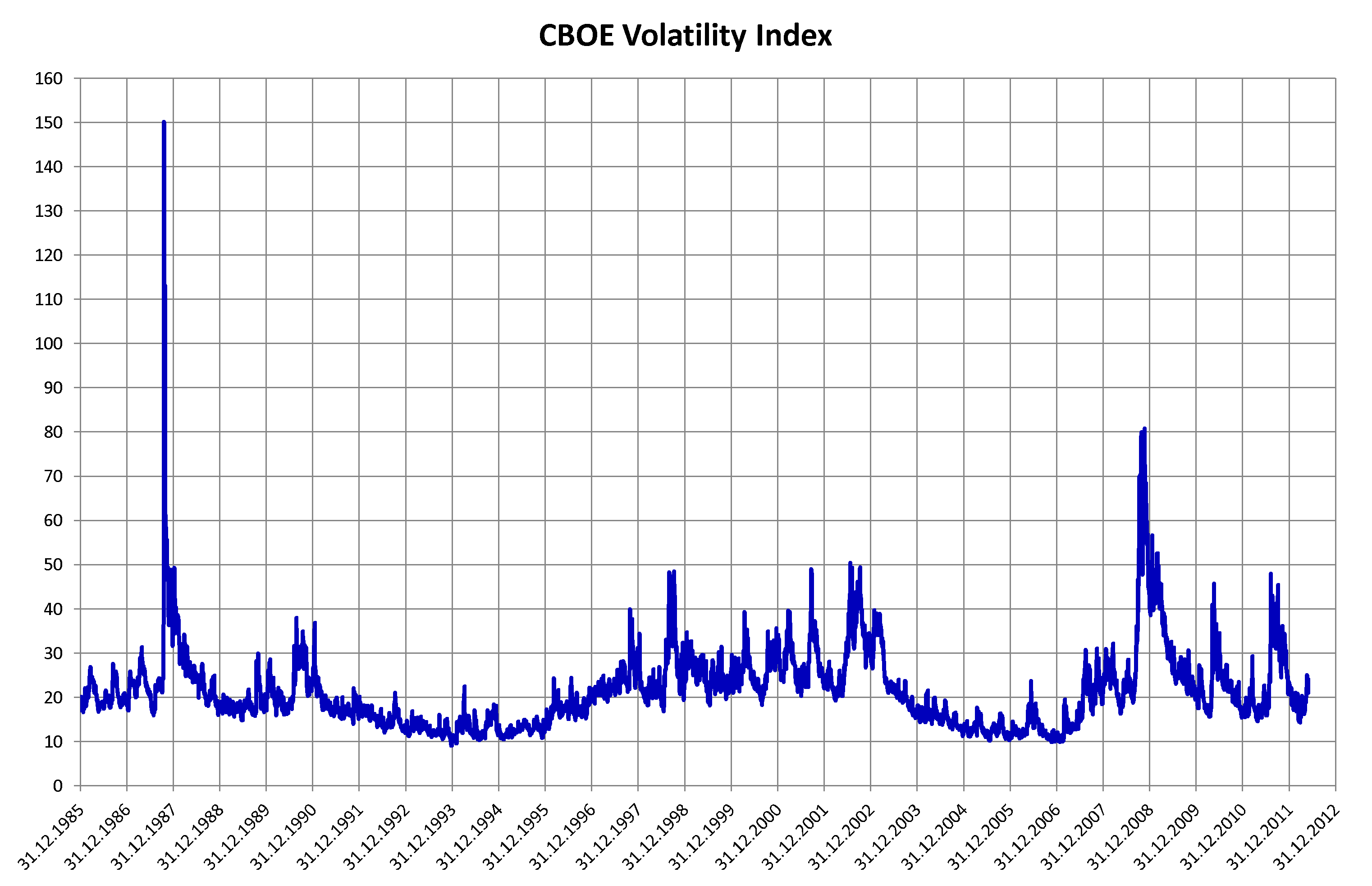
Volatility Clustering
In finance, volatility clustering refers to the observation, first noted by Mandelbrot (1963), that "large changes tend to be followed by large changes, of either sign, and small changes tend to be followed by small changes." A quantitative manifestation of this fact is that, while returns themselves are uncorrelated, absolute returns , r_, or their squares display a positive, significant and slowly decaying autocorrelation function: corr(, r, , , r , ) > 0 for τ ranging from a few minutes to several weeks. This empirical property has been documented in the 90's by Granger and Ding (1993) and Ding and Granger (1996) among others; see also. Some studies point further to long-range dependence in volatility time series, see Ding, Granger and Engle (1993) and Barndorff-Nielsen and Shephard. Observations of this type in financial time series go against simple random walk models and have led to the use of GARCH models and mean-reverting stochastic volatility models in financial fo ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Mathematical Finance
Mathematical finance, also known as quantitative finance and financial mathematics, is a field of applied mathematics, concerned with mathematical modeling in the financial field. In general, there exist two separate branches of finance that require advanced quantitative techniques: derivatives pricing on the one hand, and risk and portfolio management on the other. Mathematical finance overlaps heavily with the fields of computational finance and financial engineering. The latter focuses on applications and modeling, often with the help of stochastic asset models, while the former focuses, in addition to analysis, on building tools of implementation for the models. Also related is quantitative investing, which relies on statistical and numerical models (and lately machine learning) as opposed to traditional fundamental analysis when managing portfolios. French mathematician Louis Bachelier's doctoral thesis, defended in 1900, is considered the first scholarly work on ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Volatility (finance)
In finance, volatility (usually denoted by "sigma, σ") is the Variability (statistics), degree of variation of a trading price series over time, usually measured by the standard deviation of logarithmic returns. Historic volatility measures a time series of past market prices. Implied volatility looks forward in time, being derived from the market price of a market-traded derivative (in particular, an option). Volatility terminology Volatility as described here refers to the actual volatility, more specifically: * actual current volatility of a financial instrument for a specified period (for example 30 days or 90 days), based on historical prices over the specified period with the last observation the most recent price. * actual historical volatility which refers to the volatility of a financial instrument over a specified period but with the last observation on a date in the past **near synonymous is realized volatility, the square root of the realized variance, in turn c ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Econometrics
Econometrics is an application of statistical methods to economic data in order to give empirical content to economic relationships. M. Hashem Pesaran (1987). "Econometrics", '' The New Palgrave: A Dictionary of Economics'', v. 2, p. 8 p. 8–22 Reprinted in J. Eatwell ''et al.'', eds. (1990). ''Econometrics: The New Palgrave''p. 1 p. 1–34Abstract ( 2008 revision by J. Geweke, J. Horowitz, and H. P. Pesaran). More precisely, it is "the quantitative analysis of actual economic phenomena based on the concurrent development of theory and observation, related by appropriate methods of inference." An introductory economics textbook describes econometrics as allowing economists "to sift through mountains of data to extract simple relationships." Jan Tinbergen is one of the two founding fathers of econometrics. The other, Ragnar Frisch, also coined the term in the sense in which it is used today. A basic tool for econometrics is the multiple linear regression model. ''Econome ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
White Test
White test is a statistical test that establishes whether the variance of the errors in a regression model is constant: that is for homoskedasticity. This test, and an estimator for heteroscedasticity-consistent standard errors, were proposed by Halbert White in 1980. These methods have become widely used, making this paper one of the most cited articles in economics. In cases where the White test statistic is statistically significant, heteroskedasticity may not necessarily be the cause; instead the problem could be a specification error. In other words, the White test can be a test of heteroskedasticity or specification error or both. If no cross product terms are introduced in the White test procedure, then this is a test of pure heteroskedasticity. If cross products are introduced in the model, then it is a test of both heteroskedasticity and specification bias. Testing constant variance To test for constant variance one undertakes an auxiliary regression analysis: thi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Moving-average Model
In time series analysis, the moving-average model (MA model), also known as moving-average process, is a common approach for modeling univariate time series. The moving-average model specifies that the output variable is cross-correlated with a non-identical to itself random-variable. Together with the autoregressive (AR) model, the moving-average model is a special case and key component of the more general ARMA and ARIMA models of time series, which have a more complicated stochastic structure. Contrary to the AR model, the finite MA model is always stationary. The moving-average model should not be confused with the moving average, a distinct concept despite some similarities. Definition The notation MA(''q'') refers to the moving average model of order ''q'': : X_t = \mu + \varepsilon_t + \theta_1 \varepsilon_ + \cdots + \theta_q \varepsilon_ = \mu + \sum_^q \theta_i \varepsilon_ + \varepsilon_, where \mu is the mean of the series, the \theta_1,...,\theta_q are the co ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Ljung–Box Test
The Ljung–Box test (named for Greta M. Ljung and George E. P. Box) is a type of statistical test of whether any of a group of autocorrelations of a time series are different from zero. Instead of testing randomness at each distinct lag, it tests the "overall" randomness based on a number of lags, and is therefore a portmanteau test. This test is sometimes known as the Ljung–Box Q test, and it is closely connected to the Box–Pierce test (which is named after George E. P. Box and David A. Pierce). In fact, the Ljung–Box test statistic was described explicitly in the paper that led to the use of the Box–Pierce statistic, and from which that statistic takes its name. The Box–Pierce test statistic is a simplified version of the Ljung–Box statistic for which subsequent simulation studies have shown poor performance. The Ljung–Box test is widely applied in econometrics and other applications of time series analysis. A similar assessment can be also carried out with the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Null Hypothesis
The null hypothesis (often denoted ''H''0) is the claim in scientific research that the effect being studied does not exist. The null hypothesis can also be described as the hypothesis in which no relationship exists between two sets of data or variables being analyzed. If the null hypothesis is true, any experimentally observed effect is due to chance alone, hence the term "null". In contrast with the null hypothesis, an alternative hypothesis (often denoted ''H''A or ''H''1) is developed, which claims that a relationship does exist between two variables. Basic definitions The null hypothesis and the ''alternative hypothesis'' are types of conjectures used in statistical tests to make statistical inferences, which are formal methods of reaching conclusions and separating scientific claims from statistical noise. The statement being tested in a test of statistical significance is called the null hypothesis. The test of significance is designed to assess the strength of the e ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
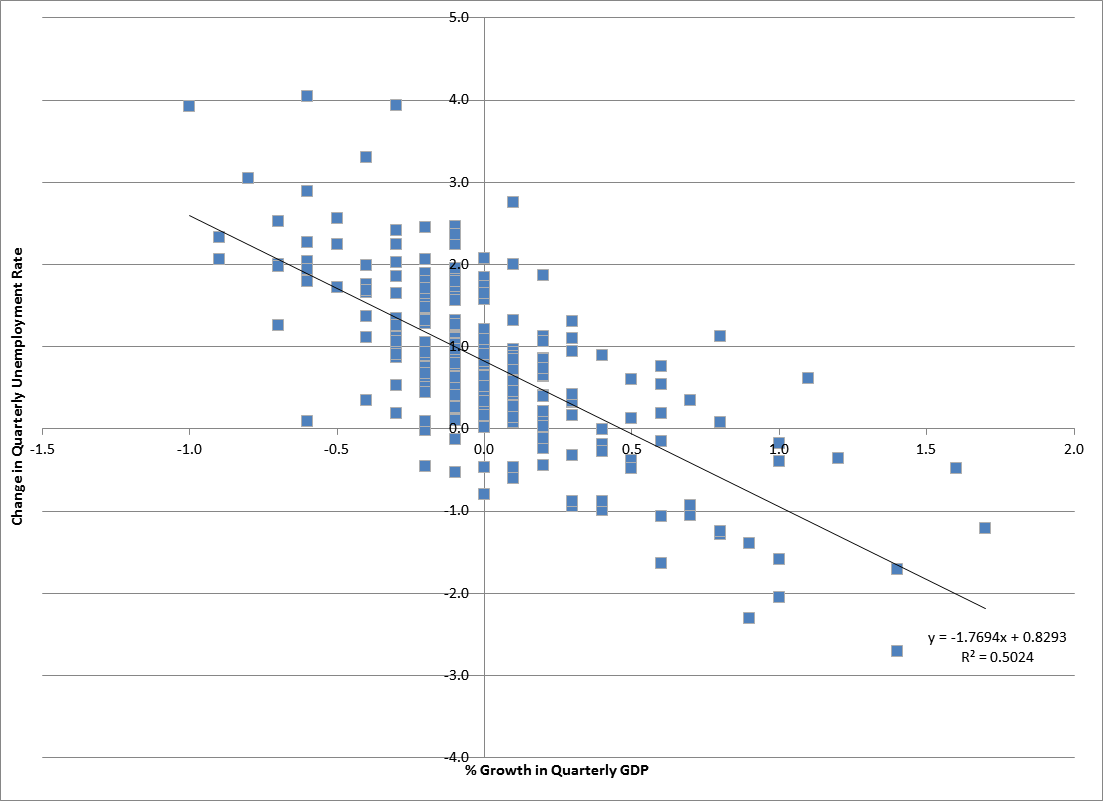
Conditional Variance
In probability theory and statistics, a conditional variance is the variance of a random variable given the value(s) of one or more other variables. Particularly in econometrics, the conditional variance is also known as the scedastic function or skedastic function. Conditional variances are important parts of autoregressive conditional heteroskedasticity (ARCH) models. Definition The conditional variance of a random variable ''Y'' given another random variable ''X'' is :\operatorname(Y\mid X) = \operatorname\Big(\big(Y - \operatorname(Y\mid X)\big)^\;\Big, \; X\Big). The conditional variance tells us how much variance is left if we use \operatorname(Y\mid X) to "predict" ''Y''. Here, as usual, \operatorname(Y\mid X) stands for the conditional expectation of ''Y'' given ''X'', which we may recall, is a random variable itself (a function of ''X'', determined up to probability one). As a result, \operatorname(Y\mid X) itself is a random variable (and is a function of ''X''). Expl ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |