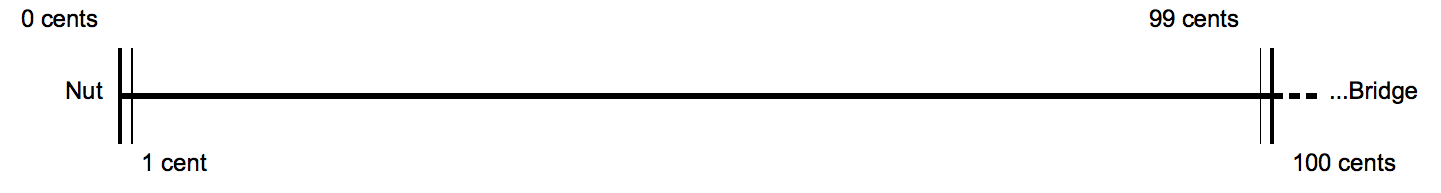|
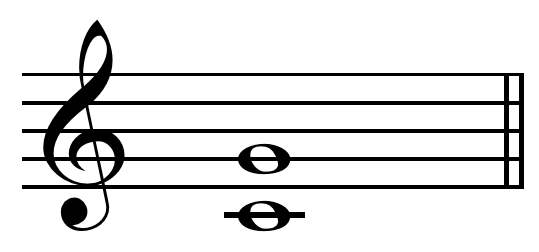
Guitar Harmonic
Playing a string harmonic (a flageolet) is a string instrument technique that uses the nodes of natural harmonics of a musical string to isolate overtones. Playing string harmonics produces high pitched tones, often compared in timbre to a whistle or flute. Overtones can be isolated "by lightly touching the string with the finger instead of pressing it down" against the fingerboard (without stopping). For some instruments this is a fundamental technique, such as the Chinese guqin, where it is known as ''fan yin'' ( 泛音, lit. "floating sound"), and the Vietnamese đàn bầu. Overtones When a string is plucked or bowed normally, the ear hears the fundamental frequency most prominently, but the overall sound is also colored by the presence of various overtones (frequencies greater than the fundamental frequency). The fundamental frequency and its overtones are perceived by the listener as a single note; however, different combinations of overtones give rise to noticeably differ ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Timbre
In music, timbre ( ), also known as tone color or tone quality (from psychoacoustics), is the perceived sound quality of a musical note, sound or musical tone, tone. Timbre distinguishes different types of sound production, such as choir voices and musical instruments. It also enables listeners to distinguish different instruments in the same category (e.g., an oboe and a clarinet, both Woodwind instrument, woodwind instruments). In simple terms, timbre is what makes a particular musical instrument or human voice have a different sound from another, even when they play or sing the same note. For instance, it is the difference in sound between a guitar and a piano playing the same note at the same volume. Both instruments can sound equally tuned in relation to each other as they play the same note, and while playing at the same amplitude level each instrument will still sound distinctively with its own unique tone color. Experienced musicians are able to distinguish between diff ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Whole Tone
In Western music theory, a major second (sometimes also called whole tone or a whole step) is a second spanning two semitones (). A second is a musical interval encompassing two adjacent staff positions (see Interval number for more details). For example, the interval from C to D is a major second, as the note D lies two semitones above C, and the two notes are notated on adjacent staff positions. Diminished, minor and augmented seconds are notated on adjacent staff positions as well, but consist of a different number of semitones (zero, one, and three). The major second is the interval that occurs between the first and second degrees of a major scale, the tonic and the supertonic. On a musical keyboard, a major second is the interval between two keys separated by one key, counting white and black keys alike. On a guitar string, it is the interval separated by two frets. In moveable-do solfège, it is the interval between ''do'' and ''re''. It is considered a melodi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Pythagorean Interval
In musical tuning theory, a Pythagorean interval is a musical interval with frequency ratio equal to a power of two divided by a power of three, or vice versa.Benson, Donald C. (2003). ''A Smoother Pebble: Mathematical Explorations'', p.56. . "The frequency ratio of every Pythagorean interval is a ratio between a power of two and a power of three...confirming the Pythagorean requirements that all intervals be associated with ratios of whole numbers." For instance, the perfect fifth with ratio 3/2 (equivalent to 31/ 21) and the perfect fourth with ratio 4/3 (equivalent to 22/ 31) are Pythagorean intervals. All the intervals between the notes of a scale are Pythagorean if they are tuned using the Pythagorean tuning system. However, some Pythagorean intervals are also used in other tuning systems. For instance, the above-mentioned Pythagorean perfect fifth and fourth are also used in just intonation. Interval table Notice that the terms ''ditone'' and ''semiditone'' are specific ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Septimal Major Second
In music, the septimal whole tone, septimal major second, or supermajor second is the musical interval exactly or approximately equal to an 8/7 ratio of frequencies.Andrew Horner, Lydia Ayres (2002). ''Cooking with Csound: Woodwind and Brass Recipes'', p.131. . "Super-Major Second". It is about 231 cents wide in just intonation.Leta E. Miller, Fredric Lieberman (2006). ''Lou Harrison'', p.72. . 24 equal temperament does not match this interval particularly well, its nearest representation being at 250 cents, approximately 19 cents sharp. The septimal whole tone may be derived from the harmonic series as the interval between the seventh and eighth harmonics and the term ''septimal'' refers to the fact that it utilizes the seventh harmonic. It can also be thought of as the octave inversion of the 7/4 interval, the harmonic seventh. No close approximation to this interval exists in the standard 12 equal temperament used in most modern western music. The very simple 5 equal ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Harmonic Seventh
The harmonic seventh interval, also known as the septimal minor seventh, or subminor seventh, is one with an exact 7:4 ratio (about 969 cents). This is somewhat narrower than and is, "particularly sweet", "sweeter in quality" than an "ordinary" just minor seventh, which has an intonation ratio of 9:5 (about 1018 cents). The harmonic seventh arises from the harmonic series as the interval between the fourth harmonic (second octave of the fundamental) and the seventh harmonic; in that octave, harmonics 4, 5, 6, and 7 constitute a purely consonant major chord with added seventh (root position). When played on the natural horn, as a compromise the note is often adjusted to 16:9 of the root (for C maj7, the substituted note is B, 996.09 cents), but some pieces call for the pure harmonic seventh, including Britten's ''Serenade for Tenor, Horn and Strings''. Composer Ben Johnston uses a small "7" as an accidental to indicate a note is lowered 49 cents ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Minor Third
In music theory, a minor third is a musical interval that encompasses three half steps, or semitones. Staff notation represents the minor third as encompassing three staff positions (see: interval number). The minor third is one of two commonly occurring thirds. It is called ''minor'' because it is the smaller of the two: the major third spans an additional semitone. For example, the interval from A to C is a minor third, as the note C lies three semitones above A. Coincidentally, there are three staff positions from A to C. Diminished and augmented thirds span the same number of staff positions, but consist of a different number of semitones (two and five). The minor third is a skip melodically. Notable examples of ascending minor thirds include the opening two notes of " Greensleeves" and of " Light My Fire". The minor third may be derived from the harmonic series as the interval between the fifth and sixth harmonics, or from the 19th harmonic. The minor third is co ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Just Major Third
Just or JUST may refer to: __NOTOC__ People * Just (surname) * Just (given name) Arts and entertainment * ''Just'', a 1998 album by Dave Lindholm * "Just" (song), a song by Radiohead * "Just", a song from the album ''Lost and Found'' by Mudvayne * ''Just!'' (series), a series of short-story collections for children by Andy Griffiths JUST * Jordan University of Science and Technology, Jordan * Jessore University of Science & Technology, Bangladesh * Jinwen University of Science and Technology, New Taipei, Taiwan Businesses * Just Group plc, a British company specialising in retirement products and services * Just Group, an Australian owner and operator of seven retail brands * JUST, Inc., an American food manufacturing company See also * * List of people known as the Just * Saint-Just (other) * Justice Justice, in its broadest sense, is the principle that people receive that which they deserve, with the interpretation of what then constitutes "deserving" bein ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Perfect Fourth
A fourth is a musical interval encompassing four staff positions in the music notation of Western culture, and a perfect fourth () is the fourth spanning five semitones (half steps, or half tones). For example, the ascending interval from C to the next F is a perfect fourth, because the note F is the fifth semitone above C, and there are four staff positions between C and F. Diminished and augmented fourths span the same number of staff positions, but consist of a different number of semitones (four and six, respectively). The perfect fourth may be derived from the harmonic series as the interval between the third and fourth harmonics. The term ''perfect'' identifies this interval as belonging to the group of perfect intervals, so called because they are neither major nor minor. A perfect fourth in just intonation corresponds to a pitch ratio of 4:3, or about 498 cents (), while in equal temperament a perfect fourth is equal to five semitones, or 500 cents (see additive s ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Perfect Fifth
In music theory, a perfect fifth is the Interval (music), musical interval corresponding to a pair of pitch (music), pitches with a frequency ratio of 3:2, or very nearly so. In classical music from Western culture, a fifth is the interval from the first to the last of five consecutive Musical note, notes in a diatonic scale. The perfect fifth (often abbreviated P5) spans seven semitones, while the Tritone, diminished fifth spans six and the augmented fifth spans eight semitones. For example, the interval from C to G is a perfect fifth, as the note G lies seven semitones above C. The perfect fifth may be derived from the Harmonic series (music), harmonic series as the interval between the second and third harmonics. In a diatonic scale, the dominant (music), dominant note is a perfect fifth above the tonic (music), tonic note. The perfect fifth is more consonance and dissonance, consonant, or stable, than any other interval except the unison and the octave. It occurs above the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Octave
In music, an octave ( la, octavus: eighth) or perfect octave (sometimes called the diapason) is the interval between one musical pitch and another with double its frequency. The octave relationship is a natural phenomenon that has been referred to as the "basic miracle of music," the use of which is "common in most musical systems." The interval between the first and second harmonics of the harmonic series is an octave. In Western music notation, notes separated by an octave (or multiple octaves) have the same name and are of the same pitch class. To emphasize that it is one of the perfect intervals (including unison, perfect fourth, and perfect fifth), the octave is designated P8. Other interval qualities are also possible, though rare. The octave above or below an indicated note is sometimes abbreviated ''8a'' or ''8va'' ( it, all'ottava), ''8va bassa'' ( it, all'ottava bassa, sometimes also ''8vb''), or simply ''8'' for the octave in the direction indicated by placing ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Cent (music)
The cent is a logarithmic unit of measure used for musical intervals. Twelve-tone equal temperament divides the octave into 12 semitones of 100 cents each. Typically, cents are used to express small intervals, or to compare the sizes of comparable intervals in different tuning systems, and in fact the interval of one cent is too small to be perceived between successive notes. Cents, as described by Alexander John Ellis, follow a tradition of measuring intervals by logarithms that began with Juan Caramuel y Lobkowitz in the 17th century. Ellis chose to base his measures on the hundredth part of a semitone, , at Robert Holford Macdowell Bosanquet's suggestion. He made extensive measurements of musical instruments from around the world, using cents extensively to report and compare the scales employed, and further described and employed the system in his 1875 edition of Hermann von Helmholtz's ''On the Sensations of Tone''. It has become the standard method of representing ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |

.jpg)