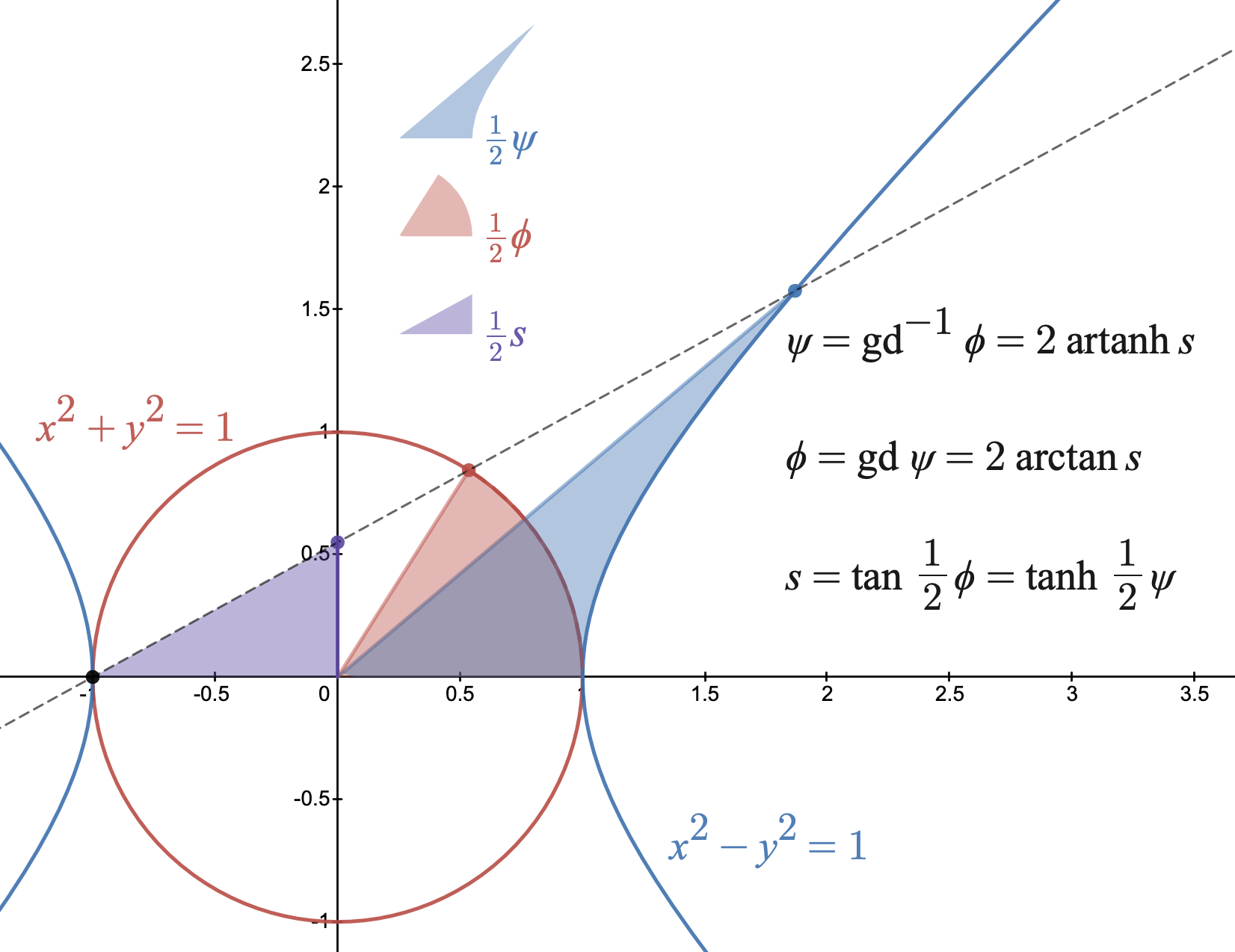
|
Gudermannian Conformal Map
In mathematics, the Gudermannian function relates a hyperbolic angle measure \psi to a circular angle measure \phi called the ''gudermannian'' of \psi and denoted \operatorname\psi. The Gudermannian function reveals a close relationship between the circular functions and hyperbolic functions. It was introduced in the 1760s by Johann Heinrich Lambert, and later named for Christoph Gudermann who also described the relationship between circular and hyperbolic functions in 1830. The gudermannian is sometimes called the hyperbolic amplitude as a limiting case of the Jacobi elliptic amplitude \operatorname(\psi, m) when parameter m=1. The real Gudermannian function is typically defined for -\infty < \psi < \infty to be the integral of the hyperbolic secant The real inverse Gudermannian function can be defined for as the [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Gudermannian Function
In mathematics, the Gudermannian function relates a hyperbolic angle measure \psi to a circular angle measure \phi called the ''gudermannian'' of \psi and denoted \operatorname\psi. The Gudermannian function reveals a close relationship between the circular functions and hyperbolic functions. It was introduced in the 1760s by Johann Heinrich Lambert, and later named for Christoph Gudermann who also described the relationship between circular and hyperbolic functions in 1830. The gudermannian is sometimes called the hyperbolic amplitude as a limiting case of the Jacobi elliptic amplitude \operatorname(\psi, m) when parameter m=1. The real Gudermannian function is typically defined for -\infty < \psi < \infty to be the integral of the hyperbolic secant The real inverse Gudermannian function can be defined for as the [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Integral Of The Secant Function
In calculus, the integral of the secant function can be evaluated using a variety of methods and there are multiple ways of expressing the antiderivative, all of which can be shown to be equivalent via trigonometric identities, : \int \sec \theta \, d\theta = \begin \dfrac12 \ln \left, \dfrac\ + C \\ 5pt\ln\left, \sec\theta + \tan\theta\ + C \\ 5pt\ln\left, \tan\left(\dfrac + \dfrac\right) \ + C\\ 5pt\end This formula is useful for evaluating various trigonometric integrals. In particular, it can be used to evaluate the integral of the secant cubed, which, though seemingly special, comes up rather frequently in applications. Proof that the different antiderivatives are equivalent Trigonometric forms : \int \sec \theta \, d\theta = \left\\text The second of these follows by first multiplying top and bottom of the interior fraction by . This gives in the denominator, and the result follows by moving the factor of into the logarithm as a square root. Leaving out the const ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Complex Analysis
Complex analysis, traditionally known as the theory of functions of a complex variable, is the branch of mathematical analysis that investigates Function (mathematics), functions of complex numbers. It is helpful in many branches of mathematics, including algebraic geometry, number theory, analytic combinatorics, applied mathematics; as well as in physics, including the branches of hydrodynamics, thermodynamics, and particularly quantum mechanics. By extension, use of complex analysis also has applications in engineering fields such as nuclear engineering, nuclear, aerospace engineering, aerospace, mechanical engineering, mechanical and electrical engineering. As a differentiable function of a complex variable is equal to its Taylor series (that is, it is Analyticity of holomorphic functions, analytic), complex analysis is particularly concerned with analytic functions of a complex variable (that is, holomorphic functions). History Complex analysis is one of the classical ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Gudermannian Conformal Map
In mathematics, the Gudermannian function relates a hyperbolic angle measure \psi to a circular angle measure \phi called the ''gudermannian'' of \psi and denoted \operatorname\psi. The Gudermannian function reveals a close relationship between the circular functions and hyperbolic functions. It was introduced in the 1760s by Johann Heinrich Lambert, and later named for Christoph Gudermann who also described the relationship between circular and hyperbolic functions in 1830. The gudermannian is sometimes called the hyperbolic amplitude as a limiting case of the Jacobi elliptic amplitude \operatorname(\psi, m) when parameter m=1. The real Gudermannian function is typically defined for -\infty < \psi < \infty to be the integral of the hyperbolic secant The real inverse Gudermannian function can be defined for as the [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Riemann Sphere
In mathematics, the Riemann sphere, named after Bernhard Riemann, is a model of the extended complex plane: the complex plane plus one point at infinity. This extended plane represents the extended complex numbers, that is, the complex numbers plus a value \infty for infinity. With the Riemann model, the point \infty is near to very large numbers, just as the point 0 is near to very small numbers. The extended complex numbers are useful in complex analysis because they allow for division by zero in some circumstances, in a way that makes expressions such as 1/0=\infty well-behaved. For example, any rational function on the complex plane can be extended to a holomorphic function on the Riemann sphere, with the poles of the rational function mapping to infinity. More generally, any meromorphic function can be thought of as a holomorphic function whose codomain is the Riemann sphere. In geometry, the Riemann sphere is the prototypical example of a Riemann surface, and is one of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Möbius Transformation
In geometry and complex analysis, a Möbius transformation of the complex plane is a rational function of the form f(z) = \frac of one complex variable ''z''; here the coefficients ''a'', ''b'', ''c'', ''d'' are complex numbers satisfying ''ad'' − ''bc'' ≠ 0. Geometrically, a Möbius transformation can be obtained by first performing stereographic projection from the plane to the unit two-sphere, rotating and moving the sphere to a new location and orientation in space, and then performing stereographic projection (from the new position of the sphere) to the plane. These transformations preserve angles, map every straight line to a line or circle, and map every circle to a line or circle. The Möbius transformations are the projective transformations of the complex projective line. They form a group called the Möbius group, which is the projective linear group PGL(2,C). Together with its subgroups, it has numerous applications in mathematics and physics. Möbius transfor ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Exponential Function
The exponential function is a mathematical function denoted by f(x)=\exp(x) or e^x (where the argument is written as an exponent). Unless otherwise specified, the term generally refers to the positive-valued function of a real variable, although it can be extended to the complex numbers or generalized to other mathematical objects like matrices or Lie algebras. The exponential function originated from the notion of exponentiation (repeated multiplication), but modern definitions (there are several equivalent characterizations) allow it to be rigorously extended to all real arguments, including irrational numbers. Its ubiquitous occurrence in pure and applied mathematics led mathematician Walter Rudin to opine that the exponential function is "the most important function in mathematics". The exponential function satisfies the exponentiation identity e^ = e^x e^y \text x,y\in\mathbb, which, along with the definition e = \exp(1), shows that e^n=\underbrace_ for positive i ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Branch Point
In the mathematical field of complex analysis, a branch point of a multi-valued function (usually referred to as a "multifunction" in the context of complex analysis) is a point such that if the function is n-valued (has n values) at that point, all of its neighborhoods contain a point that has more than n values. Multi-valued functions are rigorously studied using Riemann surfaces, and the formal definition of branch points employs this concept. Branch points fall into three broad categories: algebraic branch points, transcendental branch points, and logarithmic branch points. Algebraic branch points most commonly arise from functions in which there is an ambiguity in the extraction of a root, such as solving the equation ''w''2 = ''z'' for ''w'' as a function of ''z''. Here the branch point is the origin, because the analytic continuation of any solution around a closed loop containing the origin will result in a different function: there is non-trivial monodromy. ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Gudermannian Identities
In mathematics, the Gudermannian function relates a hyperbolic angle measure \psi to a circular angle measure \phi called the ''gudermannian'' of \psi and denoted \operatorname\psi. The Gudermannian function reveals a close relationship between the circular functions and hyperbolic functions. It was introduced in the 1760s by Johann Heinrich Lambert, and later named for Christoph Gudermann who also described the relationship between circular and hyperbolic functions in 1830. The gudermannian is sometimes called the hyperbolic amplitude as a limiting case of the Jacobi elliptic amplitude \operatorname(\psi, m) when parameter m=1. The real Gudermannian function is typically defined for -\infty < \psi < \infty to be the integral of the hyperbolic secant The real inverse Gudermannian function can be defined for as the [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Integration By Substitution
In calculus, integration by substitution, also known as ''u''-substitution, reverse chain rule or change of variables, is a method for evaluating integrals and antiderivatives. It is the counterpart to the chain rule for differentiation, and can loosely be thought of as using the chain rule "backwards". Substitution for a single variable Introduction Before stating the result rigorously, consider a simple case using indefinite integrals. Compute \textstyle\int(2x^3+1)^7(x^2)\,dx. Set u=2x^3+1. This means \textstyle\frac=6x^2, or in differential form, du=6x^2\,dx. Now :\int(2x^3 +1)^7(x^2)\,dx = \frac\int\underbrace_\underbrace_=\frac\int u^\,du=\frac\left(\fracu^\right)+C=\frac(2x^3+1)^+C, where C is an arbitrary constant of integration. This procedure is frequently used, but not all integrals are of a form that permits its use. In any event, the result should be verified by differentiating and comparing to the original integrand. :\frac\left frac(2x^3+1)^+C\right\f ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Weierstrass Substitution
In integral calculus, the tangent half-angle substitution is a change of variables used for evaluating integrals, which converts a rational function of trigonometric functions of x into an ordinary rational function of t by setting t = \tan \tfrac x2. This is the one-dimensional stereographic projection of the unit circle parametrized by angle measure onto the real line. The general transformation formula is: \int f(\sin x, \cos x)\, dx =\int f \frac. The tangent of half an angle is important in spherical trigonometry and was sometimes known in the 17th century as the half tangent or semi-tangent. Leonhard Euler used it to evaluate the integral \int dx / (a + b\cos x) in his 1768 integral calculus textbook, and Adrien-Marie Legendre described the general method in 1817. The substitution is described in most integral calculus textbooks since the late 19th century, usually without any special name. It is known in Russia as the universal trigonometric substitution, and also known ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Complex Plane
In mathematics, the complex plane is the plane formed by the complex numbers, with a Cartesian coordinate system such that the -axis, called the real axis, is formed by the real numbers, and the -axis, called the imaginary axis, is formed by the imaginary numbers. The complex plane allows a geometric interpretation of complex numbers. Under addition, they add like vectors. The multiplication of two complex numbers can be expressed more easily in polar coordinates—the magnitude or ''modulus'' of the product is the product of the two absolute values, or moduli, and the angle or ''argument'' of the product is the sum of the two angles, or arguments. In particular, multiplication by a complex number of modulus 1 acts as a rotation. The complex plane is sometimes known as the Argand plane or Gauss plane. Notational conventions Complex numbers In complex analysis, the complex numbers are customarily represented by the symbol ''z'', which can be separated into its real (''x'') and ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
