|
Greeks (finance)
In mathematical finance, the Greeks are the quantities representing the sensitivity of the price of derivatives such as options to a change in underlying parameters on which the value of an instrument or portfolio of financial instruments is dependent. The name is used because the most common of these sensitivities are denoted by Greek letters (as are some other finance measures). Collectively these have also been called the risk sensitivities, risk measures or hedge parameters. Use of the Greeks The Greeks are vital tools in risk management. Each Greek measures the sensitivity of the value of a portfolio to a small change in a given underlying parameter, so that component risks may be treated in isolation, and the portfolio rebalanced accordingly to achieve a desired exposure; see for example delta hedging. The Greeks in the Black–Scholes model are relatively easy to calculate, a desirable property of financial models, and are very useful for derivatives traders, especi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Veta
''Veta'' () is a 1986 Indian Telugu-language period action film starring Chiranjeevi, Jaya Prada and Sumalatha. It was released on 28 May 1986. The film was made by Samyuktha Movies, whose earlier blockbuster was '' Khaidi''. The movie is based on Alexandre Dumas' 1844 novel ''The Count of Monte Cristo''. The successful team of director A. Kodandarami Reddy, composer K. Chakravarthy and writers Paruchuri brothers was repeated in this movie as well. Plot Set in 1939, Pratap (Chiranjeevi) is a sailor working on a ship during the British rule of India. He is in love with a wealthy woman, played by Jaya Prada. Jaya Prada's cousin (బావ) Jayaram, who works for the British army, also wants to marry her. When the captain of the ship (C. S. Rao) is poisoned and killed by two of the crew members, Jayaram uses his power to twist Benarjee (Ranganath) and deports Pratap away for good at the secluded Andaman Jail. Pratap is trapped in this nightmare that lasts for thirteen years. Th ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Speed
In everyday use and in kinematics, the speed (commonly referred to as ''v'') of an object is the magnitude of the change of its position over time or the magnitude of the change of its position per unit of time; it is thus a scalar quantity. The average speed of an object in an interval of time is the distance travelled by the object divided by the duration of the interval; the instantaneous speed is the limit of the average speed as the duration of the time interval approaches zero. Speed is not the same as velocity. Speed has the dimensions of distance divided by time. The SI unit of speed is the metre per second (m/s), but the most common unit of speed in everyday usage is the kilometre per hour (km/h) or, in the US and the UK, miles per hour (mph). For air and marine travel, the knot is commonly used. The fastest possible speed at which energy or information can travel, according to special relativity, is the speed of light in a vacuum ''c'' = metres per seco ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Beta (finance)
In finance, the beta (β or market beta or beta coefficient) is a measure of how an individual asset moves (on average) when the overall stock market increases or decreases. Thus, beta is a useful measure of the contribution of an individual asset to the risk of the market portfolio when it is added in small quantity. Thus, beta is referred to as an asset's non-diversifiable risk, its systematic risk, market risk, or hedge ratio. Beta is ''not'' a measure of idiosyncratic risk. Interpretation of values By definition, the value-weighted average of all market-betas of all investable assets with respect to the value-weighted market index is 1. If an asset has a beta above (below) 1, it indicates that its return moves more (less) than 1-to-1 with the return of the market-portfolio, on average. In practice, few stocks have negative betas (tending to go up when the market goes down). Most stocks have betas between 0 and 3. Treasury bills (like most fixed income instrumen ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Alpha (finance)
Alpha is a measure of the active return on an investment, the performance of that investment compared with a suitable market index. An alpha of 1% means the investment's return on investment over a selected period of time was 1% better than the market during that same period; a negative alpha means the investment underperformed the market. Alpha, along with beta, is one of two key coefficients in the capital asset pricing model used in modern portfolio theory and is closely related to other important quantities such as standard deviation, R-squared and the Sharpe ratio. In modern financial markets, where index funds are widely available for purchase, alpha is commonly used to judge the performance of mutual funds and similar investments. As these funds include various fees normally expressed in percent terms, the fund has to maintain an alpha greater than its fees in order to provide positive gains compared with an index fund. Historically, the vast majority of traditional fu ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Risk-free Interest Rate
The risk-free rate of return, usually shortened to the risk-free rate, is the rate of return of a hypothetical investment with scheduled payments over a fixed period of time that is assumed to meet all payment obligations. Since the risk-free rate can be obtained with no risk, any other investment having some risk will have to have a higher rate of return in order to induce any investors to hold it. In practice, to infer the risk-free interest rate in a particular currency, market participants often choose the yield to maturity on a risk-free bond issued by a government of the same currency whose risks of default are so low as to be negligible. For example, the rate of return on T-bills is sometimes seen as the risk-free rate of return in US dollars. Theoretical measurement As stated by Malcolm Kemp in chapter five of his book ''Market Consistency: Model Calibration in Imperfect Markets'', the risk-free rate means different things to different people and there is no consensus ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Model (economics)
In economics, a model is a theoretical construct representing economic processes by a set of variables and a set of logical and/or quantitative relationships between them. The economic model is a simplified, often mathematical, framework designed to illustrate complex processes. Frequently, economic models posit structural parameters. A model may have various exogenous variables, and those variables may change to create various responses by economic variables. Methodological uses of models include investigation, theorizing, and fitting theories to the world. Overview In general terms, economic models have two functions: first as a simplification of and abstraction from observed data, and second as a means of selection of data based on a paradigm of econometric study. ''Simplification'' is particularly important for economics given the enormous complexity of economic processes. This complexity can be attributed to the diversity of factors that determine economic activit ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Financial Market
A financial market is a market in which people trade financial securities and derivatives at low transaction costs. Some of the securities include stocks and bonds, raw materials and precious metals, which are known in the financial markets as commodities. The term "market" is sometimes used for what are more strictly ''exchanges'', organizations that facilitate the trade in financial securities, e.g., a stock exchange or commodity exchange. This may be a physical location (such as the New York Stock Exchange (NYSE), London Stock Exchange (LSE), JSE Limited (JSE), Bombay Stock Exchange (BSE) or an electronic system such as NASDAQ. Much trading of stocks takes place on an exchange; still, corporate actions (merger, spinoff) are outside an exchange, while any two companies or people, for whatever reason, may agree to sell the stock from the one to the other without using an exchange. Trading of currencies and bonds is largely on a bilateral basis, although some bond ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Black–Scholes Model
The Black–Scholes or Black–Scholes–Merton model is a mathematical model for the dynamics of a financial market containing derivative investment instruments. From the parabolic partial differential equation in the model, known as the Black–Scholes equation, one can deduce the Black–Scholes formula, which gives a theoretical estimate of the price of European-style options and shows that the option has a ''unique'' price given the risk of the security and its expected return (instead replacing the security's expected return with the risk-neutral rate). The equation and model are named after economists Fischer Black and Myron Scholes; Robert C. Merton, who first wrote an academic paper on the subject, is sometimes also credited. The main principle behind the model is to hedge the option by buying and selling the underlying asset in a specific way to eliminate risk. This type of hedging is called "continuously revised delta hedging" and is the basis of more complicated ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
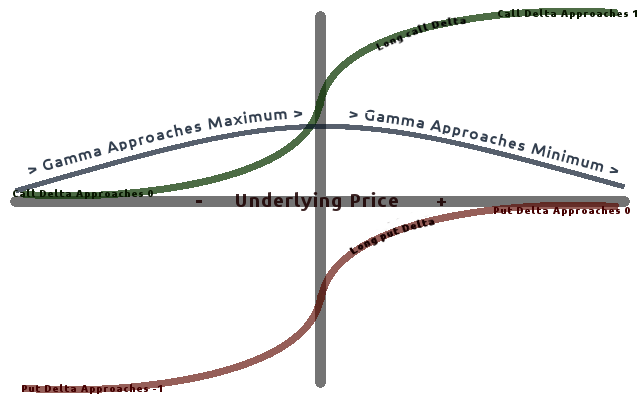
Delta Hedging
In finance, delta neutral describes a portfolio of related financial securities, in which the portfolio value remains unchanged when small changes occur in the value of the underlying security. Such a portfolio typically contains options and their corresponding underlying securities such that positive and negative delta components offset, resulting in the portfolio's value being relatively insensitive to changes in the value of the underlying security. A related term, delta hedging is the process of setting or keeping the delta of a portfolio as close to zero as possible. In practice, maintaining a zero delta is very complex because there are risks associated with re-hedging on large movements in the underlying stock's price, and research indicates portfolios tend to have lower cash flows if re-hedged too frequently.De Weert F. pp. 74-81 Nomenclature \Delta The sensitivity of an option's value to a change in the underlying stock's price. V_0 The initial value of the opti ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Partial Derivative
In mathematics, a partial derivative of a function of several variables is its derivative with respect to one of those variables, with the others held constant (as opposed to the total derivative, in which all variables are allowed to vary). Partial derivatives are used in vector calculus and differential geometry. The partial derivative of a function f(x, y, \dots) with respect to the variable x is variously denoted by It can be thought of as the rate of change of the function in the x-direction. Sometimes, for z=f(x, y, \ldots), the partial derivative of z with respect to x is denoted as \tfrac. Since a partial derivative generally has the same arguments as the original function, its functional dependence is sometimes explicitly signified by the notation, such as in: :f'_x(x, y, \ldots), \frac (x, y, \ldots). The symbol used to denote partial derivatives is ∂. One of the first known uses of this symbol in mathematics is by Marquis de Condorcet from 1770, who used it ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Financial Risk Management
Financial risk management is the practice of protecting Value (economics), economic value in a business, firm by using financial instruments to manage exposure to financial risk - principally operational risk, credit risk and market risk, with more specific variants as listed aside. As for risk management more generally, financial risk management requires identifying its sources, measuring it, and the plans to address them. See for an overview. Financial risk management as a "science" can be said to have been born with modern portfolio theory, particularly as initiated by Professor Harry Markowitz in 1952 with his article, "Portfolio Selection"; see . Financial risk management can be qualitative and quantitative. As a specialization of risk management, financial risk management focuses on when and how to Hedge (finance), hedge using financial instruments to manage costly exposures to risk. *In the banking sector worldwide, the Basel Accords are generally adopted by internatio ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Schwarz's Theorem
In mathematics, the symmetry of second derivatives (also called the equality of mixed partials) refers to the possibility of interchanging the order of taking partial derivatives of a function :f\left(x_1,\, x_2,\, \ldots,\, x_n\right) of ''n'' variables without changing the result under certain conditions (see below). The symmetry is the assertion that the second-order partial derivatives satisfy the identity :\frac \left( \frac \right) \ = \ \frac \left( \frac \right) so that they form an ''n'' × ''n'' symmetric matrix, known as the function's Hessian matrix. This is sometimes known as Schwarz's theorem, Clairaut's theorem, or Young's theorem. In the context of partial differential equations it is called the Schwarz integrability condition. Formal expressions of symmetry In symbols, the symmetry may be expressed as: :\frac \left( \frac \right) \ = \ \frac \left( \frac \right) \qquad\text\qquad \frac \ =\ \frac . Another n ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |