|
Gnomon Workshop
A gnomon (; ) is the part of a sundial that casts a shadow. The term is used for a variety of purposes in mathematics and other fields. History A painted stick dating from 2300 BC that was excavated at the astronomical site of Taosi is the oldest gnomon known in China. The gnomon was widely used in ancient China from the second century BC onward in order to determine the changes in seasons, orientation, and geographical latitude. The ancient Chinese used shadow measurements for creating calendars that are mentioned in several ancient texts. According to the collection of Zhou Chinese poetic anthologies '' Classic of Poetry'', one of the distant ancestors of King Wen of the Zhou dynasty used to measure gnomon shadow lengths to determine the orientation around the 14th century BC. The ancient Greek philosopher Anaximander (610–546 BC) is credited with introducing this Babylonian instrument to the Ancient Greeks. The ancient Greek mathematician and astronomer Oenopides used ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Sundial Taganrog
A sundial is a horological device that tells the time of day (referred to as civil time in modern usage) when direct sunlight shines by the apparent position of the Sun in the sky. In the narrowest sense of the word, it consists of a flat plate (the ''dial'') and a gnomon, which casts a shadow onto the dial. As the Sun appears to move through the sky, the shadow aligns with different hour-lines, which are marked on the dial to indicate the time of day. The ''style'' is the time-telling edge of the gnomon, though a single point or ''nodus'' may be used. The gnomon casts a broad shadow; the shadow of the style shows the time. The gnomon may be a rod, wire, or elaborately decorated metal casting. The style must be parallel to the axis of the Earth's rotation for the sundial to be accurate throughout the year. The style's angle from horizontal is equal to the sundial's geographical latitude. The term ''sundial'' can refer to any device that uses the Sun's altitude or azimuth ( ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Figurate Number
The term figurate number is used by different writers for members of different sets of numbers, generalizing from triangular numbers to different shapes (polygonal numbers) and different dimensions (polyhedral numbers). The term can mean * polygonal number * a number represented as a discrete -dimensional regular geometry, geometric pattern of -dimensional Ball (mathematics), balls such as a polygonal number (for ) or a polyhedral number (for ). * a member of the subset of the sets above containing only triangular numbers, pyramidal numbers, and their analogs in other dimensions. Terminology Some kinds of figurate number were discussed in the 16th and 17th centuries under the name "figural number". In historical works about Greek mathematics the preferred term used to be ''figured number''. In a use going back to Jacob Bernoulli's Ars Conjectandi, the term ''figurate number'' is used for triangular numbers made up of successive integers, tetrahedral numbers made up of successi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Leonardo Ximenes
Leonardo Ximenes (27 December 1716 – 3 May 1786) was a famous Italian Jesuit '' ''(1937). , , and from |
Paolo Toscanelli
Paolo dal Pozzo Toscanelli (1397 – 10 May 1482) was an Italian mathematician, astronomer,, pp. 333–335 and cosmographer. Life Paolo dal Pozzo Toscanelli was born in Florence, the son of the physician Domenico Toscanelli. There is no precise information on his education and background. Gustavo Uzielli claimed in 1894 that Toscanelli studied at the University of Padua, but modern authors consider this pure conjecture. Toscanelli is noted for his observations of comets. Among these was the comet of 1456, which was to be named Halley’s Comet after Edmond Halley predicted its return in 1759. Thanks to his long life, his intelligence and his wide interests, Toscanelli was one of the central figures in the intellectual and cultural history of Renaissance Florence in its early years. His circle of friends included Filippo Brunelleschi, the architect of the Florence Cathedral, and the philosopher Marsilio Ficino. He knew the mathematician, writer and architect Leon Batti ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Ibn Yunus
Abu al-Hasan 'Ali ibn 'Abd al-Rahman ibn Ahmad ibn Yunus al-Sadafi al-Misri (Arabic: ابن يونس; c. 950 – 1009) was an important Egyptians, Egyptian astronomer and Islamic mathematics, mathematician, whose works are noted for being ahead of their time, having been based on meticulous calculations and attention to detail. The crater Ibn Yunus (crater), Ibn Yunus on the Moon is named after him. Life Information regarding his early life and education is uncertain. He was born in Egypt between 950 and 952 and came from a respected family in Fostat, Fustat. His father was a historian, biographer, and scholar of hadith, who wrote two volumes about the history of Egypt—one about the Egyptians and one based on traveller commentary on Egypt. A prolific writer, Ibn Yunus' father has been described as "Egypt's most celebrated early historian and first known compiler of a biographical dictionary devoted exclusively to Egyptians". His great-grandfather had been an associate of the no ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Zhoubi Suanjing
The ''Zhoubi Suanjing'' () is one of the oldest Chinese mathematical texts. "Zhou" refers to the ancient Zhou dynasty (1046–256 BCE); "Bì" literally means "thigh", but in the book refers to the gnomon of a sundial. The book is dedicated to astronomical observation and calculation. ''Suan Jing'' or "classic of arithmetics" were appended in later time to honor the achievement of the book in mathematics. This book dates from the period of the Zhou dynasty, yet its compilation and addition of materials continued into the Han dynasty (202 BCE–220 CE). It is an anonymous collection of 246 problems encountered by the Duke of Zhou and his astronomer and mathematician, Shang Gao. Each question has stated their numerical answer and corresponding arithmetic algorithm. The book also makes use of the Pythagorean Theorem on various occasions and might also contain a geometric proof of the theorem for the case of the 3-4-5 triangle (but the procedure works for a general right triangle ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Geodesy
Geodesy ( ) is the Earth science of accurately measuring and understanding Earth's figure (geometric shape and size), orientation in space, and gravity. The field also incorporates studies of how these properties change over time and equivalent measurements for other planets (known as '' planetary geodesy''). Geodynamical phenomena, including crustal motion, tides and polar motion, can be studied by designing global and national control networks, applying space geodesy and terrestrial geodetic techniques and relying on datums and coordinate systems. The job title is geodesist or geodetic surveyor. History Definition The word geodesy comes from the Ancient Greek word ''geodaisia'' (literally, "division of Earth"). It is primarily concerned with positioning within the temporally varying gravitational field. Geodesy in the German-speaking world is divided into "higher geodesy" ( or ), which is concerned with measuring Earth on the global scale, and "practical geodes ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
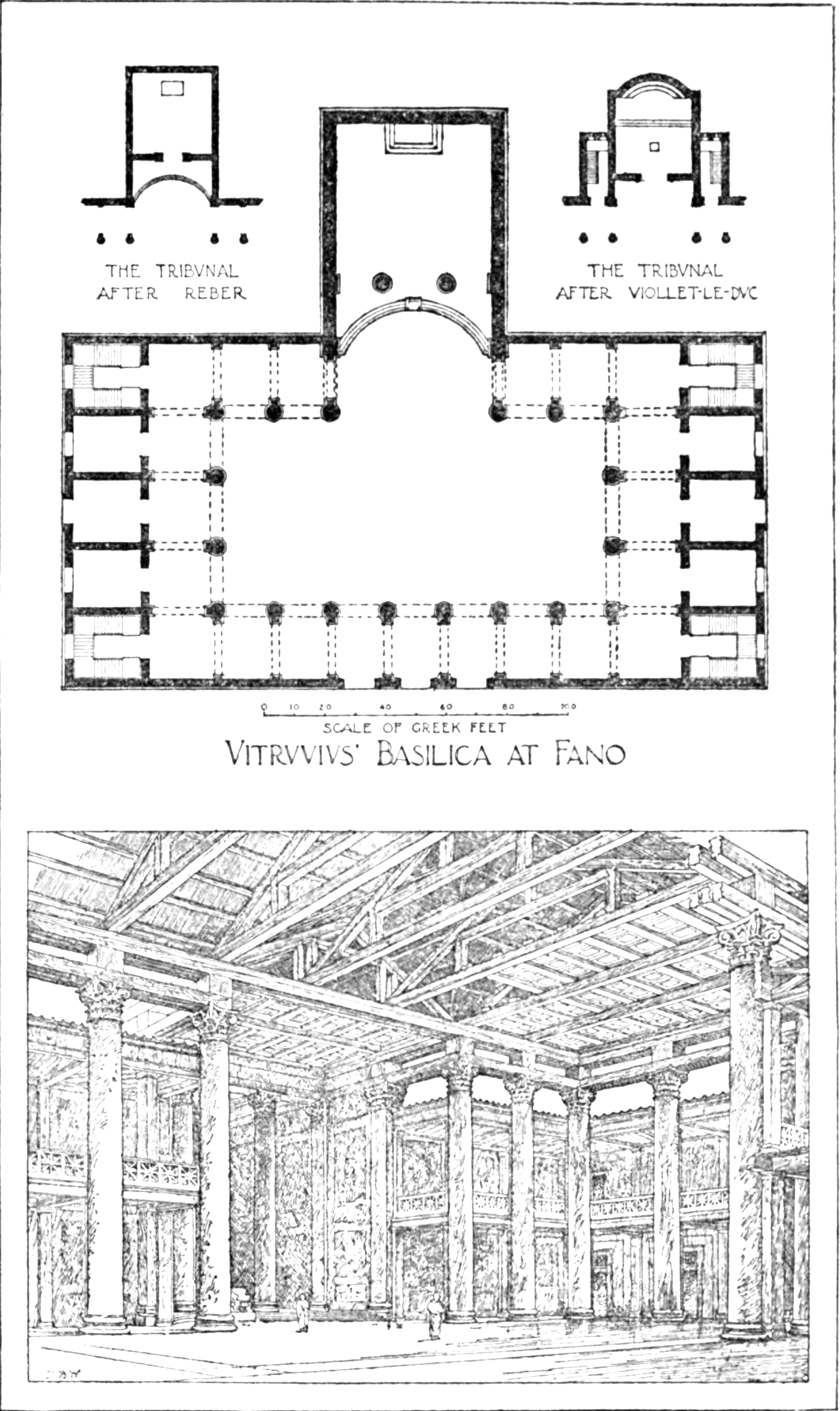
Vitruvius
Vitruvius (; c. 80–70 BC – after c. 15 BC) was a Roman architect and engineer during the 1st century BC, known for his multi-volume work entitled ''De architectura''. He originated the idea that all buildings should have three attributes: , , and ("strength", "utility", and "beauty"). These principles were later widely adopted in Roman architecture. His discussion of perfect proportion in architecture and the human body led to the famous Renaissance drawing of the ''Vitruvian Man'' by Leonardo da Vinci. Little is known about Vitruvius' life, but by his own descriptionDe Arch. Book 1, preface. section 2. he served as an artilleryman, the third class of arms in the Roman military offices. He probably served as a senior officer of artillery in charge of ''doctores ballistarum'' (artillery experts) and ''libratores'' who actually operated the machines. As an army engineer he specialized in the construction of ''ballista'' and '' scorpio'' artillery war machines for sieges. ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Marcus Vitruvius Pollio
Vitruvius (; c. 80–70 BC – after c. 15 BC) was a Roman architect and engineer during the 1st century BC, known for his multi-volume work entitled ''De architectura''. He originated the idea that all buildings should have three attributes: , , and ("strength", "utility", and "beauty"). These principles were later widely adopted in Roman architecture. His discussion of perfect proportion in architecture and the human body led to the famous Renaissance drawing of the ''Vitruvian Man'' by Leonardo da Vinci. Little is known about Vitruvius' life, but by his own descriptionDe Arch. Book 1, preface. section 2. he served as an artilleryman, the third class of arms in the Roman military offices. He probably served as a senior officer of artillery in charge of ''doctores ballistarum'' (artillery experts) and ''libratores'' who actually operated the machines. As an army engineer he specialized in the construction of ''ballista'' and '' scorpio'' artillery war machines for sieges. ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Square Numbers
In mathematics, a square number or perfect square is an integer that is the square of an integer; in other words, it is the product of some integer with itself. For example, 9 is a square number, since it equals and can be written as . The usual notation for the square of a number is not the product , but the equivalent exponentiation Exponentiation is a mathematical operation, written as , involving two numbers, the '' base'' and the ''exponent'' or ''power'' , and pronounced as " (raised) to the (power of) ". When is a positive integer, exponentiation corresponds to re ... , usually pronounced as " squared". The name ''square'' number comes from the name of the shape. The unit of area is defined as the area of a unit square (). Hence, a square with side length has area . If a square number is represented by ''n'' points, the points can be arranged in rows as a square each side of which has the same number of points as the square root of ''n''; thus, square numbers ar ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Figurate Number
The term figurate number is used by different writers for members of different sets of numbers, generalizing from triangular numbers to different shapes (polygonal numbers) and different dimensions (polyhedral numbers). The term can mean * polygonal number * a number represented as a discrete -dimensional regular geometry, geometric pattern of -dimensional Ball (mathematics), balls such as a polygonal number (for ) or a polyhedral number (for ). * a member of the subset of the sets above containing only triangular numbers, pyramidal numbers, and their analogs in other dimensions. Terminology Some kinds of figurate number were discussed in the 16th and 17th centuries under the name "figural number". In historical works about Greek mathematics the preferred term used to be ''figured number''. In a use going back to Jacob Bernoulli's Ars Conjectandi, the term ''figurate number'' is used for triangular numbers made up of successive integers, tetrahedral numbers made up of successi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |