|
Gibbard–Satterthwaite Theorem
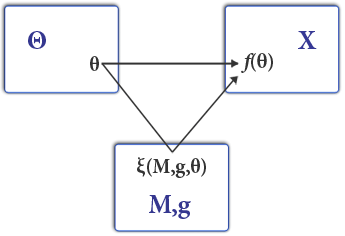
The Gibbard–Satterthwaite theorem is a theorem in social choice theory. It was first conjectured by the philosopher Michael Dummett and the mathematician Robin Farquharson in 1961 and then proved independently by the philosopher Allan Gibbard in 1973 and economist Mark Satterthwaite in 1975. It deals with deterministic ordinal electoral systems that choose a single winner, and shows that for every voting rule of this form, at least one of the following three things must hold: # The rule is dictatorial, i.e. there exists a distinguished voter who can choose the winner; or # The rule limits the possible outcomes to two alternatives only; or # The rule is not straightforward, i.e. there is no single always-best strategy (one that does not depend on other voters' preferences or behavior). Gibbard's proof of the theorem is more general and covers processes of collective decision that may not be ordinal, such as cardinal voting. Gibbard's 1978 theorem and Hylland's theorem are e ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Social Choice Theory
Social choice theory is a branch of welfare economics that extends the Decision theory, theory of rational choice to collective decision-making. Social choice studies the behavior of different mathematical procedures (social welfare function, social welfare functions) used to combine individual preferences into a coherent whole.Amartya Sen (2008). "Social Choice". ''The New Palgrave Dictionary of Economics'', 2nd EditionAbstract & TOC./ref> It contrasts with political science in that it is a Normative economics, normative field that studies how a society can make good decisions, whereas political science is a Positive economics, descriptive field that observes how societies actually do make decisions. While social choice began as a branch of economics and decision theory, it has since received substantial contributions from mathematics, philosophy, political science, and game theory. Real-world examples of social choice rules include constitution, constitutions and Parliamentary ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Arrow's Impossibility Theorem
Arrow's impossibility theorem is a key result in social choice theory showing that no ranked-choice procedure for group decision-making can satisfy the requirements of rational choice. Specifically, Arrow showed no such rule can satisfy the independence of irrelevant alternatives axiom. This is the principle that a choice between two alternatives and should not depend on the quality of some third, unrelated option, . The result is often cited in discussions of voting rules, where it shows no ranked voting rule to eliminate the spoiler effect. This result was first shown by the Marquis de Condorcet, whose voting paradox showed the impossibility of logically-consistent majority rule; Arrow's theorem generalizes Condorcet's findings to include non-majoritarian rules like collective leadership or consensus decision-making. While the impossibility theorem shows all ranked voting rules must have spoilers, the frequency of spoilers differs dramatically by rule. Plurality-rule me ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Voting Theory
Social choice theory is a branch of welfare economics that extends the theory of rational choice to collective decision-making. Social choice studies the behavior of different mathematical procedures ( social welfare functions) used to combine individual preferences into a coherent whole.Amartya Sen (2008). "Social Choice". ''The New Palgrave Dictionary of Economics'', 2nd EditionAbstract & TOC./ref> It contrasts with political science in that it is a normative field that studies how a society can make good decisions, whereas political science is a descriptive field that observes how societies actually do make decisions. While social choice began as a branch of economics and decision theory, it has since received substantial contributions from mathematics, philosophy, political science, and game theory. Real-world examples of social choice rules include constitutions and parliamentary procedures for voting on laws, as well as electoral systems; as such, the field is occasionall ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Strategic Voting
Strategic or tactical voting is voting in consideration of possible ballots cast by other voters in order to maximize one's satisfaction with the election's results. Gibbard's theorem shows that no voting system has a single "always-best" strategy, i.e. one that always maximizes a voter's satisfaction with the result, regardless of other voters' ballots. This implies all voting systems can sometimes encourage voters to strategize. However, weaker guarantees can be shown under stronger conditions. Examples include one-dimensional preferences (where the median rule is strategyproof) and dichotomous preferences (where approval or score voting are strategyproof). With large electoral districts, party list methods tend to be difficult to manipulate in the absence of an electoral threshold. However, biased apportionment methods can create opportunities for strategic voting, as can small electoral districts (e.g. those used most often with the single transferable vote). Proportio ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Condorcet Cycle
In social choice theory, Condorcet's voting paradox is a fundamental discovery by the Marquis de Condorcet that majority rule is inherently self-contradictory. The result implies that it is logically impossible for any voting system to guarantee that a winner will have support from a majority of voters; for example, there can be rock-paper-scissors scenarios where a majority of voters will prefer A to B, B to C, and also C to A, even if every voter's individual preferences are rational and avoid self-contradiction. Examples of Condorcet's paradox are called Condorcet cycles or cyclic ties. In such a cycle, every possible choice is rejected by the electorate in favor of another alternative, who is preferred by more than half of all voters. Thus, any attempt to ground social decision-making in majoritarianism must accept such self-contradictions (commonly called spoiler effects). Systems that attempt to do so, while minimizing the rate of such self-contradictions, are called Condo ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Noam Nisan
Noam Nisan (; born June 20, 1961) is an Israeli computer scientist and professor of computer science at the Hebrew University of Jerusalem. He is known for his research in computational complexity theory and algorithmic game theory. Biography Nisan did his undergraduate studies at the Hebrew University, graduating in 1984. He went to the University of California, Berkeley, for graduate school, and received a Ph.D. in 1988 under the supervision of Richard Karp. After postdoctoral studies at the Massachusetts Institute of Technology he joined the Hebrew University faculty in 1990.Curriculum vitae retrieved 2012-03-01. Selected publications Nisan is the author of[...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mechanism Design
Mechanism design (sometimes implementation theory or institution design) is a branch of economics and game theory. It studies how to construct rules—called Game form, mechanisms or institutions—that produce good outcomes according to Social welfare function, some predefined metric, even when the designer does not know the players' true preferences or what information they have. Mechanism design thus focuses on the study of solution concepts for a class of private-information games. Mechanism design has broad applications, including traditional domains of economics such as market design, but also political science (through voting theory). It is a foundational component in the operation of the internet, being used in networked systems (such as inter-domain routing), e-commerce, and Sponsored search auction, advertisement auctions by Facebook and Google. Because it starts with the end of the game (a particular result), then works backwards to find a game that implements it, it ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Tactical Voting
Strategic or tactical voting is voting in consideration of possible ballots cast by other voters in order to maximize one's satisfaction with the election's results. Gibbard's theorem shows that no voting system has a single "always-best" strategy, i.e. one that always maximizes a voter's satisfaction with the result, regardless of other voters' ballots. This implies all voting systems can sometimes encourage voters to strategize. However, weaker guarantees can be shown under stronger conditions. Examples include one-dimensional preferences (where the median rule is strategyproof) and dichotomous preferences (where approval or score voting are strategyproof). With large electoral districts, party list methods tend to be difficult to manipulate in the absence of an electoral threshold. However, biased apportionment methods can create opportunities for strategic voting, as can small electoral districts (e.g. those used most often with the single transferable vote). Proporti ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Duncan Black
Duncan Black, FBA (23 May 1908 – 14 January 1991) was a Scottish economist who laid the foundations of social choice theory. In particular he was responsible for unearthing the work of many early political scientists, including Charles Lutwidge Dodgson, and was responsible for the Black electoral system, a Condorcet method whereby, in the absence of a Condorcet winner (e.g. due to a cycle), the Borda winner is chosen. Biography Black was born in Motherwell, Scotland, an industrial town south east of Glasgow, to a working-class family. He graduated from the Dalziel High School in Motherwell and then studied mathematics and physics at the University of Glasgow. He then enrolled for a degree in economics and politics which he finished with first class honours in 1932. He started teaching at the newly formed Dundee School of Economics (later part of the University of Dundee). There Black was influenced by his colleague Ronald Coase, originator of the Theory of the Firm. He ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Lewis Carroll
Charles Lutwidge Dodgson (27 January 1832 – 14 January 1898), better known by his pen name Lewis Carroll, was an English author, poet, mathematician, photographer and reluctant Anglicanism, Anglican deacon. His most notable works are ''Alice's Adventures in Wonderland'' (1865) and its sequel ''Through the Looking-Glass'' (1871). He was noted for his facility with word play, logic, and fantasy. His poems ''Jabberwocky'' (1871) and ''The Hunting of the Snark'' (1876) are classified in the genre of literary nonsense. Some of Alice's nonsensical wonderland logic reflects his published work on mathematical logic. Carroll came from a family of high-church Anglicanism, Anglicans, and pursued his clerical training at Christ Church, Oxford, where he lived for most of his life as a scholar, teacher and (necessarily for his academic fellowship at the time) Anglican deacon. Alice Liddell – a daughter of Henry Liddell, the Dean of Christ Church, Oxford, Dean of Christ Church – is wide ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
The American Mathematical Monthly
''The American Mathematical Monthly'' is a peer-reviewed scientific journal of mathematics. It was established by Benjamin Finkel in 1894 and is published by Taylor & Francis on behalf of the Mathematical Association of America. It is an expository journal intended for a wide audience of mathematicians, from undergraduate students to research professionals. Articles are chosen on the basis of their broad interest and reviewed and edited for quality of exposition as well as content. The editor-in-chief is Vadim Ponomarenko (San Diego State University). The journal gives the Lester R. Ford Award annually to "authors of articles of expository excellence" published in the journal. Editors-in-chief The following persons are or have been editor-in-chief: See also *''Mathematics Magazine'' *''Notices of the American Mathematical Society ''Notices of the American Mathematical Society'' is the membership journal of the American Mathematical Society (AMS), published monthly except f ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Dictatorship Mechanism
In social choice theory, a dictatorship mechanism is a degenerate voting rule or mechanism where the result depends on one person's. A serial dictatorship is similar, but also designates a series of "backup dictators", who break ties in the original dictator's choices when the dictator is indifferent. Formal definition Non-dictatorship is one of the necessary conditions in Arrow's impossibility theorem.''Game Theory'' Second Edition Guillermo Owen Ch 6 pp124-5 Axiom 5 Academic Press, 1982 In ''Social Choice and Individual Values'', Kenneth Arrow defines non-dictatorship as: :There is no voter i in such that, for every set of orderings in the domain of the constitution, and every pair of social states ''x'' and ''y'', ''x \succeq_i y'' implies x \succeq y. Unsurprisingly, a dictatorship is a rule that does not satisfy non-dictatorship. Anonymous voting rules automatically satisfy non-dictatorship (so long as there is more than one voter). Serial dictatorship When the dictator ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |