|
Generalized F-mean
A generalization is a form of abstraction whereby common properties of specific instances are formulated as general concepts or claims. Generalizations posit the existence of a domain or set of elements, as well as one or more common characteristics shared by those elements (thus creating a conceptual model). As such, they are the essential basis of all valid deductive inferences (particularly in logic, mathematics and science), where the process of verification is necessary to determine whether a generalization holds true for any given situation. Generalization can also be used to refer to the process of identifying the parts of a whole, as belonging to the whole. The parts, which might be unrelated when left on their own, may be brought together as a group, hence belonging to the whole by establishing a common relation between them. However, the parts cannot be generalized into a whole—until a common relation is established among ''all'' parts. This does not mean that the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Abstraction
Abstraction in its main sense is a conceptual process wherein general rules and concepts are derived from the usage and classification of specific examples, literal ("real" or " concrete") signifiers, first principles, or other methods. "An abstraction" is the outcome of this process—a concept that acts as a common noun for all subordinate concepts and connects any related concepts as a ''group'', ''field'', or ''category''.Suzanne K. Langer (1953), ''Feeling and Form: a theory of art developed from Philosophy in a New Key'' p. 90: " Sculptural form is a powerful abstraction from actual objects and the three-dimensional space which we construe ... through touch and sight." Conceptual abstractions may be formed by filtering the information content of a concept or an observable phenomenon, selecting only those aspects which are relevant for a particular purpose. For example, abstracting a leather soccer ball to the more general idea of a ball selects only the information o ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Geospatial
Geographic data and information is defined in the ISO/TC 211 series of standards as data and information having an implicit or explicit association with a location relative to Earth (a geographic location or geographic position). It is also called geospatial data and information, georeferenced data and information, as well as geodata and geoinformation. Approximately 90% of government sourced data has a location component. Location information (known by the many names mentioned here) is stored in a geographic information system (GIS). There are also many different types of geodata, including vector files, raster files, geographic databases, web files, and multi-temporal data. Fields of study Geographic data and information are the subject of a number of overlapping fields of study, mainly: * Geocomputation * Geographic information science * Geoinformatics * Geomatics * Geovisualization This is in addition to other more specific branches, such as: * Cartography * Geode ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
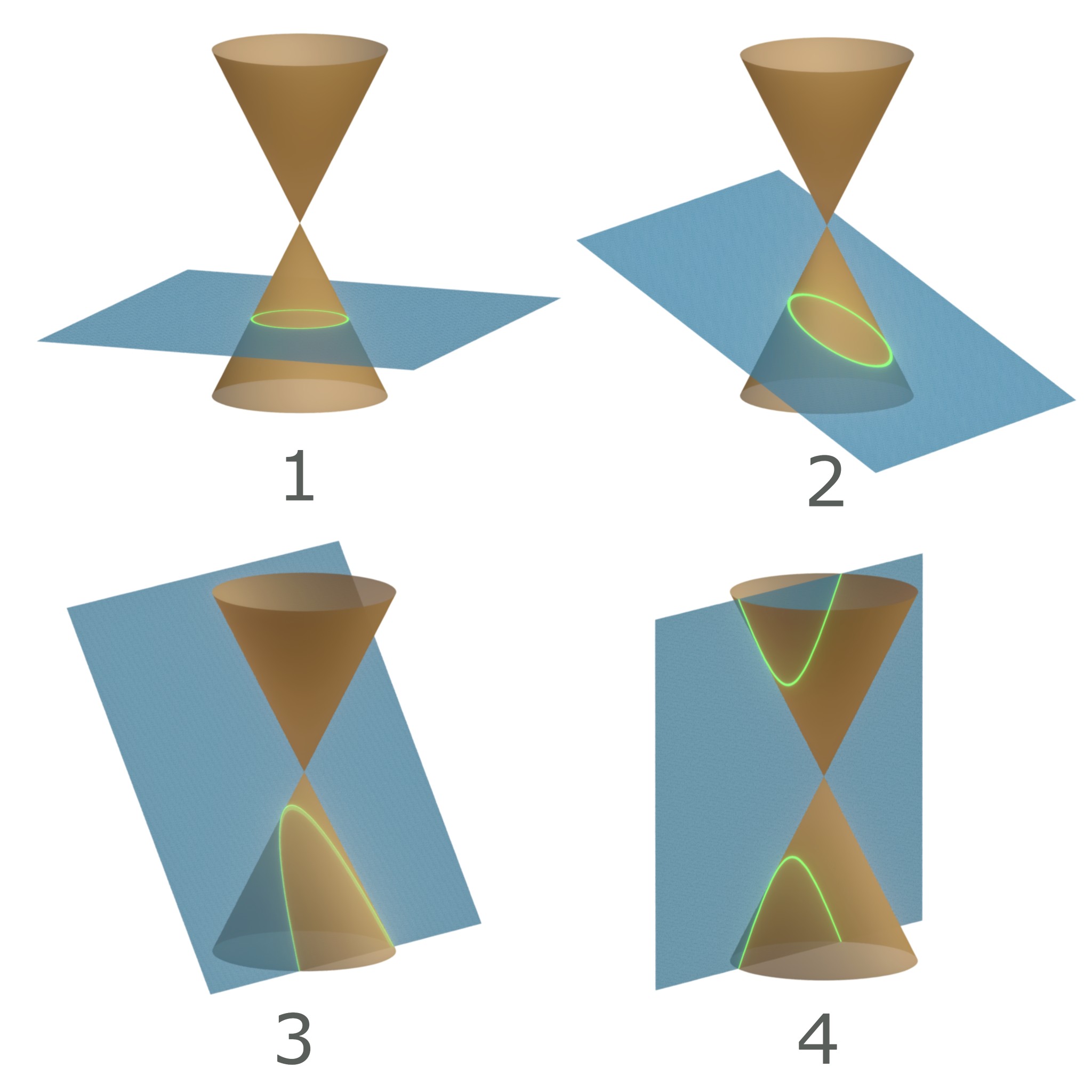
Conic Section
In mathematics, a conic section, quadratic curve or conic is a curve obtained as the intersection of the surface of a cone with a plane. The three types of conic section are the hyperbola, the parabola, and the ellipse; the circle is a special case of the ellipse, though historically it was sometimes called a fourth type. The ancient Greek mathematicians studied conic sections, culminating around 200 BC with Apollonius of Perga's systematic work on their properties. The conic sections in the Euclidean plane have various distinguishing properties, many of which can be used as alternative definitions. One such property defines a non-circular conic to be the set of those points whose distances to some particular point, called a '' focus'', and some particular line, called a ''directrix'', are in a fixed ratio, called the '' eccentricity''. The type of conic is determined by the value of the eccentricity. In analytic geometry, a conic may be defined as a plane algebrai ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
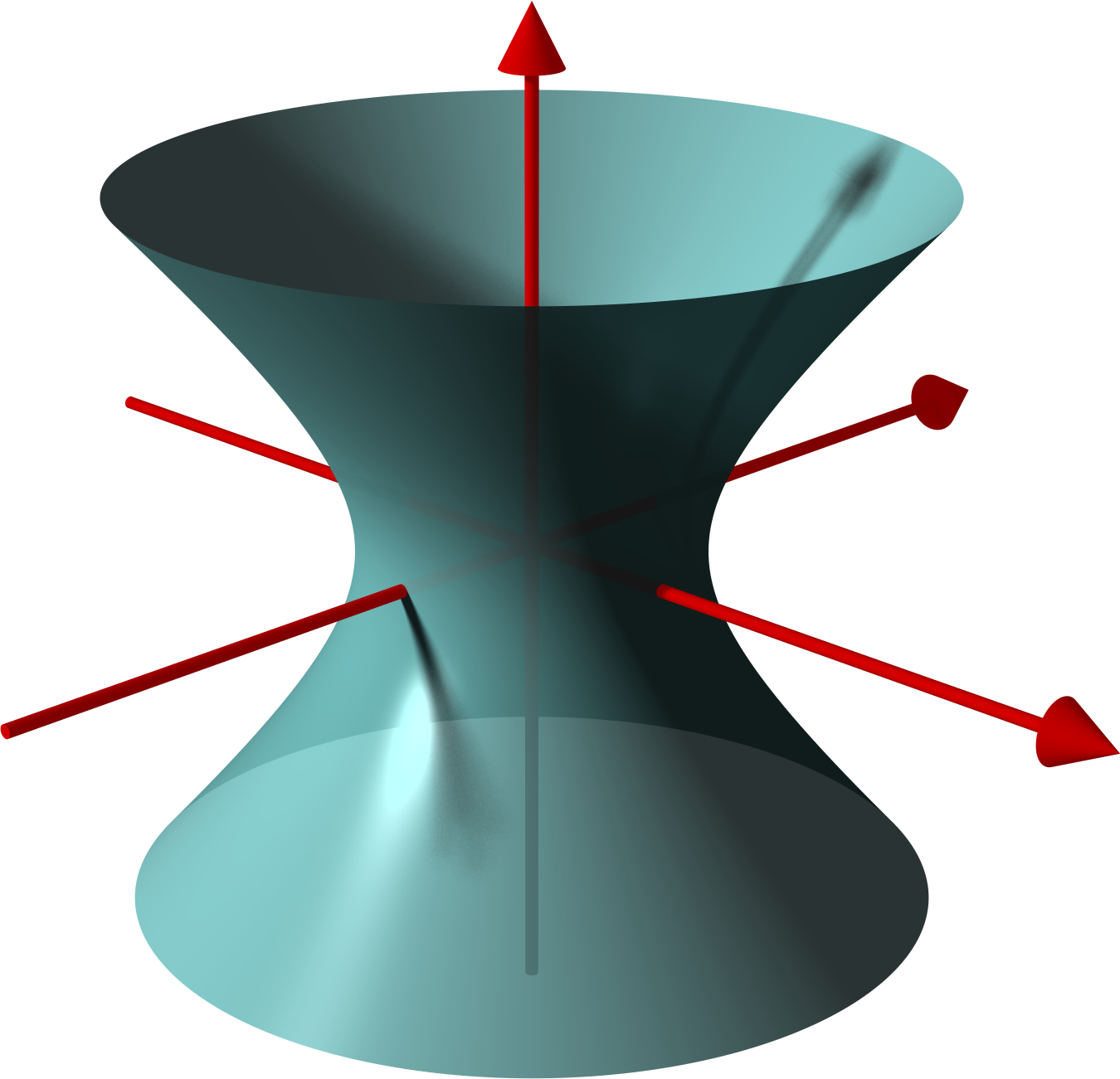
Hyperboloid
In geometry, a hyperboloid of revolution, sometimes called a circular hyperboloid, is the surface generated by rotating a hyperbola around one of its principal axes. A hyperboloid is the surface obtained from a hyperboloid of revolution by deforming it by means of directional scalings, or more generally, of an affine transformation. A hyperboloid is a quadric surface, that is, a surface defined as the zero set of a polynomial of degree two in three variables. Among quadric surfaces, a hyperboloid is characterized by not being a cone or a cylinder, having a center of symmetry, and intersecting many planes into hyperbolas. A hyperboloid has three pairwise perpendicular axes of symmetry, and three pairwise perpendicular planes of symmetry. Given a hyperboloid, one can choose a Cartesian coordinate system such that the hyperboloid is defined by one of the following equations: : + - = 1, or : + - = -1. The coordinate axes are axes of symmetry of the hyperboloid and th ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Paraboloid
In geometry, a paraboloid is a quadric surface that has exactly one axis of symmetry and no center of symmetry. The term "paraboloid" is derived from parabola, which refers to a conic section that has a similar property of symmetry. Every plane section of a paraboloid by a plane parallel to the axis of symmetry is a parabola. The paraboloid is hyperbolic if every other plane section is either a hyperbola, or two crossing lines (in the case of a section by a tangent plane). The paraboloid is elliptic if every other nonempty plane section is either an ellipse, or a single point (in the case of a section by a tangent plane). A paraboloid is either elliptic or hyperbolic. Equivalently, a paraboloid may be defined as a quadric surface that is not a cylinder, and has an implicit equation whose part of degree two may be factored over the complex numbers into two different linear factors. The paraboloid is hyperbolic if the factors are real; elliptic if the factors are complex con ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Ellipsoid
An ellipsoid is a surface that may be obtained from a sphere by deforming it by means of directional scalings, or more generally, of an affine transformation. An ellipsoid is a quadric surface; that is, a surface that may be defined as the zero set of a polynomial of degree two in three variables. Among quadric surfaces, an ellipsoid is characterized by either of the two following properties. Every planar cross section is either an ellipse, or is empty, or is reduced to a single point (this explains the name, meaning "ellipse-like"). It is bounded, which means that it may be enclosed in a sufficiently large sphere. An ellipsoid has three pairwise perpendicular axes of symmetry which intersect at a center of symmetry, called the center of the ellipsoid. The line segments that are delimited on the axes of symmetry by the ellipsoid are called the ''principal axes'', or simply axes of the ellipsoid. If the three axes have different lengths, the figure is a triaxial ellipsoi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Hypersphere
In mathematics, an -sphere or a hypersphere is a topological space that is homeomorphic to a ''standard'' -''sphere'', which is the set of points in -dimensional Euclidean space that are situated at a constant distance from a fixed point, called the ''center''. It is the generalization of an ordinary sphere in the ordinary three-dimensional space. The "radius" of a sphere is the constant distance of its points to the center. When the sphere has unit radius, it is usual to call it the unit -sphere or simply the -sphere for brevity. In terms of the standard norm, the -sphere is defined as : S^n = \left\ , and an -sphere of radius can be defined as : S^n(r) = \left\ . The dimension of -sphere is , and must not be confused with the dimension of the Euclidean space in which it is naturally embedded. An -sphere is the surface or boundary of an -dimensional ball. In particular: *the pair of points at the ends of a (one-dimensional) line segment is a 0-sphere, *a circle, w ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Quadric
In mathematics, a quadric or quadric surface (quadric hypersurface in higher dimensions), is a generalization of conic sections ( ellipses, parabolas, and hyperbolas). It is a hypersurface (of dimension ''D'') in a -dimensional space, and it is defined as the zero set of an irreducible polynomial of degree two in ''D'' + 1 variables; for example, in the case of conic sections. When the defining polynomial is not absolutely irreducible, the zero set is generally not considered a quadric, although it is often called a ''degenerate quadric'' or a ''reducible quadric''. In coordinates , the general quadric is thus defined by the algebraic equationSilvio LevQuadricsin "Geometry Formulas and Facts", excerpted from 30th Edition of ''CRC Standard Mathematical Tables and Formulas'', CRC Press, from The Geometry Center at University of Minnesota : \sum_^ x_i Q_ x_j + \sum_^ P_i x_i + R = 0 which may be compactly written in vector and matrix notation as: : x Q x^\mathrm + P x^\ ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Dimension
In physics and mathematics, the dimension of a mathematical space (or object) is informally defined as the minimum number of coordinates needed to specify any point within it. Thus, a line has a dimension of one (1D) because only one coordinate is needed to specify a point on itfor example, the point at 5 on a number line. A surface, such as the boundary of a cylinder or sphere, has a dimension of two (2D) because two coordinates are needed to specify a point on itfor example, both a latitude and longitude are required to locate a point on the surface of a sphere. A two-dimensional Euclidean space is a two-dimensional space on the plane. The inside of a cube, a cylinder or a sphere is three-dimensional (3D) because three coordinates are needed to locate a point within these spaces. In classical mechanics, space and time are different categories and refer to absolute space and time. That conception of the world is a four-dimensional space but not the one that was fo ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Cube
In geometry, a cube is a three-dimensional solid object bounded by six square faces, facets or sides, with three meeting at each vertex. Viewed from a corner it is a hexagon and its net is usually depicted as a cross. The cube is the only regular hexahedron and is one of the five Platonic solids. It has 6 faces, 12 edges, and 8 vertices. The cube is also a square parallelepiped, an equilateral cuboid and a right rhombohedron a 3- zonohedron. It is a regular square prism in three orientations, and a trigonal trapezohedron in four orientations. The cube is dual to the octahedron. It has cubical or octahedral symmetry. The cube is the only convex polyhedron whose faces are all squares. Orthogonal projections The ''cube'' has four special orthogonal projections, centered, on a vertex, edges, face and normal to its vertex figure. The first and third correspond to the A2 and B2 Coxeter planes. Spherical tiling The cube can also be represented as a spheric ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Hypercube
In geometry, a hypercube is an ''n''-dimensional analogue of a square () and a cube (). It is a closed, compact, convex figure whose 1-skeleton consists of groups of opposite parallel line segments aligned in each of the space's dimensions, perpendicular to each other and of the same length. A unit hypercube's longest diagonal in ''n'' dimensions is equal to \sqrt. An ''n''-dimensional hypercube is more commonly referred to as an ''n''-cube or sometimes as an ''n''-dimensional cube. The term measure polytope (originally from Elte, 1912) is also used, notably in the work of H. S. M. Coxeter who also labels the hypercubes the γn polytopes. The hypercube is the special case of a hyperrectangle (also called an ''n-orthotope''). A ''unit hypercube'' is a hypercube whose side has length one unit. Often, the hypercube whose corners (or ''vertices'') are the 2''n'' points in R''n'' with each coordinate equal to 0 or 1 is called ''the'' unit hypercube. Construction A ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Variable (mathematics)
In mathematics, a variable (from Latin '' variabilis'', "changeable") is a symbol that represents a mathematical object. A variable may represent a number, a vector, a matrix, a function, the argument of a function, a set, or an element of a set. Algebraic computations with variables as if they were explicit numbers solve a range of problems in a single computation. For example, the quadratic formula solves any quadratic equation by substituting the numeric values of the coefficients of that equation for the variables that represent them in the quadratic formula. In mathematical logic, a ''variable'' is either a symbol representing an unspecified term of the theory (a meta-variable), or a basic object of the theory that is manipulated without referring to its possible intuitive interpretation. History In ancient works such as Euclid's ''Elements'', single letters refer to geometric points and shapes. In the 7th century, Brahmagupta used different colours to represe ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |