|
Generalizations Of The Derivative
In mathematics, the derivative is a fundamental construction of differential calculus and admits many possible generalizations within the fields of mathematical analysis, combinatorics, algebra, geometry, etc. Fréchet derivative The Fréchet derivative defines the derivative for general normed vector spaces V, W. Briefly, a function f : U \to W, where U is an open subset of V, is called ''Fréchet differentiable'' at x \in U if there exists a bounded linear operator A:V\to W such that \lim_ \frac = 0. Functions are defined as being differentiable in some open neighbourhood (mathematics), neighbourhood of x, rather than at individual points, as not doing so tends to lead to many Pathological (mathematics), pathological counterexamples. The Fréchet derivative is quite similar to the formula for the derivative found in elementary one-variable calculus, \lim_\frac = A, and simply moves ''A'' to the left hand side. However, the Fréchet derivative ''A'' denotes the function t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mathematics
Mathematics is a field of study that discovers and organizes methods, Mathematical theory, theories and theorems that are developed and Mathematical proof, proved for the needs of empirical sciences and mathematics itself. There are many areas of mathematics, which include number theory (the study of numbers), algebra (the study of formulas and related structures), geometry (the study of shapes and spaces that contain them), Mathematical analysis, analysis (the study of continuous changes), and set theory (presently used as a foundation for all mathematics). Mathematics involves the description and manipulation of mathematical object, abstract objects that consist of either abstraction (mathematics), abstractions from nature orin modern mathematicspurely abstract entities that are stipulated to have certain properties, called axioms. Mathematics uses pure reason to proof (mathematics), prove properties of objects, a ''proof'' consisting of a succession of applications of in ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Partial Derivative
In mathematics, a partial derivative of a function of several variables is its derivative with respect to one of those variables, with the others held constant (as opposed to the total derivative, in which all variables are allowed to vary). Partial derivatives are used in vector calculus and differential geometry. The partial derivative of a function f(x, y, \dots) with respect to the variable x is variously denoted by It can be thought of as the rate of change of the function in the x-direction. Sometimes, for the partial derivative of z with respect to x is denoted as \tfrac. Since a partial derivative generally has the same arguments as the original function, its functional dependence is sometimes explicitly signified by the notation, such as in: f'_x(x, y, \ldots), \frac (x, y, \ldots). The symbol used to denote partial derivatives is ∂. One of the first known uses of this symbol in mathematics is by Marquis de Condorcet from 1770, who used it for partial differ ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Geometric Calculus
In mathematics, geometric calculus extends geometric algebra to include differentiation and integration. The formalism is powerful and can be shown to reproduce other mathematical theories including vector calculus, differential geometry, and differential forms. Differentiation With a geometric algebra given, let a and b be vectors and let F be a multivector-valued function of a vector. The directional derivative of F along b at a is defined as :(\nabla_b F)(a) = \lim_, provided that the limit exists for all b, where the limit is taken for scalar \epsilon. This is similar to the usual definition of a directional derivative but extends it to functions that are not necessarily scalar-valued. Next, choose a set of basis vector In mathematics, a set of elements of a vector space is called a basis (: bases) if every element of can be written in a unique way as a finite linear combination of elements of . The coefficients of this linear combination are referred to as ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Complex Numbers
In mathematics, a complex number is an element of a number system that extends the real numbers with a specific element denoted , called the imaginary unit and satisfying the equation i^= -1; every complex number can be expressed in the form a + bi, where and are real numbers. Because no real number satisfies the above equation, was called an imaginary number by René Descartes. For the complex number is called the , and is called the . The set of complex numbers is denoted by either of the symbols \mathbb C or . Despite the historical nomenclature, "imaginary" complex numbers have a mathematical existence as firm as that of the real numbers, and they are fundamental tools in the scientific description of the natural world. Complex numbers allow solutions to all polynomial equations, even those that have no solutions in real numbers. More precisely, the fundamental theorem of algebra asserts that every non-constant polynomial equation with real or complex coefficients has ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Holomorphic Function
In mathematics, a holomorphic function is a complex-valued function of one or more complex variables that is complex differentiable in a neighbourhood of each point in a domain in complex coordinate space . The existence of a complex derivative in a neighbourhood is a very strong condition: It implies that a holomorphic function is infinitely differentiable and locally equal to its own Taylor series (is '' analytic''). Holomorphic functions are the central objects of study in complex analysis. Though the term '' analytic function'' is often used interchangeably with "holomorphic function", the word "analytic" is defined in a broader sense to denote any function (real, complex, or of more general type) that can be written as a convergent power series in a neighbourhood of each point in its domain. That all holomorphic functions are complex analytic functions, and vice versa, is a major theorem in complex analysis. Holomorphic functions are also sometimes referred to ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Complex Analysis
Complex analysis, traditionally known as the theory of functions of a complex variable, is the branch of mathematical analysis that investigates functions of complex numbers. It is helpful in many branches of mathematics, including algebraic geometry, number theory, analytic combinatorics, and applied mathematics, as well as in physics, including the branches of hydrodynamics, thermodynamics, quantum mechanics, and twistor theory. By extension, use of complex analysis also has applications in engineering fields such as nuclear, aerospace, mechanical and electrical engineering. As a differentiable function of a complex variable is equal to the sum function given by its Taylor series (that is, it is analytic), complex analysis is particularly concerned with analytic functions of a complex variable, that is, '' holomorphic functions''. The concept can be extended to functions of several complex variables. Complex analysis is contrasted with real analysis, which dea ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Parametric Curve
In mathematics, a parametric equation expresses several quantities, such as the coordinates of a point (mathematics), point, as Function (mathematics), functions of one or several variable (mathematics), variables called parameters. In the case of a single parameter, parametric equations are commonly used to express the trajectory of a moving point, in which case, the parameter is often, but not necessarily, time, and the point describes a curve, called a parametric curve. In the case of two parameters, the point describes a Surface (mathematics), surface, called a parametric surface. In all cases, the equations are collectively called a parametric representation, or parametric system, or parameterization (also spelled parametrization, parametrisation) of the object. For example, the equations \begin x &= \cos t \\ y &= \sin t \end form a parametric representation of the unit circle, where is the parameter: A point is on the unit circle if and only if there is a value of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Vector-valued Functions
A vector-valued function, also referred to as a vector function, is a mathematical function of one or more variables whose range is a set of multidimensional vectors or infinite-dimensional vectors. The input of a vector-valued function could be a scalar or a vector (that is, the dimension of the domain could be 1 or greater than 1); the dimension of the function's domain has no relation to the dimension of its range. Example: Helix A common example of a vector-valued function is one that depends on a single real parameter , often representing time, producing a vector as the result. In terms of the standard unit vectors , , of Cartesian , these specific types of vector-valued functions are given by expressions such as \mathbf(t) = f(t)\mathbf + g(t)\mathbf + h(t)\mathbf where , and are the coordinate functions of the parameter , and the domain of this vector-valued function is the intersection of the domains of the functions , , and . It can also be referred to in a d ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
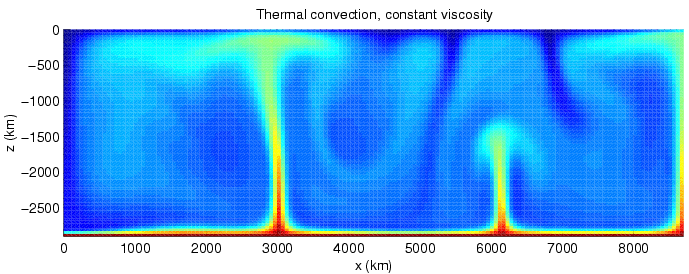
Convective Derivative
Convection is single or multiphase fluid flow that occurs spontaneously through the combined effects of material property heterogeneity and body forces on a fluid, most commonly density and gravity (see buoyancy). When the cause of the convection is unspecified, convection due to the effects of thermal expansion and buoyancy can be assumed. Convection may also take place in soft solids or mixtures where particles can flow. Convective flow may be transient (such as when a multiphase mixture of oil and water separates) or steady state (see convection cell). The convection may be due to gravitational, electromagnetic or fictitious body forces. Heat transfer by natural convection plays a role in the structure of Earth's atmosphere, its oceans, and its mantle. Discrete convective cells in the atmosphere can be identified by clouds, with stronger convection resulting in thunderstorms. Natural convection also plays a role in stellar physics. Convection is often categorise ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Exterior Derivative
On a differentiable manifold, the exterior derivative extends the concept of the differential of a function to differential forms of higher degree. The exterior derivative was first described in its current form by Élie Cartan in 1899. The resulting calculus, known as exterior calculus, allows for a natural, metric-independent generalization of Stokes' theorem, Gauss's theorem, and Green's theorem from vector calculus. If a differential -form is thought of as measuring the flux through an infinitesimal - parallelotope at each point of the manifold, then its exterior derivative can be thought of as measuring the net flux through the boundary of a -parallelotope at each point. Definition The exterior derivative of a differential form of degree (also differential -form, or just -form for brevity here) is a differential form of degree . If is a smooth function (a -form), then the exterior derivative of is the differential of . That is, is the unique -form such that ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Gradient
In vector calculus, the gradient of a scalar-valued differentiable function f of several variables is the vector field (or vector-valued function) \nabla f whose value at a point p gives the direction and the rate of fastest increase. The gradient transforms like a vector under change of basis of the space of variables of f. If the gradient of a function is non-zero at a point p, the direction of the gradient is the direction in which the function increases most quickly from p, and the magnitude of the gradient is the rate of increase in that direction, the greatest absolute directional derivative. Further, a point where the gradient is the zero vector is known as a stationary point. The gradient thus plays a fundamental role in optimization theory, where it is used to minimize a function by gradient descent. In coordinate-free terms, the gradient of a function f(\mathbf) may be defined by: df=\nabla f \cdot d\mathbf where df is the total infinitesimal change in f for a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Total Derivative
In mathematics, the total derivative of a function at a point is the best linear approximation near this point of the function with respect to its arguments. Unlike partial derivatives, the total derivative approximates the function with respect to all of its arguments, not just a single one. In many situations, this is the same as considering all partial derivatives simultaneously. The term "total derivative" is primarily used when is a function of several variables, because when is a function of a single variable, the total derivative is the same as the ordinary derivative of the function. The total derivative as a linear map Let U \subseteq \R^n be an open subset. Then a function f:U \to \R^m is said to be (totally) differentiable at a point a\in U if there exists a linear transformation df_a:\R^n \to \R^m such that :\lim_ \frac=0. The linear map df_a is called the (total) derivative or (total) differential of f at a. Other notations for the total derivative inc ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |