|
Garnier Integrable System
In mathematical physics, the Garnier integrable system, also known as the classical Gaudin model is a classical mechanical system discovered by René Garnier in 1919 by taking the ' Painlevé simplification' or 'autonomous limit' of the Schlesinger equations. It is a classical analogue to the quantum Gaudin model due to Michel Gaudin (similarly, the Schlesinger equations are a classical analogue to the Knizhnik–Zamolodchikov equations). The classical Gaudin models are integrable. They are also a specific case of Hitchin integrable systems, when the algebraic curve that the theory is defined on is the Riemann sphere and the system is tamely ramified. As a limit of the Schlesinger equations The Schlesinger equations are a system of differential equations for n + 2 matrix-valued functions A_i:\mathbb^ \rightarrow \mathrm(m, \mathbb), given by \frac = \frac \qquad \qquad j\neq i \sum_j \frac = 0. The 'autonomous limit' is given by replacing the \lambda_i dependence in t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mathematical Physics
Mathematical physics refers to the development of mathematics, mathematical methods for application to problems in physics. The ''Journal of Mathematical Physics'' defines the field as "the application of mathematics to problems in physics and the development of mathematical methods suitable for such applications and for the formulation of physical theories". An alternative definition would also include those mathematics that are inspired by physics (also known as physical mathematics). Scope There are several distinct branches of mathematical physics, and these roughly correspond to particular historical periods. Classical mechanics The rigorous, abstract and advanced reformulation of Newtonian mechanics adopting the Lagrangian mechanics and the Hamiltonian mechanics even in the presence of constraints. Both formulations are embodied in analytical mechanics and lead to understanding the deep interplay of the notions of symmetry (physics), symmetry and conservation law, con ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Lie Algebra
In mathematics, a Lie algebra (pronounced ) is a vector space \mathfrak g together with an Binary operation, operation called the Lie bracket, an Alternating multilinear map, alternating bilinear map \mathfrak g \times \mathfrak g \rightarrow \mathfrak g, that satisfies the Jacobi identity. The Lie bracket of two vectors x and y is denoted [x,y]. The vector space \mathfrak g together with this operation is a non-associative algebra, meaning that the Lie bracket is not necessarily associative property, associative. Lie algebras are closely related to Lie groups, which are group (mathematics), groups that are also smooth manifolds: any Lie group gives rise to a Lie algebra, which is its tangent space at the identity. Conversely, to any finite-dimensional Lie algebra over real or complex numbers, there is a corresponding connected space, connected Lie group unique up to finite coverings (Lie's third theorem). This Lie group–Lie algebra correspondence, correspondence allows one ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
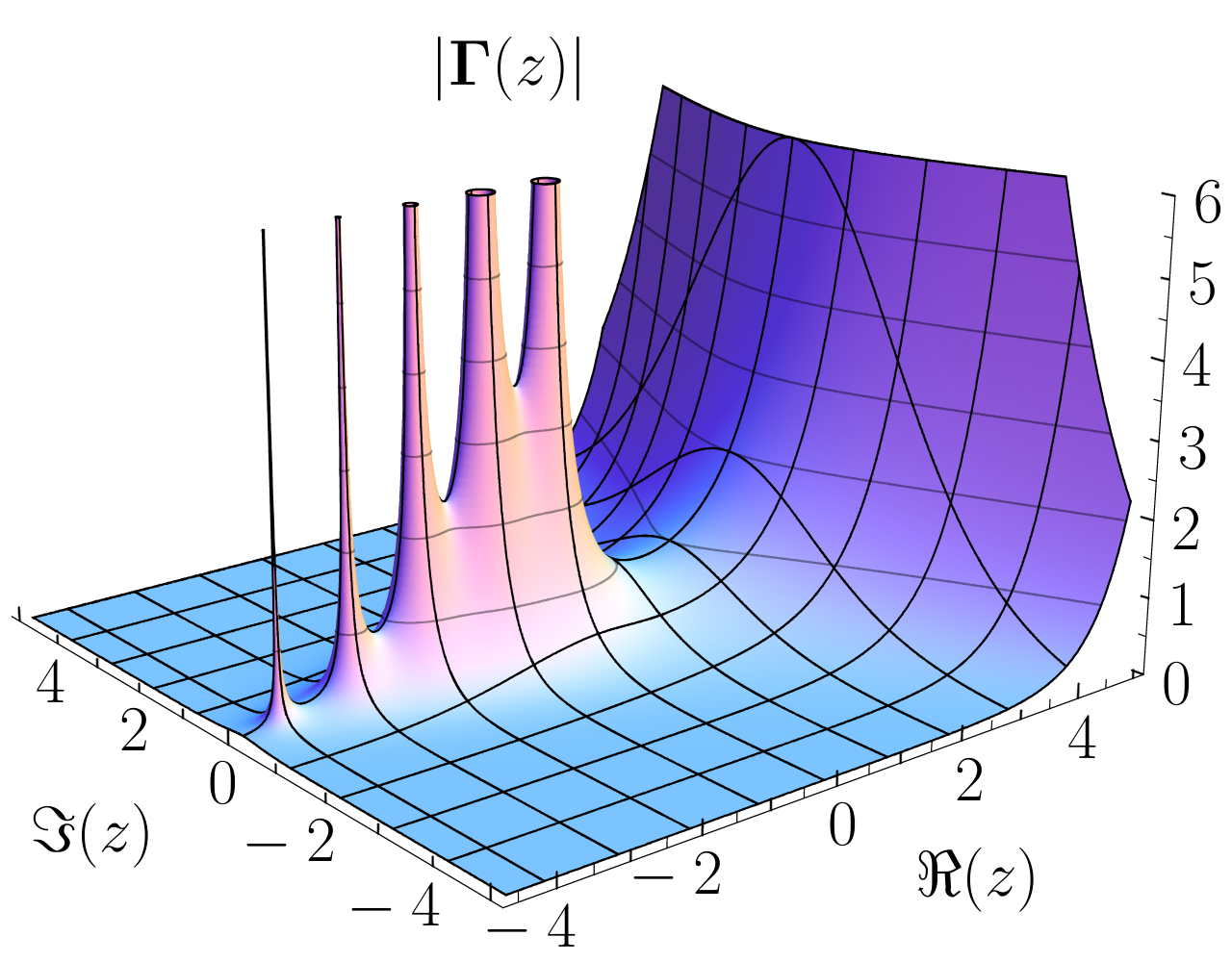
Meromorphic
In the mathematical field of complex analysis, a meromorphic function on an open subset ''D'' of the complex plane is a function that is holomorphic on all of ''D'' ''except'' for a set of isolated points, which are pole (complex analysis), poles of the function. The term comes from the Greek ''meros'' ( μέρος), meaning "part". Every meromorphic function on ''D'' can be expressed as the ratio between two holomorphic functions (with the denominator not constant 0) defined on ''D'': any pole must coincide with a zero of the denominator. Heuristic description Intuitively, a meromorphic function is a ratio of two well-behaved (holomorphic) functions. Such a function will still be well-behaved, except possibly at the points where the denominator of the fraction is zero. If the denominator has a zero at ''z'' and the numerator does not, then the value of the function will approach infinity; if both parts have a zero at ''z'', then one must compare the multiplicity of these zeros ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Lax Pair
In mathematics, in the theory of integrable systems, a Lax pair is a pair of time-dependent matrices or operators that satisfy a corresponding differential equation, called the ''Lax equation''. Lax pairs were introduced by Peter Lax to discuss solitons in continuous media. The inverse scattering transform makes use of the Lax equations to solve such systems. Definition A Lax pair is a pair of matrices or operators L(t), P(t) dependent on time and acting on a fixed Hilbert space, and satisfying Lax's equation: :\frac= ,L/math> where ,LPL-LP is the commutator. Often, as in the example below, P depends on L in a prescribed way, so this is a nonlinear equation for L as a function of t. Isospectral property It can then be shown that the eigenvalues and more generally the spectrum of ''L'' are independent of ''t''. The matrices/operators ''L'' are said to be ''isospectral'' as t varies. The core observation is that the matrices L(t) are all similar by virtue of :L(t)=U(t,s) L( ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Einstein Summation Convention
In mathematics, especially the usage of linear algebra in Mathematical physics, Einstein notation (also known as the Einstein summation convention or Einstein summation notation) is a notational convention that implies summation over a set of indexed terms in a formula, thus achieving brevity. As part of mathematics it is a notational subset of Ricci calculus; however, it is often used in physics applications that do not distinguish between tangent and cotangent spaces. It was introduced to physics by Albert Einstein in 1916. Introduction Statement of convention According to this convention, when an index variable appears twice in a single term and is not otherwise defined (see Free and bound variables), it implies summation of that term over all the values of the index. So where the indices can range over the set , : y = \sum_^3 c_i x^i = c_1 x^1 + c_2 x^2 + c_3 x^3 is simplified by the convention to: : y = c_i x^i The upper indices are not exponents but are indices of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Structure Constant
In mathematics, the structure constants or structure coefficients of an algebra over a field are used to explicitly specify the product of two basis vectors in the algebra as a linear combination. Given the structure constants, the resulting product is bilinear and can be uniquely extended to all vectors in the vector space, thus uniquely determining the product for the algebra. Structure constants are used whenever an explicit form for the algebra must be given. Thus, they are frequently used when discussing Lie algebras in physics, as the basis vectors indicate specific directions in physical space, or correspond to specific particles. Recall that Lie algebras are algebras over a field, with the bilinear product being given by the Lie bracket or commutator. Definition Given a set of basis vectors \ for the underlying vector space of the algebra, the structure constants or structure coefficients c_^ express the multiplication \cdot of pairs of vectors as a linear combinati ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Cartesian Product
In mathematics, specifically set theory, the Cartesian product of two sets ''A'' and ''B'', denoted ''A''×''B'', is the set of all ordered pairs where ''a'' is in ''A'' and ''b'' is in ''B''. In terms of set-builder notation, that is : A\times B = \. A table can be created by taking the Cartesian product of a set of rows and a set of columns. If the Cartesian product is taken, the cells of the table contain ordered pairs of the form . One can similarly define the Cartesian product of ''n'' sets, also known as an ''n''-fold Cartesian product, which can be represented by an ''n''-dimensional array, where each element is an ''n''-tuple. An ordered pair is a 2-tuple or couple. More generally still, one can define the Cartesian product of an indexed family of sets. The Cartesian product is named after René Descartes, whose formulation of analytic geometry gave rise to the concept, which is further generalized in terms of direct product. Examples A deck of cards An ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Coadjoint Orbit
In mathematics, the coadjoint representation K of a Lie group G is the dual of the adjoint representation. If \mathfrak denotes the Lie algebra of G, the corresponding action of G on \mathfrak^*, the dual space to \mathfrak, is called the coadjoint action. A geometrical interpretation is as the action by left-translation on the space of right-invariant 1-forms on G. The importance of the coadjoint representation was emphasised by work of Alexandre Kirillov, who showed that for nilpotent Lie groups G a basic role in their representation theory is played by coadjoint orbits. In the Kirillov method of orbits, representations of G are constructed geometrically starting from the coadjoint orbits. In some sense those play a substitute role for the conjugacy classes of G, which again may be complicated, while the orbits are relatively tractable. Formal definition Let G be a Lie group and \mathfrak be its Lie algebra. Let \mathrm : G \rightarrow \mathrm(\mathfrak) denote the adjoint repres ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Dual Vector Space
In mathematics, any vector space ''V'' has a corresponding dual vector space (or just dual space for short) consisting of all linear forms on ''V'', together with the vector space structure of pointwise addition and scalar multiplication by constants. The dual space as defined above is defined for all vector spaces, and to avoid ambiguity may also be called the . When defined for a topological vector space, there is a subspace of the dual space, corresponding to continuous linear functionals, called the ''continuous dual space''. Dual vector spaces find application in many branches of mathematics that use vector spaces, such as in tensor analysis with finite-dimensional vector spaces. When applied to vector spaces of functions (which are typically infinite-dimensional), dual spaces are used to describe measures, distributions, and Hilbert spaces. Consequently, the dual space is an important concept in functional analysis. Early terms for ''dual'' include ''polarer Raum'' ahn 1 ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Killing Form
In mathematics, the Killing form, named after Wilhelm Killing, is a symmetric bilinear form that plays a basic role in the theories of Lie groups and Lie algebras. Cartan's criteria (criterion of solvability and criterion of semisimplicity) show that Killing form has a close relationship to the semisimplicity of the Lie algebras. History and name The Killing form was essentially introduced into Lie algebra theory by in his thesis. In a historical survey of Lie theory, has described how the term ''"Killing form"'' first occurred in 1951 during one of his own reports for the Séminaire Bourbaki; it arose as a misnomer, since the form had previously been used by Lie theorists, without a name attached. Some other authors now employ the term ''" Cartan-Killing form"''. At the end of the 19th century, Killing had noted that the coefficients of the characteristic equation of a regular semisimple element of a Lie algebra are invariant under the adjoint group, from which it follows tha ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Simple Lie Algebra
In algebra, a simple Lie algebra is a Lie algebra that is non-abelian and contains no nonzero proper ideals. The classification of real simple Lie algebras is one of the major achievements of Wilhelm Killing and Élie Cartan. A direct sum of simple Lie algebras is called a semisimple Lie algebra. A simple Lie group is a connected Lie group whose Lie algebra is simple. Complex simple Lie algebras A finite-dimensional simple complex Lie algebra is isomorphic to either of the following: \mathfrak_n \mathbb, \mathfrak_n \mathbb, \mathfrak_ \mathbb (classical Lie algebras) or one of the five exceptional Lie algebras. To each finite-dimensional complex semisimple Lie algebra \mathfrak, there exists a corresponding diagram (called the Dynkin diagram) where the nodes denote the simple roots, the nodes are jointed (or not jointed) by a number of lines depending on the angles between the simple roots and the arrows are put to indicate whether the roots are longer or shorter. The Dynk ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Complex Vector Space
In mathematics and physics, a vector space (also called a linear space) is a set whose elements, often called ''vectors'', may be added together and multiplied ("scaled") by numbers called '' scalars''. Scalars are often real numbers, but can be complex numbers or, more generally, elements of any field. The operations of vector addition and scalar multiplication must satisfy certain requirements, called ''vector axioms''. The terms real vector space and complex vector space are often used to specify the nature of the scalars: real coordinate space or complex coordinate space. Vector spaces generalize Euclidean vectors, which allow modeling of physical quantities, such as forces and velocity, that have not only a magnitude, but also a direction. The concept of vector spaces is fundamental for linear algebra, together with the concept of matrix, which allows computing in vector spaces. This provides a concise and synthetic way for manipulating and studying systems of linear ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |