|
Gabor Atom
In applied mathematics, Gabor atoms, or Gabor functions, are functions used in the analysis proposed by Dennis Gabor in 1946 in which a family of functions is built from translations and modulations of a generating function. Overview In 1946, Dennis Gabor suggested the idea of using a granular system to produce sound. In his work, Gabor discussed the problems with Fourier analysis. Although he found the mathematics to be correct, it did not reflect the behaviour of sound in the world, because sounds, such as the sound of a siren, have variable frequencies over time. Another problem was the underlying supposition, as we use sine waves analysis, that the signal under concern has infinite duration even though sounds in real life have limited duration – see time–frequency analysis. Gabor applied ideas from quantum physics to sound, allowing an analogy between sound and quanta. He proposed a mathematical method to reduce Fourier analysis into cells. His research aimed at the info ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
 |
Mathematics
Mathematics is an area of knowledge that includes the topics of numbers, formulas and related structures, shapes and the spaces in which they are contained, and quantities and their changes. These topics are represented in modern mathematics with the major subdisciplines of number theory, algebra, geometry, and analysis, respectively. There is no general consensus among mathematicians about a common definition for their academic discipline. Most mathematical activity involves the discovery of properties of abstract objects and the use of pure reason to prove them. These objects consist of either abstractions from nature orin modern mathematicsentities that are stipulated to have certain properties, called axioms. A ''proof'' consists of a succession of applications of deductive rules to already established results. These results include previously proved theorems, axioms, andin case of abstraction from naturesome basic properties that are considered true starting poin ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
Function (mathematics)
In mathematics, a function from a set to a set assigns to each element of exactly one element of .; the words map, mapping, transformation, correspondence, and operator are often used synonymously. The set is called the domain of the function and the set is called the codomain of the function.Codomain ''Encyclopedia of Mathematics'Codomain. ''Encyclopedia of Mathematics''/ref> The earliest known approach to the notion of function can be traced back to works of Persian mathematicians Al-Biruni and Sharaf al-Din al-Tusi. Functions were originally the idealization of how a varying quantity depends on another quantity. For example, the position of a planet is a ''function'' of time. Historically, the concept was elaborated with the infinitesimal calculus at the end of the 17th century, and, until the 19th century, the functions that were considered were differentiable (that is, they had a high degree of regularity). The concept of a function was formalized at the end of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
 |
Dennis Gabor
Dennis Gabor ( ; hu, Gábor Dénes, ; 5 June 1900 – 9 February 1979) was a Hungarian-British electrical engineer and physicist, most notable for inventing holography, for which he later received the 1971 Nobel Prize in Physics. He obtained British citizenship in 1934, and spent most of his life in England. Life and career Gabor was born as Günszberg Dénes, into a Jewish family in Budapest, Hungary. In 1918, his family converted to Lutheranism. Dennis was the first-born son of Günszberg Bernát and Jakobovits Adél. Despite having a religious background, religion played a minor role in his later life and he considered himself agnostic. In 1902, the family received permission to change their surname from Günszberg to Gábor. He served with the Hungarian artillery in northern Italy during World War I. He began his studies in engineering at the Technical University of Budapest in 1918, later in Germany, at the Charlottenburg Technical University in Berlin, now known as t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
 |
Sound
In physics, sound is a vibration that propagates as an acoustic wave, through a transmission medium such as a gas, liquid or solid. In human physiology and psychology, sound is the ''reception'' of such waves and their ''perception'' by the brain. Only acoustic waves that have frequencies lying between about 20 Hz and 20 kHz, the audio frequency range, elicit an auditory percept in humans. In air at atmospheric pressure, these represent sound waves with wavelengths of to . Sound waves above 20 kHz are known as ultrasound and are not audible to humans. Sound waves below 20 Hz are known as infrasound. Different animal species have varying hearing ranges. Acoustics Acoustics is the interdisciplinary science that deals with the study of mechanical waves in gasses, liquids, and solids including vibration, sound, ultrasound, and infrasound. A scientist who works in the field of acoustics is an ''acoustician'', while someone working in the field of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
.png) |
Fourier Analysis
In mathematics, Fourier analysis () is the study of the way general functions may be represented or approximated by sums of simpler trigonometric functions. Fourier analysis grew from the study of Fourier series, and is named after Joseph Fourier, who showed that representing a function as a sum of trigonometric functions greatly simplifies the study of heat transfer. The subject of Fourier analysis encompasses a vast spectrum of mathematics. In the sciences and engineering, the process of decomposing a function into oscillatory components is often called Fourier analysis, while the operation of rebuilding the function from these pieces is known as Fourier synthesis. For example, determining what component frequencies are present in a musical note would involve computing the Fourier transform of a sampled musical note. One could then re-synthesize the same sound by including the frequency components as revealed in the Fourier analysis. In mathematics, the term ''Fourier a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
 |
Time–frequency Analysis
In signal processing, time–frequency analysis comprises those techniques that study a signal in both the time and frequency domains ''simultaneously,'' using various time–frequency representations. Rather than viewing a 1-dimensional signal (a function, real or complex-valued, whose domain is the real line) and some transform (another function whose domain is the real line, obtained from the original via some transform), time–frequency analysis studies a two-dimensional signal – a function whose domain is the two-dimensional real plane, obtained from the signal via a time–frequency transform. The mathematical motivation for this study is that functions and their transform representation are tightly connected, and they can be understood better by studying them jointly, as a two-dimensional object, rather than separately. A simple example is that the 4-fold periodicity of the Fourier transform – and the fact that two-fold Fourier transform reverses direction – can be in ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
 |
Quantum Physics
Quantum mechanics is a fundamental theory in physics that provides a description of the physical properties of nature at the scale of atoms and subatomic particles. It is the foundation of all quantum physics including quantum chemistry, quantum field theory, quantum technology, and quantum information science. Classical physics, the collection of theories that existed before the advent of quantum mechanics, describes many aspects of nature at an ordinary ( macroscopic) scale, but is not sufficient for describing them at small (atomic and subatomic) scales. Most theories in classical physics can be derived from quantum mechanics as an approximation valid at large (macroscopic) scale. Quantum mechanics differs from classical physics in that energy, momentum, angular momentum, and other quantities of a bound system are restricted to discrete values ( quantization); objects have characteristics of both particles and waves (wave–particle duality); and there are limit ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
Square-integrable Function
In mathematics, a square-integrable function, also called a quadratically integrable function or L^2 function or square-summable function, is a real- or complex-valued measurable function for which the integral of the square of the absolute value is finite. Thus, square-integrability on the real line (-\infty,+\infty) is defined as follows. One may also speak of quadratic integrability over bounded intervals such as ,b/math> for a \leq b. An equivalent definition is to say that the square of the function itself (rather than of its absolute value) is Lebesgue integrable. For this to be true, the integrals of the positive and negative portions of the real part must both be finite, as well as those for the imaginary part. The vector space of square integrable functions (with respect to Lebesgue measure) forms the ''Lp'' space with p=2. Among the ''Lp'' spaces, the class of square integrable functions is unique in being compatible with an inner product, which allows notio ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
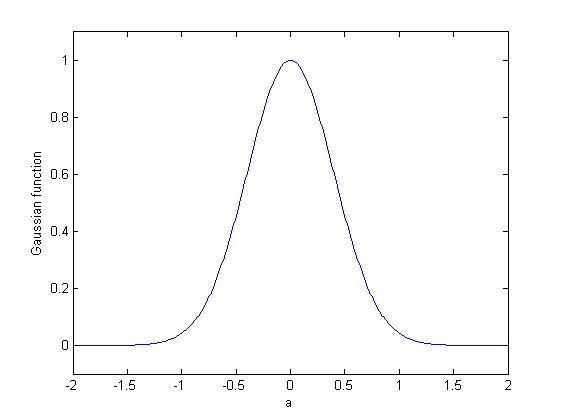 |
Gabor Transform
The Gabor transform, named after Dennis Gabor, is a special case of the short-time Fourier transform. It is used to determine the sinusoidal frequency and phase content of local sections of a signal as it changes over time. The function to be transformed is first multiplied by a Gaussian function, which can be regarded as a window function, and the resulting function is then transformed with a Fourier transform to derive the time-frequency analysis.E. Sejdić, I. Djurović, J. Jiang, “Time-frequency feature representation using energy concentration: An overview of recent advances,” ''Digital Signal Processing'', vol. 19, no. 1, pp. 153-183, January 2009. The window function means that the signal near the time being analyzed will have higher weight. The Gabor transform of a signal ''x''(''t'') is defined by this formula: : G_x(\tau,\omega) = \int_^\infty x(t)e^e^\,dt The Gaussian function has infinite range and it is impractical for implementation. However, a level of signi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
 |
Gabor Filter
In image processing, a Gabor filter, named after Dennis Gabor, is a linear filter used for texture analysis, which essentially means that it analyzes whether there is any specific frequency content in the image in specific directions in a localized region around the point or region of analysis. Frequency and orientation representations of Gabor filters are claimed by many contemporary vision scientists to be similar to those of the human visual system. They have been found to be particularly appropriate for texture representation and discrimination. In the spatial domain, a 2-D Gabor filter is a Gaussian kernel function modulated by a sinusoidal plane wave (see Gabor transform). Some authors claim that simple cells in the visual cortex of mammalian brains can be modeled by Gabor functions. Thus, image analysis with Gabor filters is thought by some to be similar to perception in the human visual system. Definition Its impulse response is defined by a sinusoidal wave (a pla ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
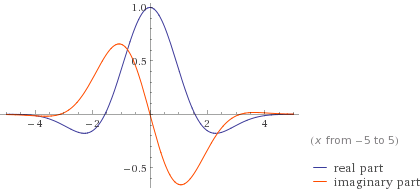 |
Gabor Wavelet
Gabor wavelets are wavelets invented by Dennis Gabor using complex functions constructed to serve as a basis for Fourier transforms in information theory applications. They are very similar to Morlet wavelets. They are also closely related to Gabor filters. The important property of the wavelet is that it minimizes the product of its standard deviations in the time and frequency domain. Put another way, the uncertainty in information carried by this wavelet is minimized. However they have the downside of being non-orthogonal, so efficient decomposition into the basis is difficult. Since their inception, various applications have appeared, from image processing to analyzing neurons in the human visual system. Minimal uncertainty property The motivation for Gabor wavelets comes from finding some function f(x) which minimizes its standard deviation in the time and frequency domains. More formally, the variance in the position domain is: : (\Delta x)^2 = \frac where f^(x) is ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
Wavelet
A wavelet is a wave-like oscillation with an amplitude that begins at zero, increases or decreases, and then returns to zero one or more times. Wavelets are termed a "brief oscillation". A taxonomy of wavelets has been established, based on the number and direction of its pulses. Wavelets are imbued with specific properties that make them useful for signal processing. For example, a wavelet could be created to have a frequency of Middle C and a short duration of roughly one tenth of a second. If this wavelet were to be convolved with a signal created from the recording of a melody, then the resulting signal would be useful for determining when the Middle C note appeared in the song. Mathematically, a wavelet correlates with a signal if a portion of the signal is similar. Correlation is at the core of many practical wavelet applications. As a mathematical tool, wavelets can be used to extract information from many different kinds of data, including but not limited to au ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |